
- •Геометрия Материалы для практических занятий
- •I курс, 2 семестр
- •Екатеринбург 2012
- •1. Программа курса
- •1. Аналитическая стереометрия
- •2. Геометрические преобразования плоскости и пространства
- •1. Лекции
- •2. Практические занятия
- •2. Материалы для практических занятий Занятие 1. Метод координат в пространстве. Уравнение плоскости
- •Занятие 2. Расстояние от точки до плоскости
- •Занятие 3. Прямая в пространстве
- •Занятие 4-5. Взаимное расположение прямых. Взаимное расположение прямых и плоскостей
- •Занятие 6. Расстояние между прямыми
- •Занятие 7-8. Решение задач элементарной геометрии координатным методом
- •Занятие 9-10. Исследование поверхности методом сечений
- •Занятие 11-13. Построение тел, ограниченных поверхностями
- •Занятие 14. Отображения, их виды. Преобразования множества. Композиция преобразований
- •Занятие 15. Параллельный перенос и поворот плоскости
- •Занятие 16. Осевая и скользящая симметрия
- •Занятие 17. Геометрические свойства движений. Аналитическое задание движения
- •Занятие 18. Подобия плоскости. Гомотетия
- •Занятие 19. Геометрические свойства аффинных преобразований
- •Занятие 20. Движения трехмерного евклидова пространства, их классификация
- •Занятие 21. Группы самосовмещений правильных многогранников
- •Занятие 22-24. Решение задач элементарной геометрии методом геометрических преобразований
- •3. Вариант контрольной работы по теме«Метод координат в пространстве»
- •4. Вариант контрольной работы по теме «Геометрические преобразования плоскости»
- •5. Вариант тестового задания для контроля остаточных знаний
- •Литература
- •Геометрия
- •620017 Екатеринбург, пр. Космонавтов, 26
Занятие 2. Расстояние от точки до плоскости
Цель занятия: Научиться применять формулу вычисления расстояния от точки до плоскости к решению задач.
Задачи
Вычислить расстояние между плоскостями
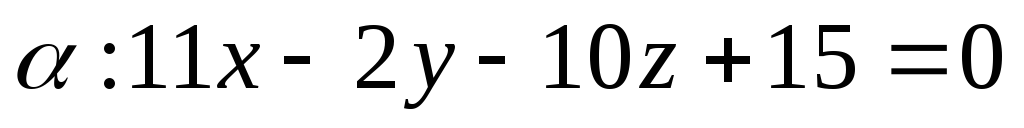 и
и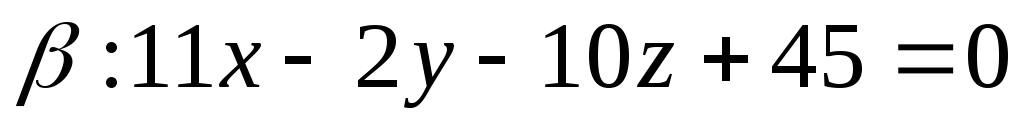 .
.На оси
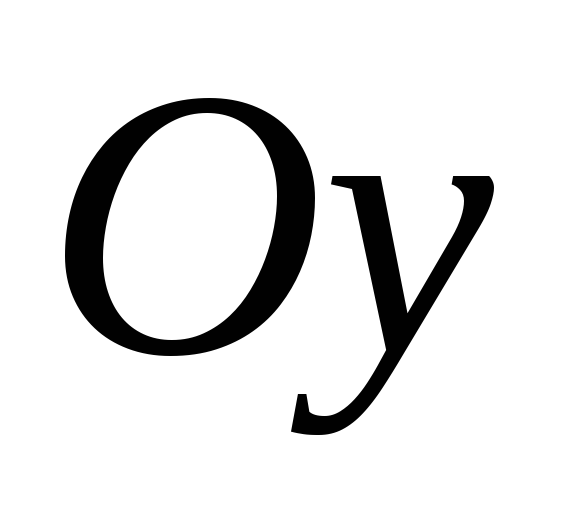 найти точку, равноудаленную от плоскостей
найти точку, равноудаленную от плоскостей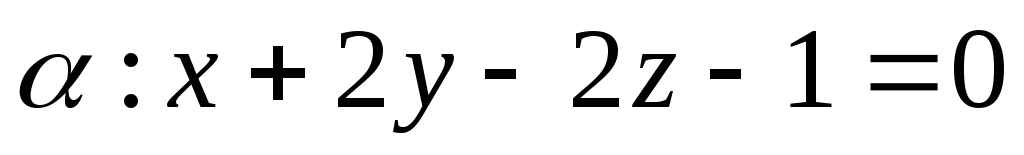 и
и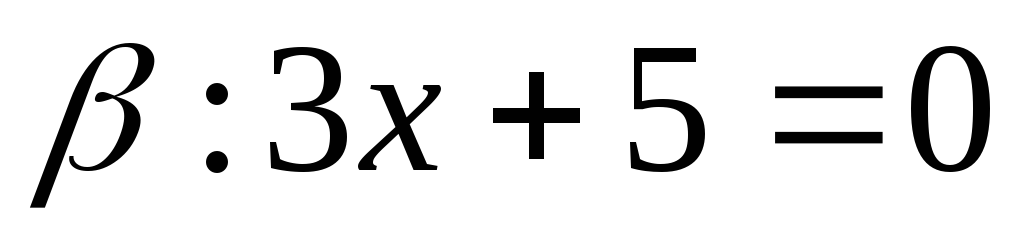 .
.К сфере
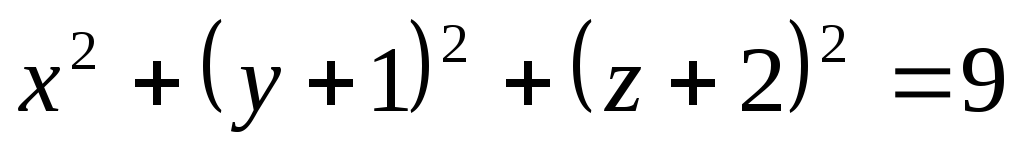 провести касательную плоскость,
параллельную плоскости
провести касательную плоскость,
параллельную плоскости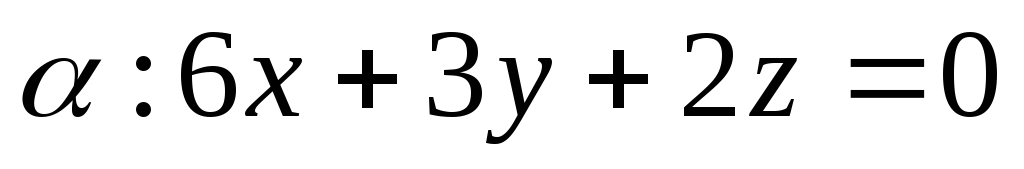 .
.Найти множество всех точек пространства, отстоящих на расстоянии 3 от плоскости
 .
.Найти уравнение биссекторной плоскости двугранного угла, образованного плоскостями
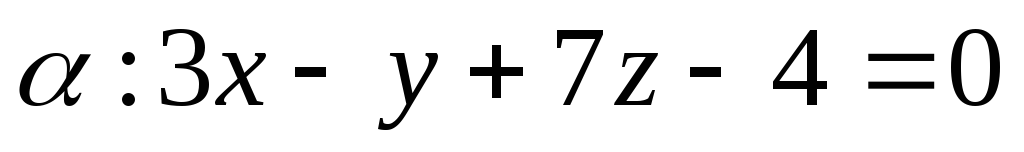 и
и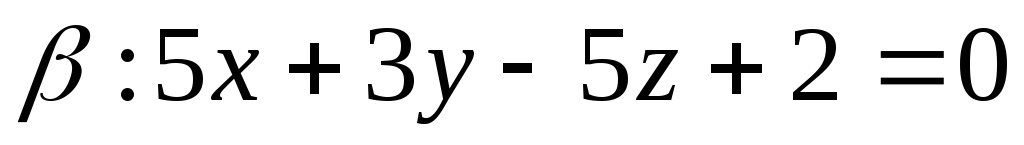 ,
в котором находится точка
,
в котором находится точка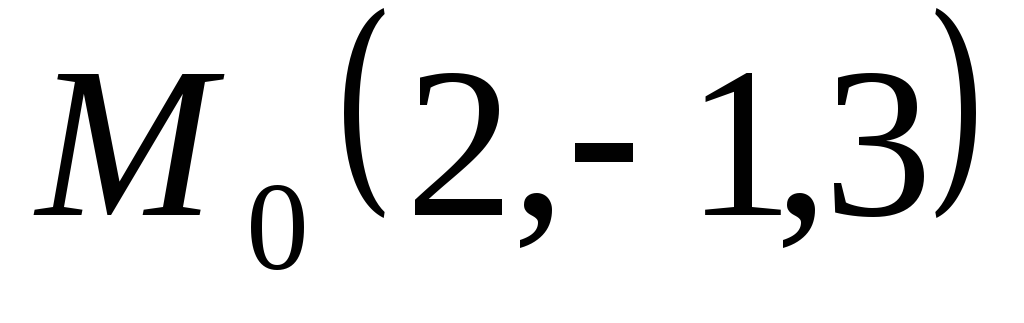 .
.Даны вершины
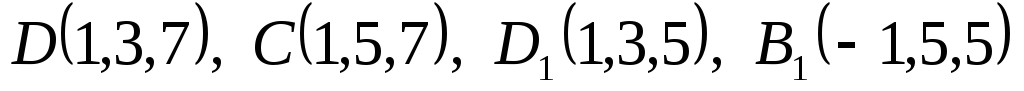 куба
куба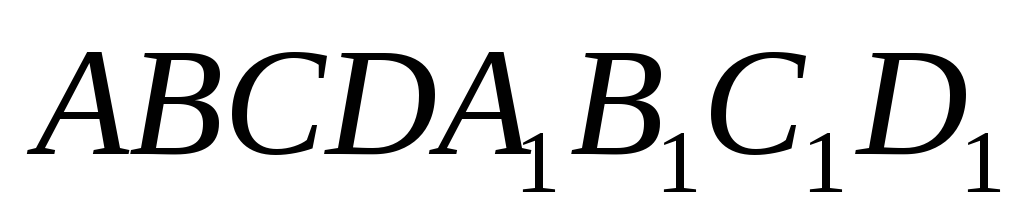 .
.
Найти: а) длину перпендикуляра, проведенного
из вершины
![]() к плоскости
к плоскости![]() ;
;
б) уравнения плоскостей, делящих пополам
двугранные углы между плоскостями
![]() и
и![]() ;
в)
уравнения плоскостей, параллельных
плоскости
;
в)
уравнения плоскостей, параллельных
плоскости![]() и отстоящих от нее на расстоянии 2.
и отстоящих от нее на расстоянии 2.
7.
Установить расположение плоскости
![]() относительно сферы
относительно сферы![]() .
.
Домашнее задание ИДЗ. Работа №3. Расстояние от точки до плоскости. [6].
Занятие 3. Прямая в пространстве
Цель занятия: Научиться составлять уравнение прямой в пространстве.
Задачи
Для прямой
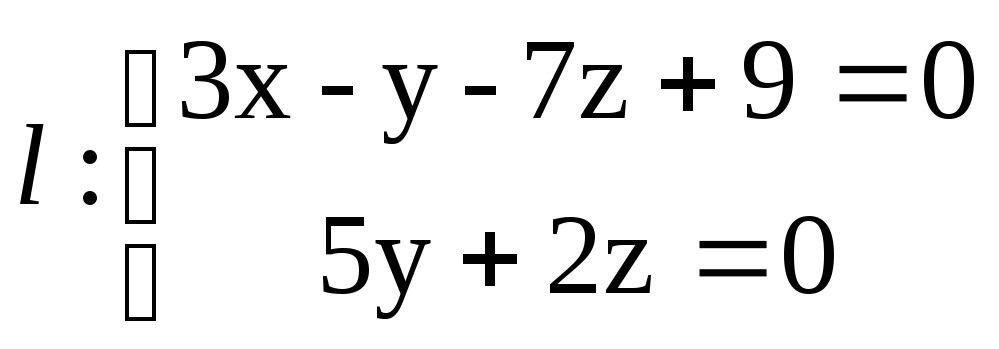 найти:
а) точку ей принадлежащую; б) направляющий
вектор; в) каноническое и параметрические
уравнения.
найти:
а) точку ей принадлежащую; б) направляющий
вектор; в) каноническое и параметрические
уравнения.Провести плоскость через точку
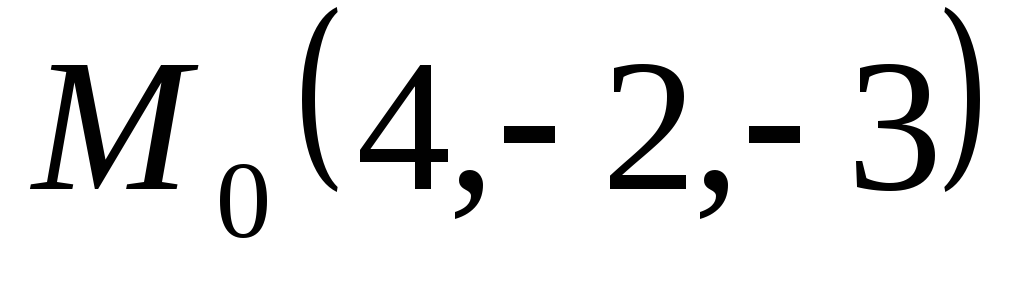 и прямую
и прямую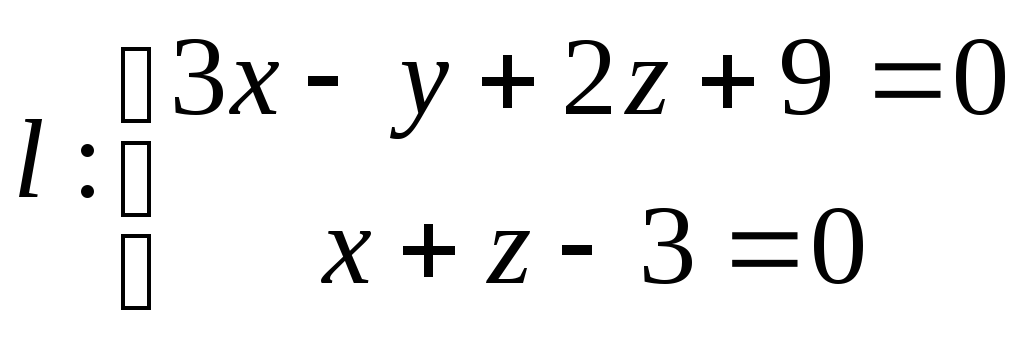 .
.Найти проекцию прямой
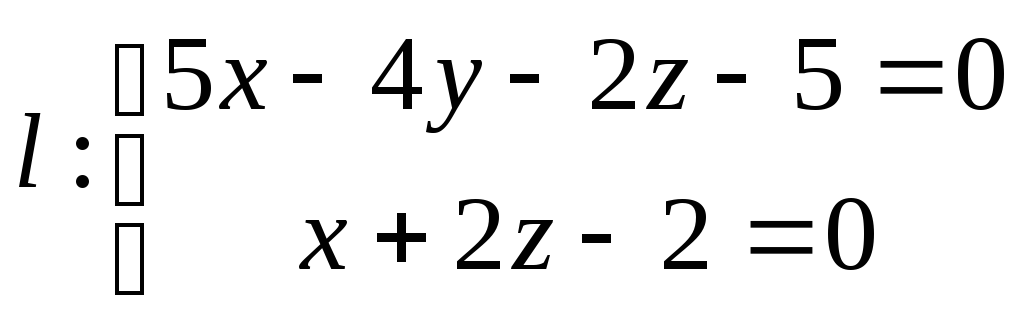 на плоскость
на плоскость .
.Найти проекцию точки
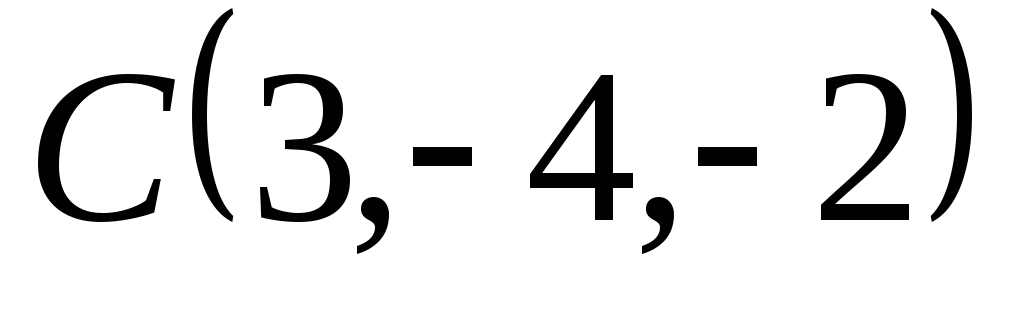 на плоскость, проходящую через прямые
на плоскость, проходящую через прямые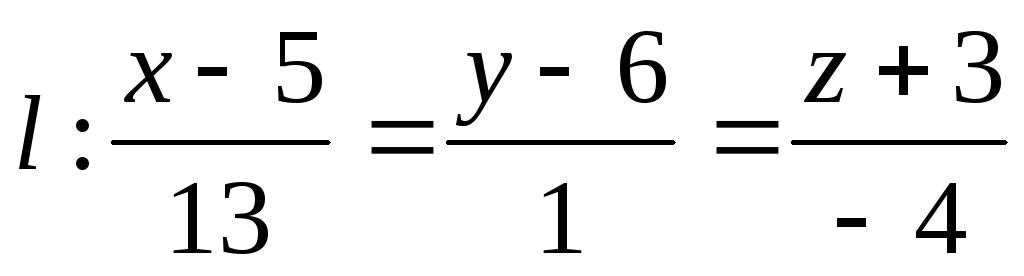 и
и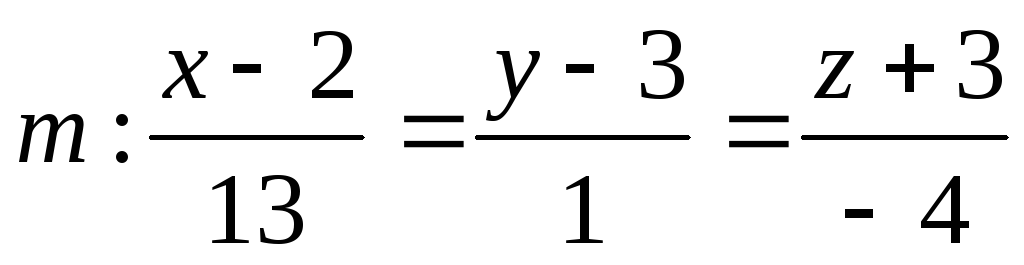 .
.Найти точку, симметричную точке
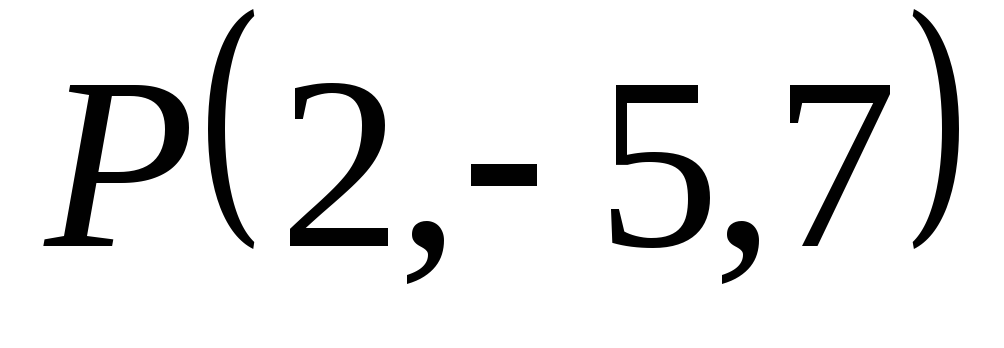 относительно прямой, проходящей через
точки
относительно прямой, проходящей через
точки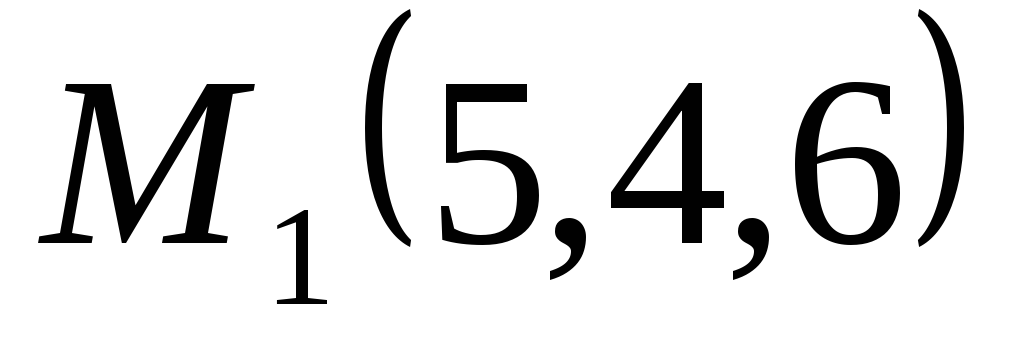 и
и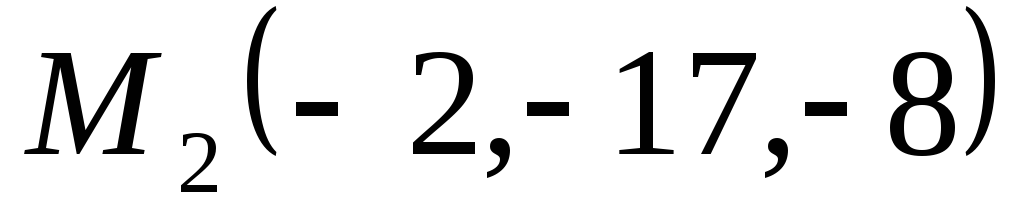 .
.
Домашнее задание [3] №1144, 1150, 1155, 1158.
Занятие 4-5. Взаимное расположение прямых. Взаимное расположение прямых и плоскостей
Цель занятия: Научиться определять взаимное расположение прямых и плоскостей в пространстве.
Задачи
Даны вершины
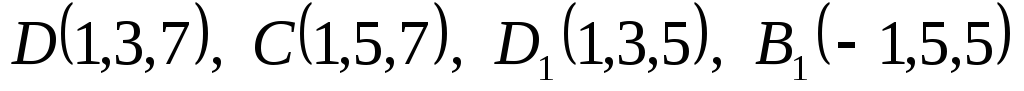 куба
куба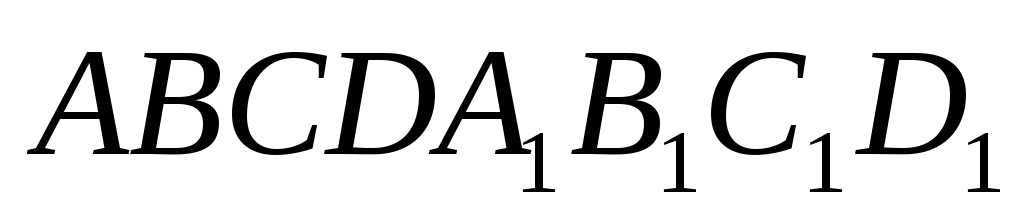 .
.
Найти:
а) общие и каноническое уравнения прямой
пересечения плоскостей
![]() и
и![]() ;
б) параметрические уравнения прямых
;
б) параметрические уравнения прямых![]() и
и![]() ;
в) канонические уравнения прямых
;
в) канонические уравнения прямых![]() и
и![]() .
.
Определить взаимное расположение прямых:
а)
![]() и
и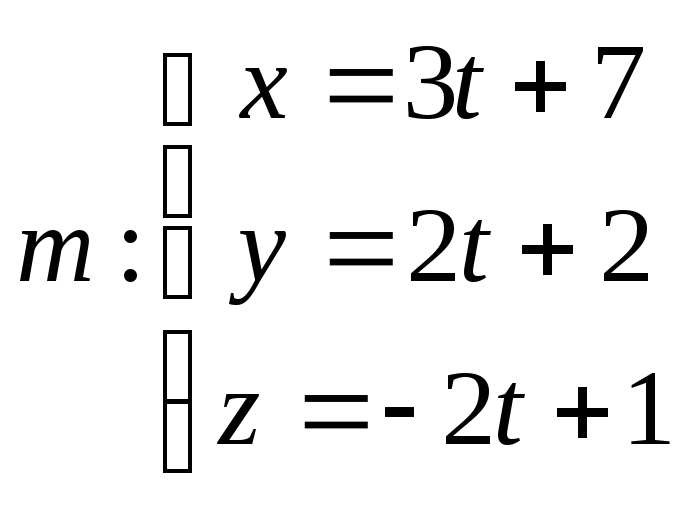 ;
;
б)
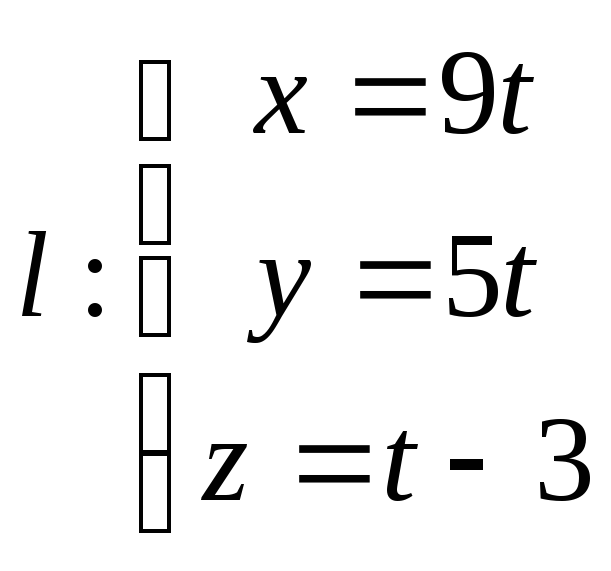 и
и![]() ;
;
в)
![]() и
и![]() .
.
Написать уравнение прямой, лежащей в плоскости
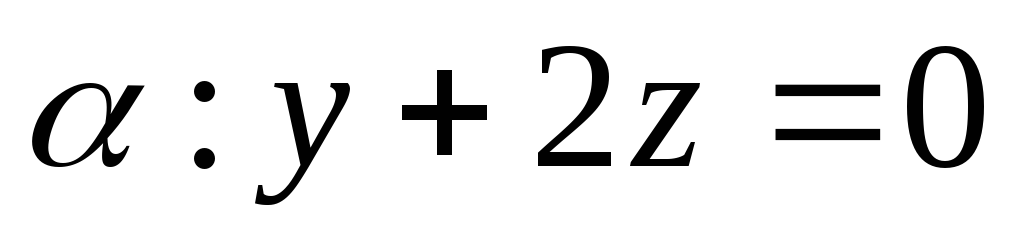 и пересекающей прямые
и пересекающей прямые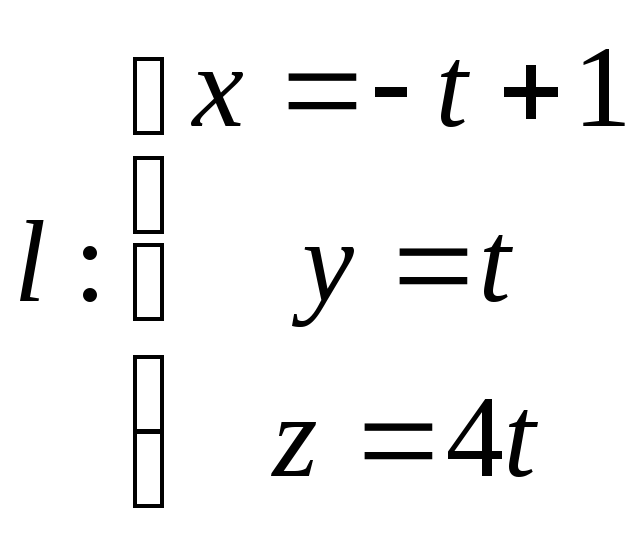 и
и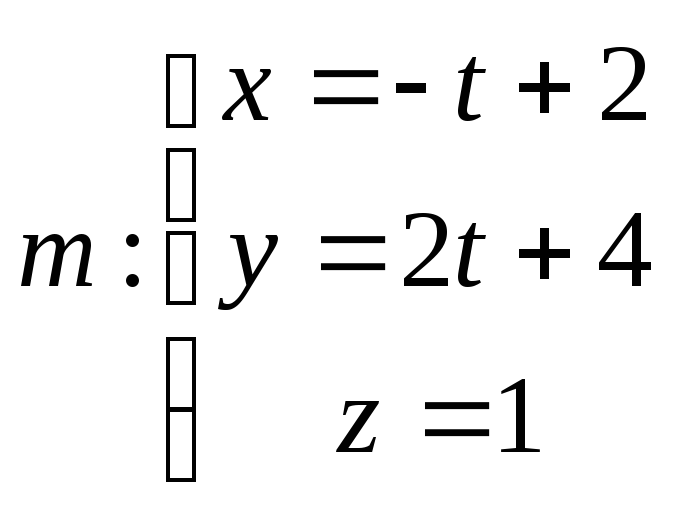 .
.Найти уравнение прямой, проходящей через точку
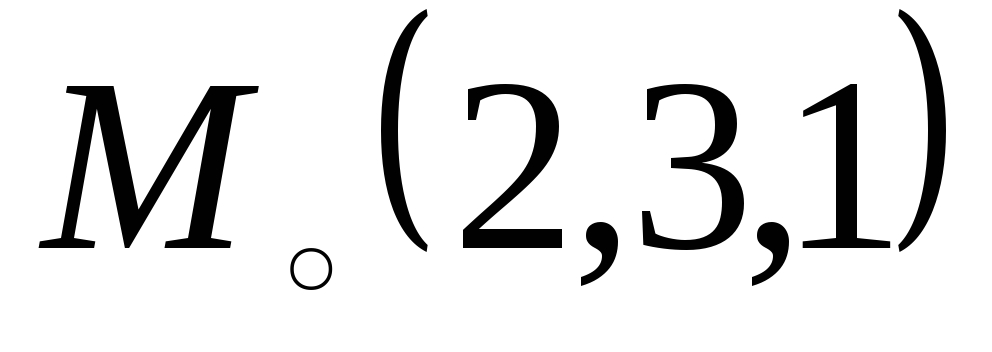 и пересекающей прямые
и пересекающей прямые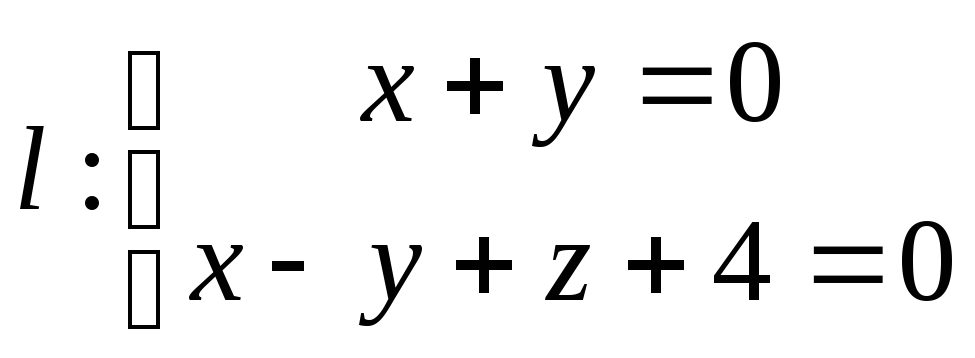 и
и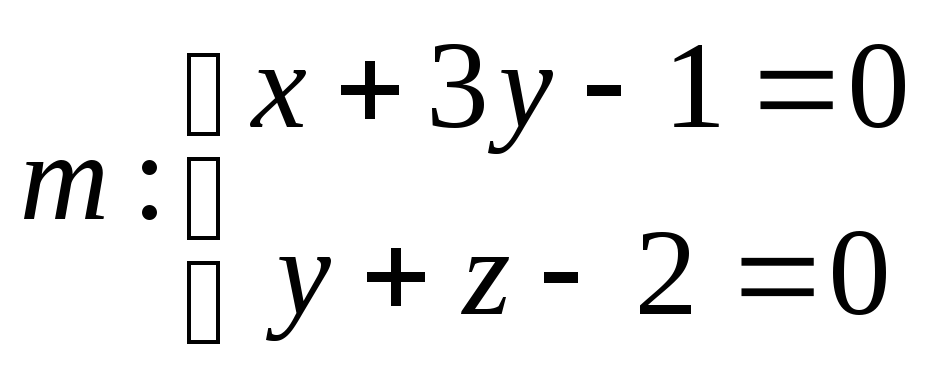 .
.Написать уравнения прямой, относительно которой симметричны прямые
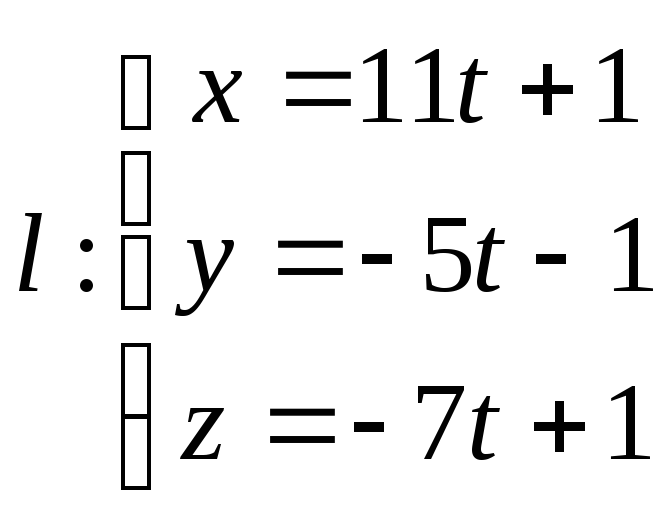 и
и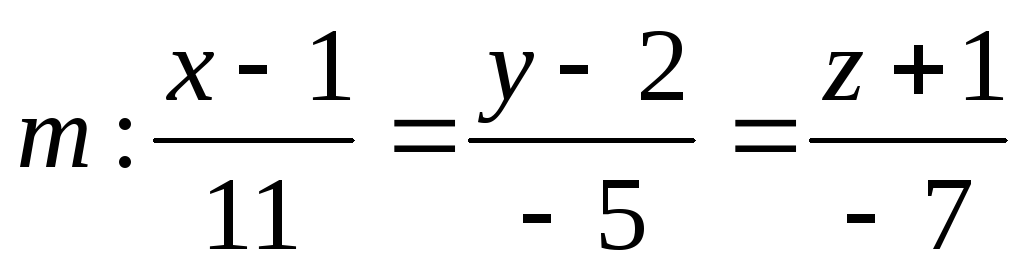 .
.Через точку
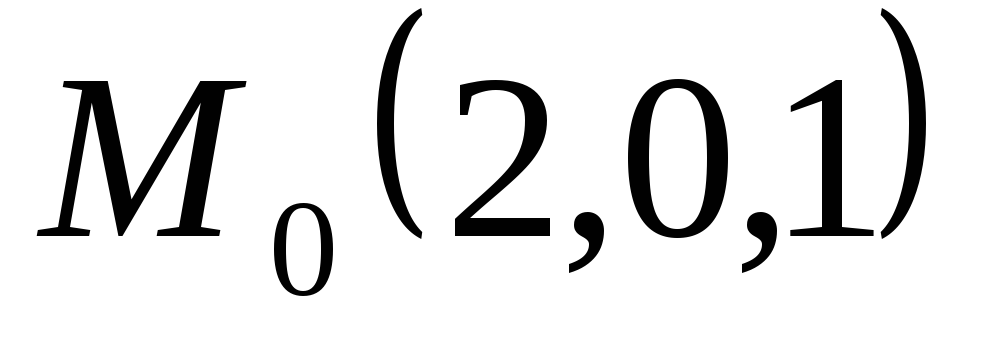 провести прямую, перпендикулярную
прямой
провести прямую, перпендикулярную
прямой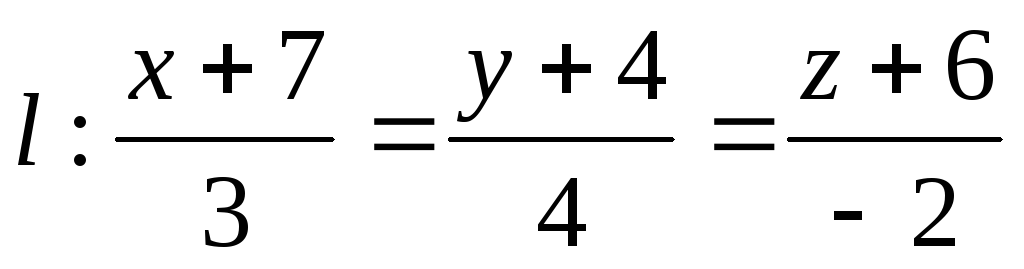 и пересекающую ее.
и пересекающую ее.
Домашнее задание ИДЗ. Работа № 4. Взаимное расположение двух прямых в пространстве. [6]
Занятие 6. Расстояние между прямыми
Цель занятия: Научиться вычислять расстояние между прямыми в пространстве.
Задачи
Даны вершины

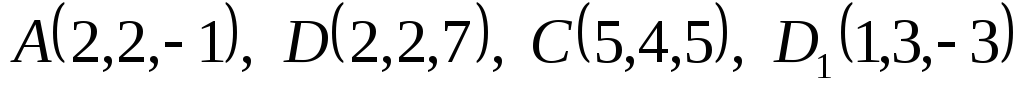 параллелепипеда
параллелепипеда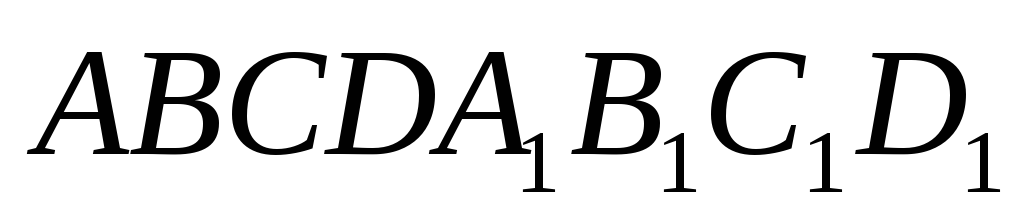 .
.
Найти: а) параметрические уравнения
прямой пересечения плоскостей
![]() и
и![]() ;
б) канонические уравнения прямых
;
б) канонические уравнения прямых![]() и
и![]() и расстояние между этими прямыми; в)
параметрические уравнения прямых
и расстояние между этими прямыми; в)
параметрические уравнения прямых![]() и
и![]() и расстояние между этими прямыми.
и расстояние между этими прямыми.
Найти расстояние от точки
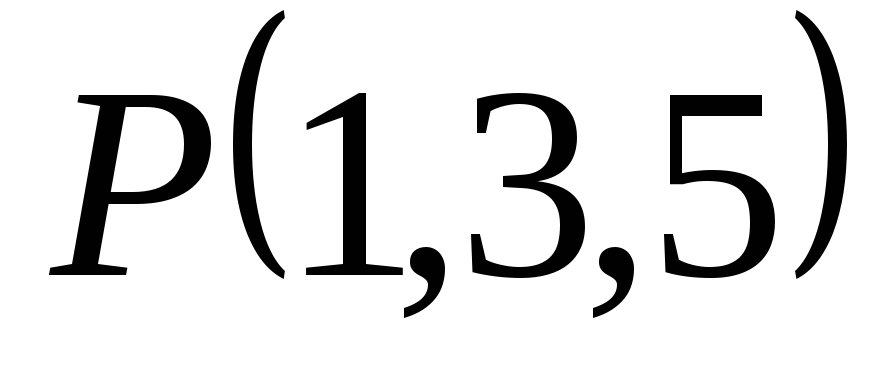 до прямой
до прямой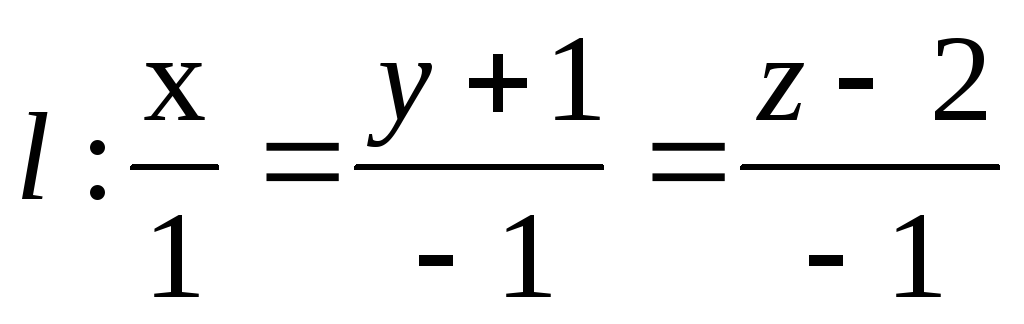 .
.Вычислить расстояние между прямыми
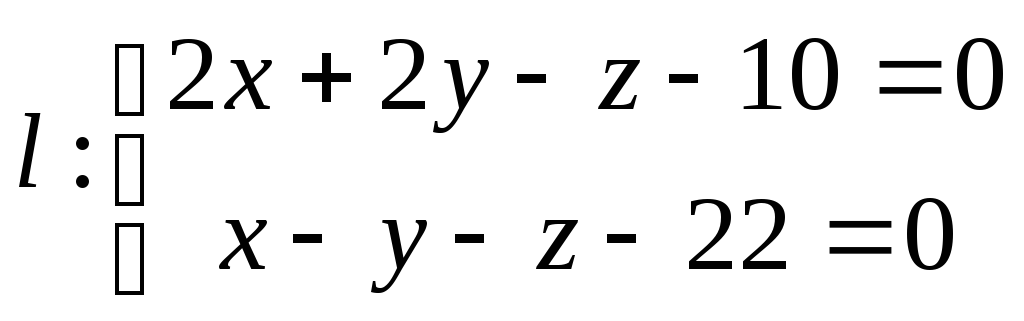 и
и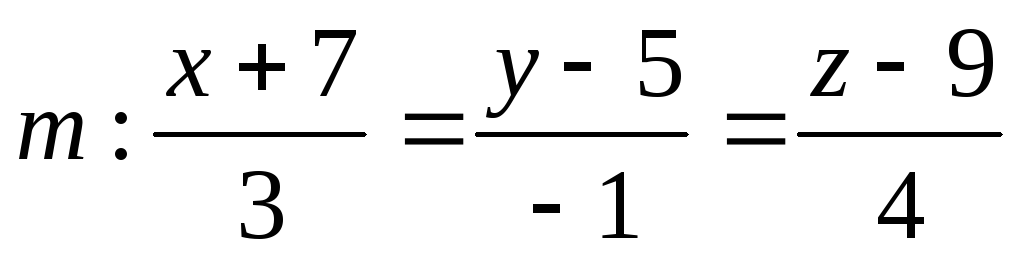 .
.Вычислить расстояние между прямыми
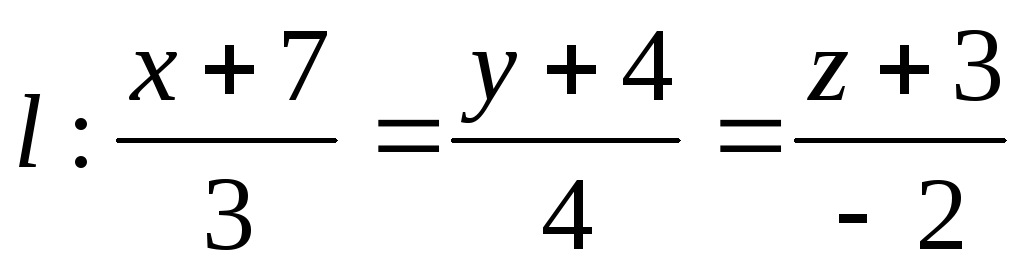 и
и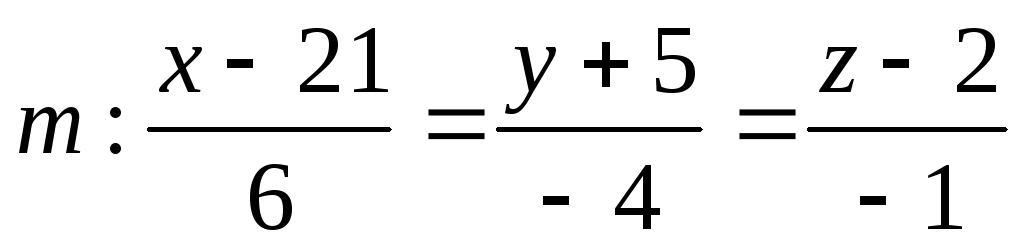 .
.
Домашнее задание ИДЗ. Работа № 1. Прямые и плоскости в пространстве. [9]
Занятие 7-8. Решение задач элементарной геометрии координатным методом
Цель занятия: Сформировать навыки применения метода координат к решению задач.
Задачи
Даны точка
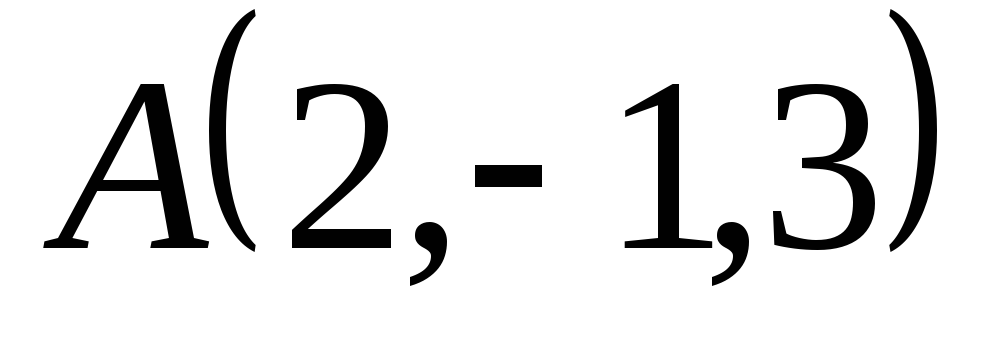 и плоскости
и плоскости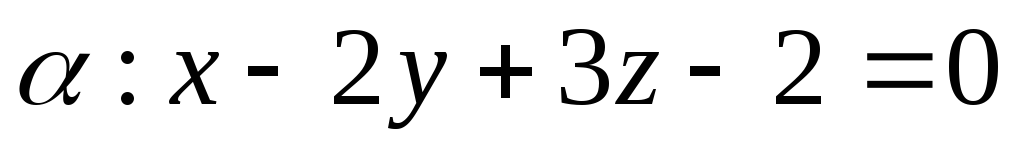 ,
,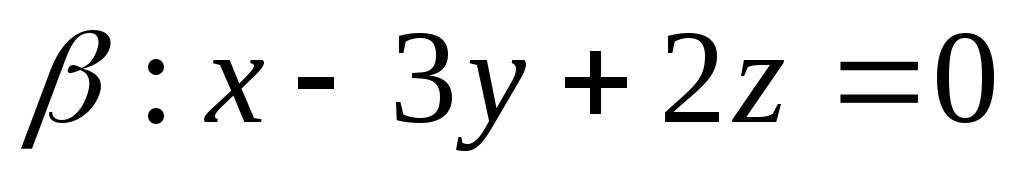 и
и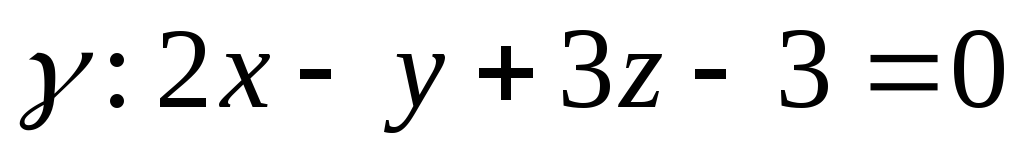 .
Не пополняя данных, сформулировать и
решить не менее семи задач на метод
координат.
.
Не пополняя данных, сформулировать и
решить не менее семи задач на метод
координат.Основанием пирамиды является равнобедренный треугольник с катетами
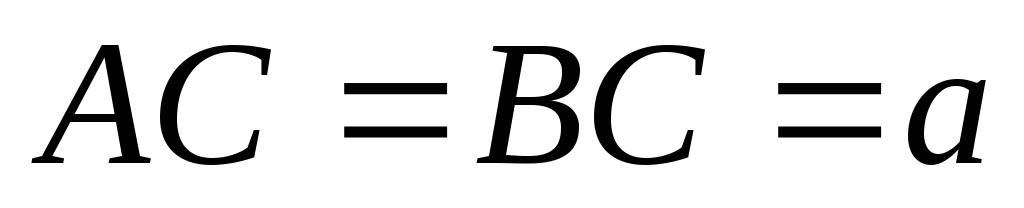 .
Боковое ребро
.
Боковое ребро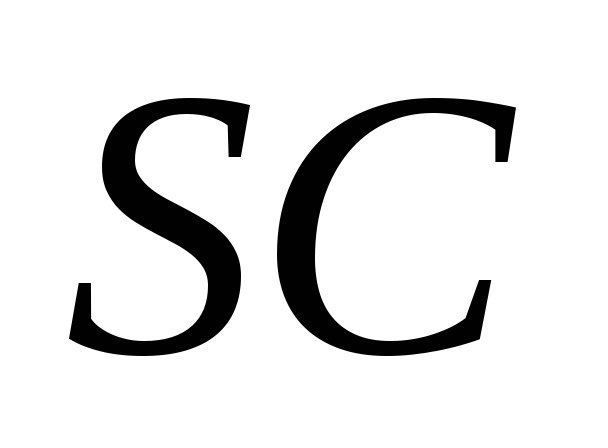 перпендикулярно плоскости основания
и равно
перпендикулярно плоскости основания
и равно .
Точка
.
Точка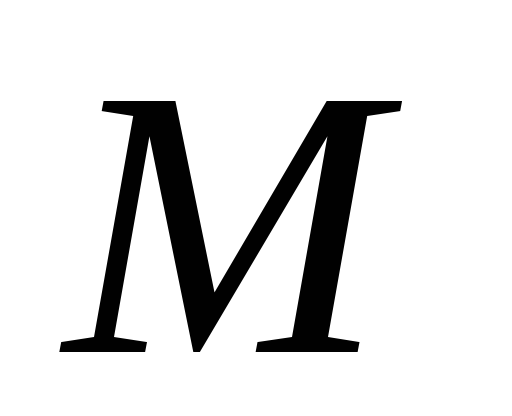 — середина ребра
— середина ребра .
Найти площадь сечения пирамиды
плоскостью, перпендикулярной прямой
.
Найти площадь сечения пирамиды
плоскостью, перпендикулярной прямой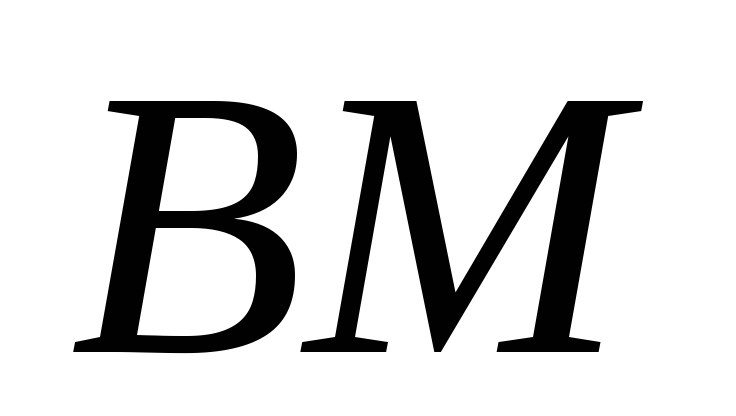 и проходящей через середину ребра
и проходящей через середину ребра .
.Найти множество всех точек пространства, равноудаленных от данной точки и данной плоскости.
Ребра куба
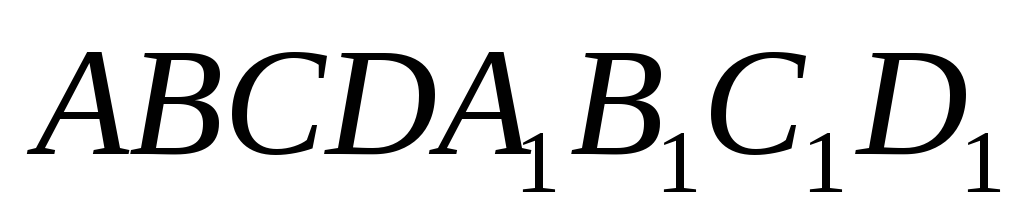 равны
равны ,
,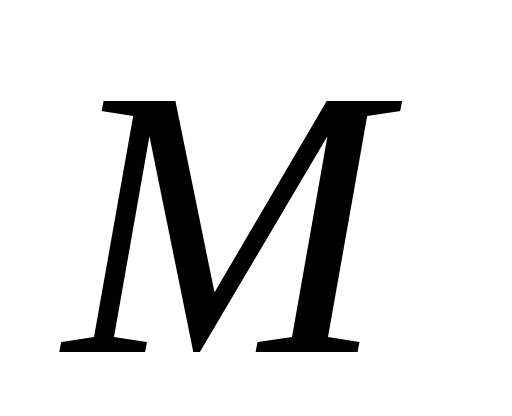 — середина ребра
— середина ребра .
Найти площадь сечения куба плоскостью,
перпендикулярной прямой
.
Найти площадь сечения куба плоскостью,
перпендикулярной прямой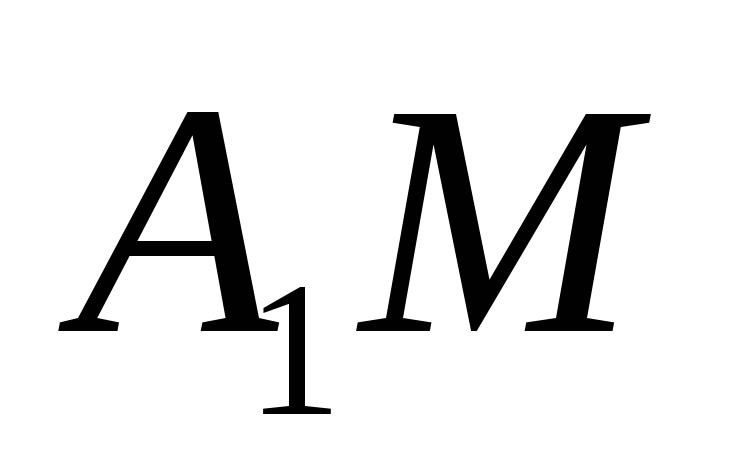 и проходящей через точку
и проходящей через точку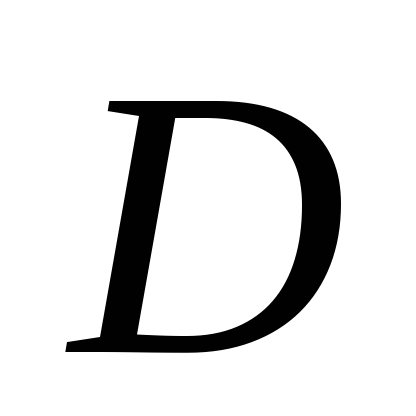 .
.Найти множество всех точек пространства, расстояние от которых до данной точки вдвое меньше расстояния до данной плоскости.
В пирамиде
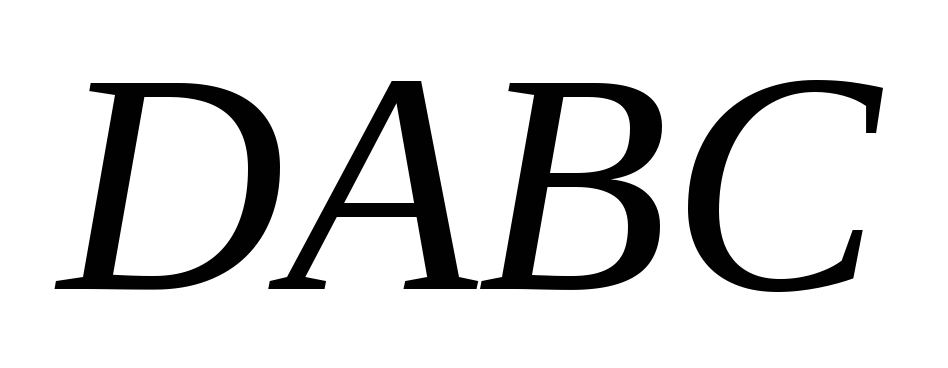 ребро
ребро является её высотой,
является её высотой,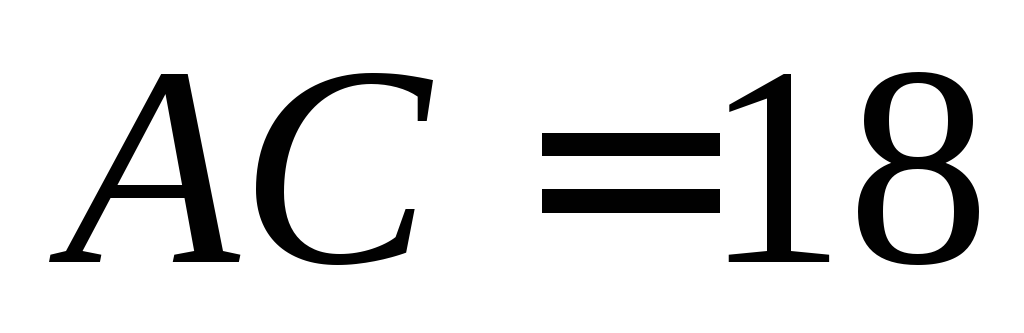 ,
,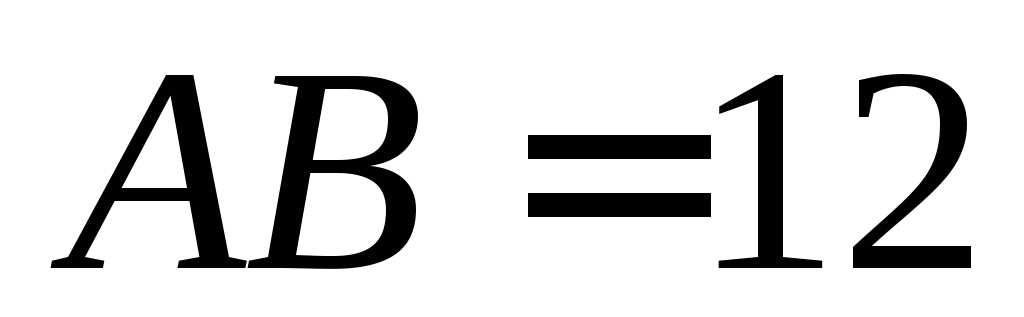 ,
,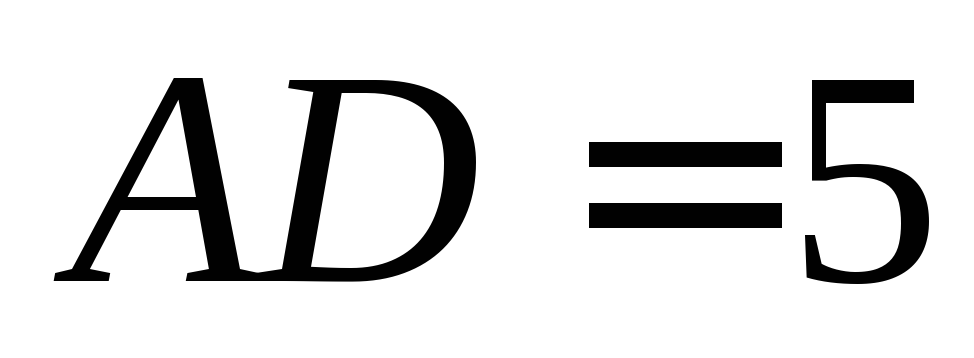 ,
,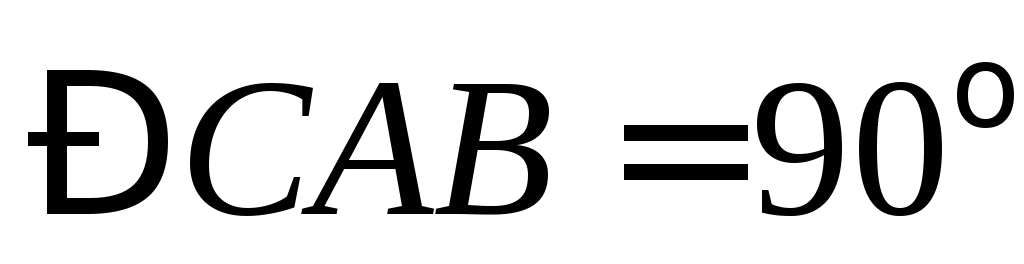 .
Найти медиану
.
Найти медиану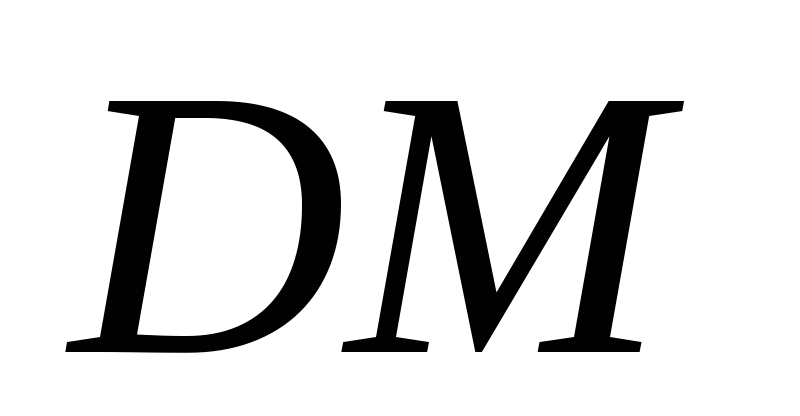 грани
грани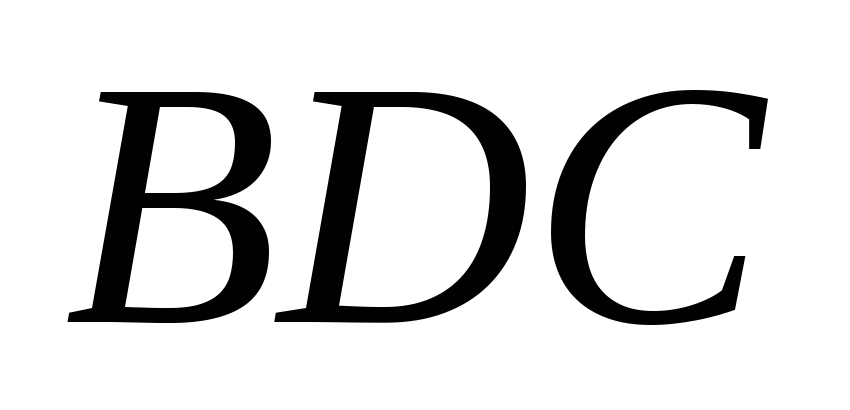 и расстояние от точки
и расстояние от точки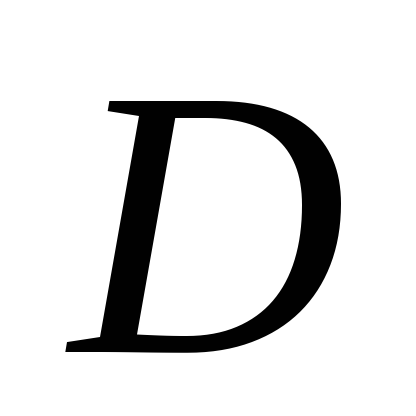 до центра тяжести грани
до центра тяжести грани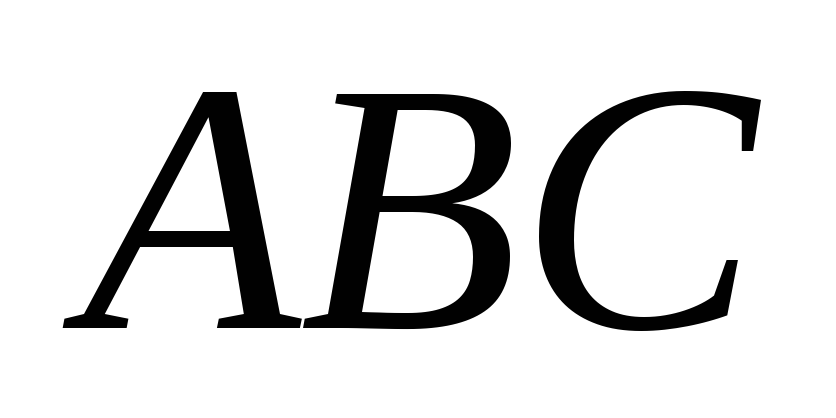 .
.В пирамиде
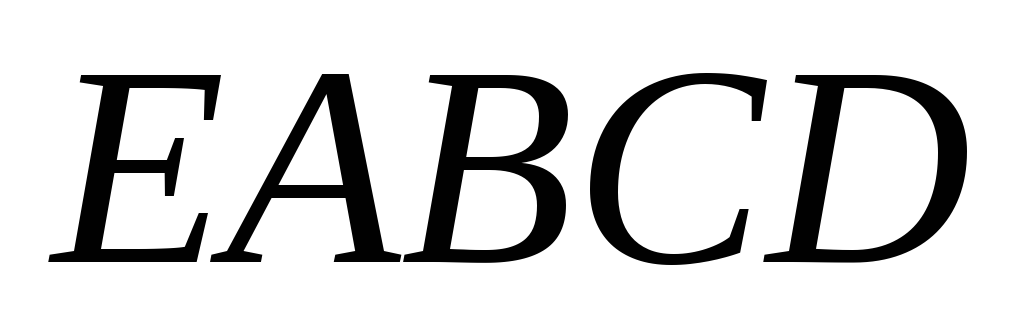
 является её высотой. Четырехугольник
является её высотой. Четырехугольник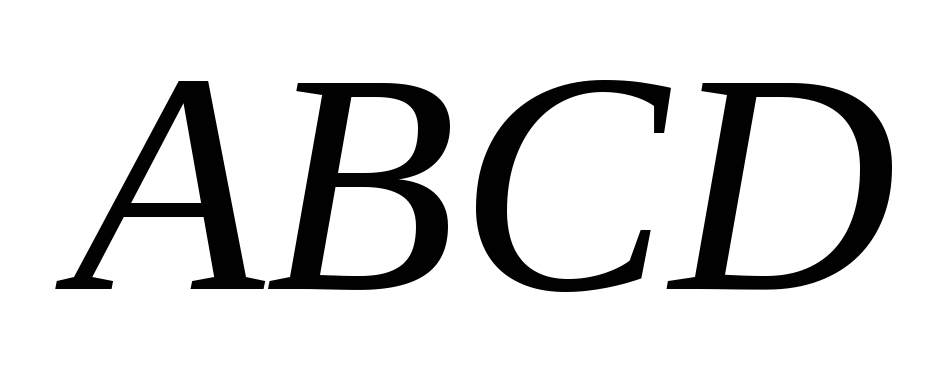 – трапеция,
– трапеция,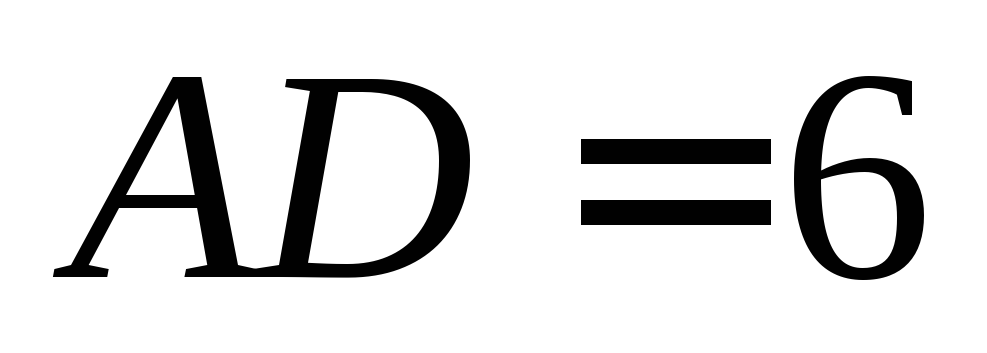 ,
,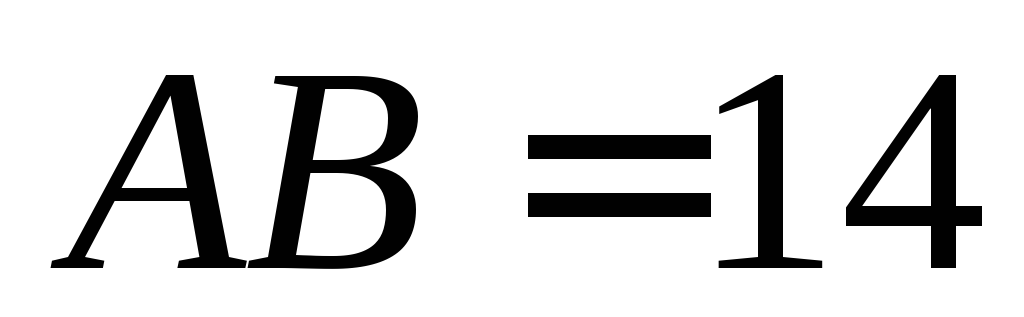 ,
,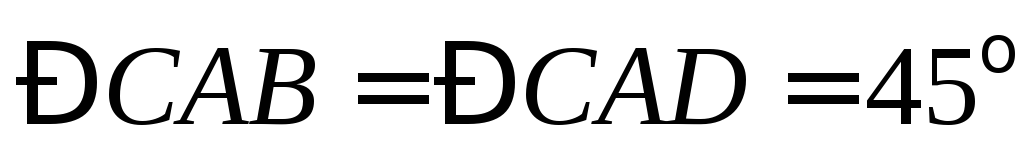 .
Найти медиану
.
Найти медиану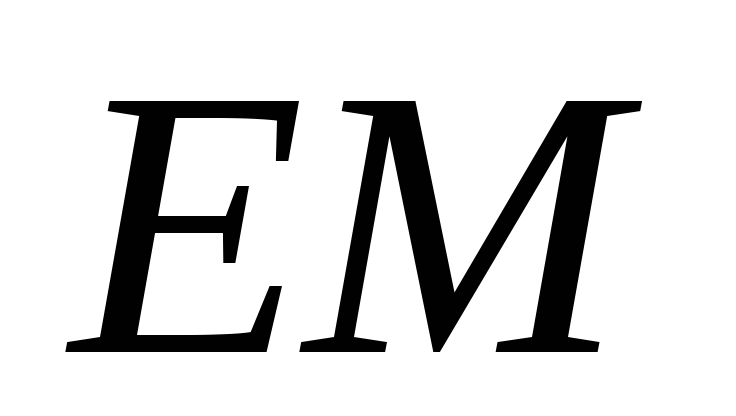 грани
грани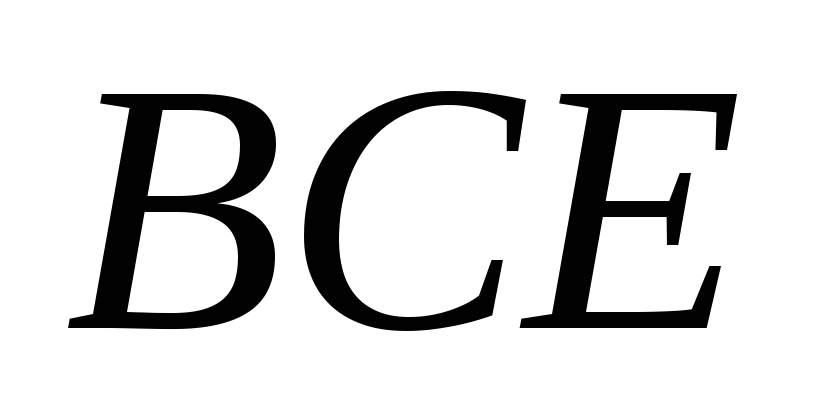 и расстояние от точки
и расстояние от точки до центра тяжести грани
до центра тяжести грани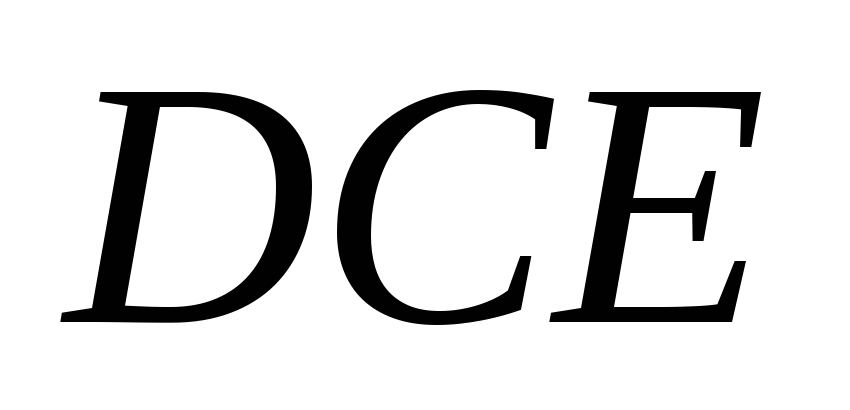 .
.В основании прямой призмы
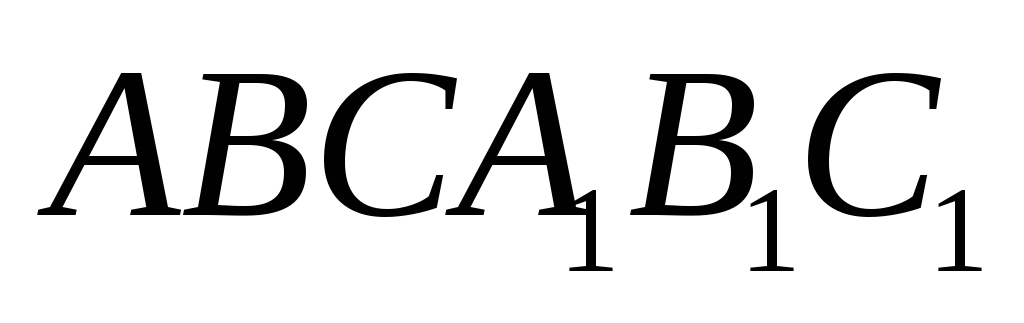 лежит треугольник с прямым углом
лежит треугольник с прямым углом .
Точки
.
Точки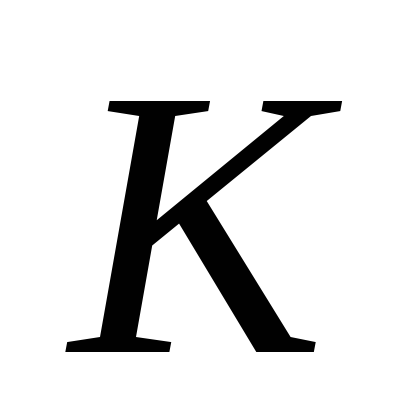 и
и – середины ребер
– середины ребер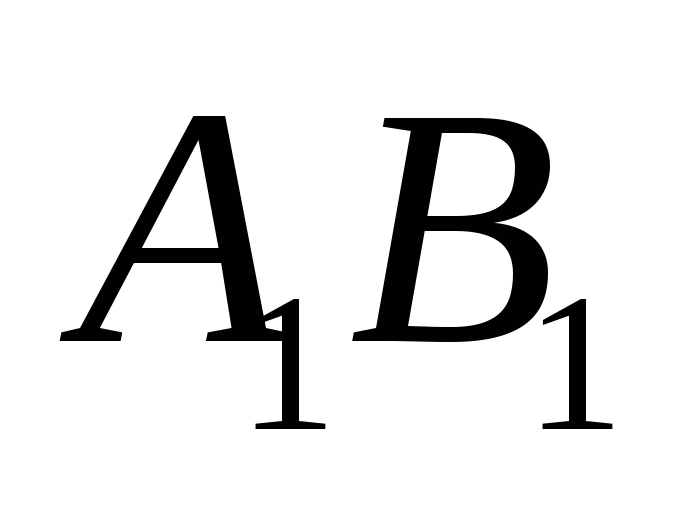 и
и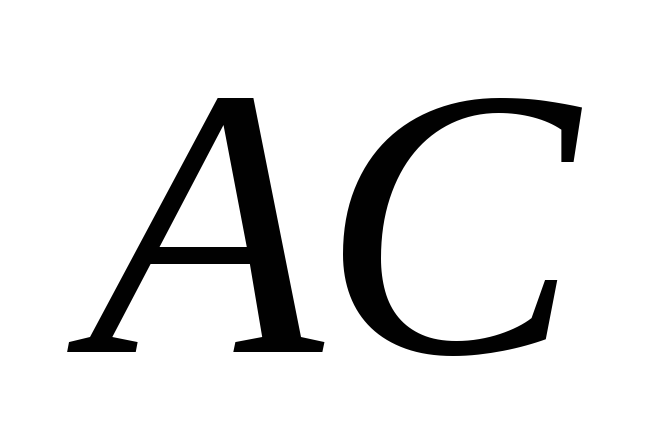 соответственно,
соответственно,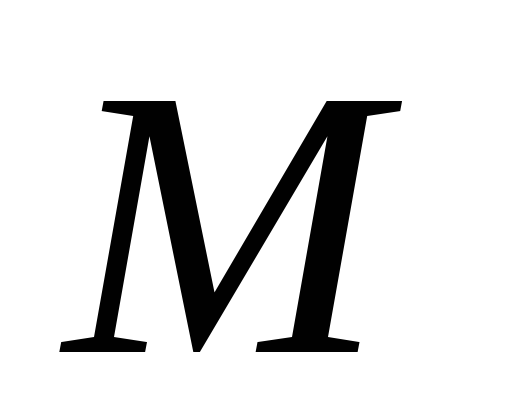 – точка пересечения диагоналей грани
– точка пересечения диагоналей грани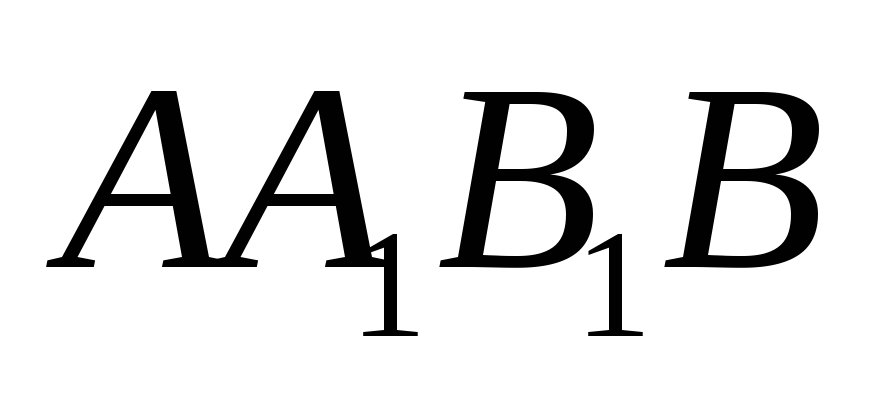 .
Точка
.
Точка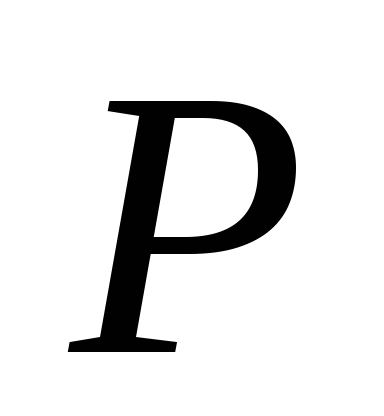 делит отрезок
делит отрезок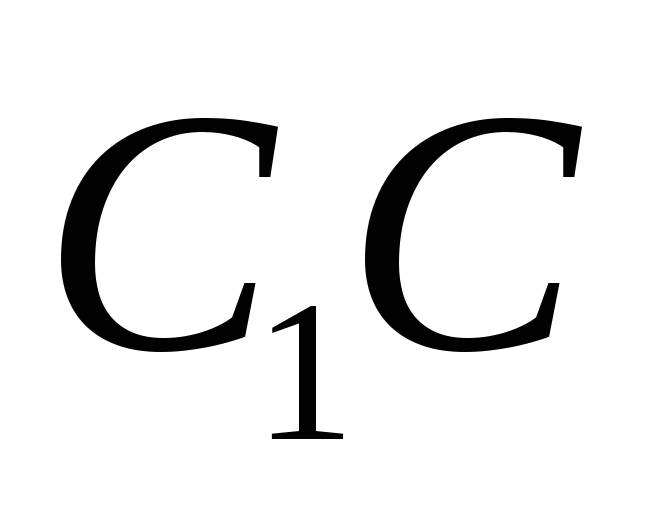 в отношении
в отношении ,
считая от вершины
,
считая от вершины .
Доказать, что прямые
.
Доказать, что прямые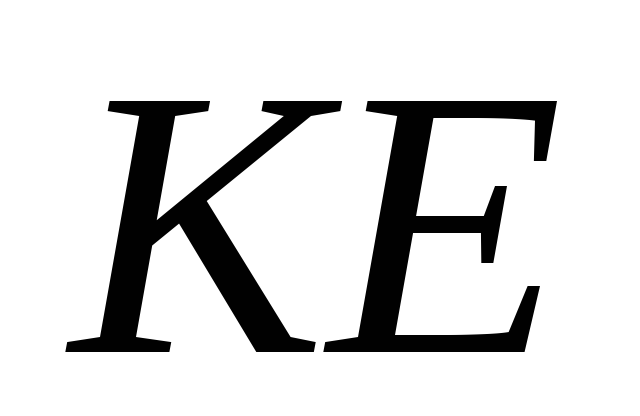 и
и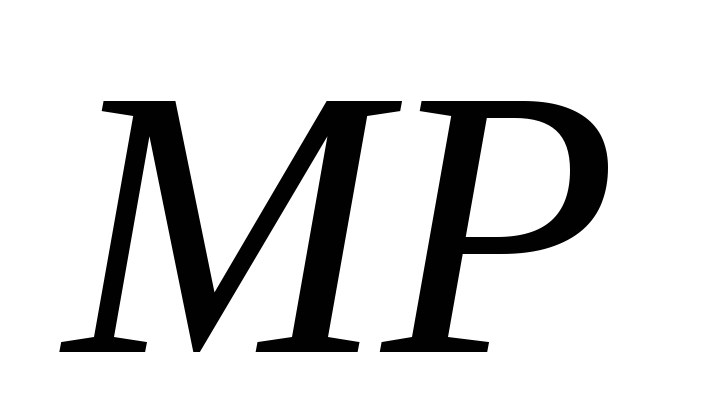 скрещиваются.
скрещиваются.Решить уравнения
![]() ;
;
![]()
В основании прямой призмы
 лежит прямоугольный равнобедренный
треугольник с катетом 1. Одна боковая
грань – квадрат.
лежит прямоугольный равнобедренный
треугольник с катетом 1. Одна боковая
грань – квадрат.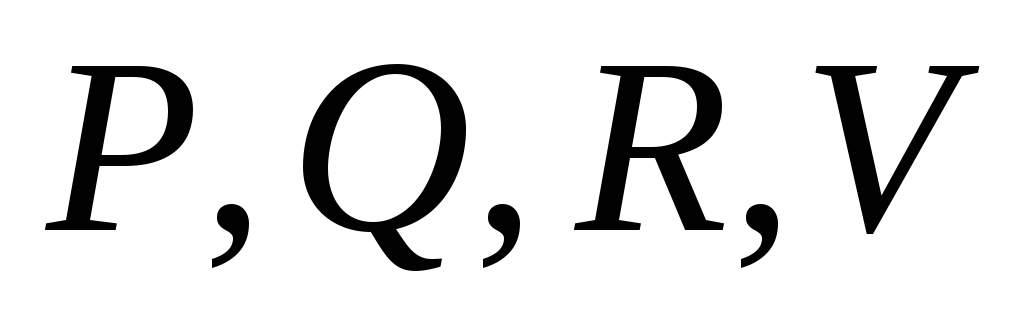 – середины
– середины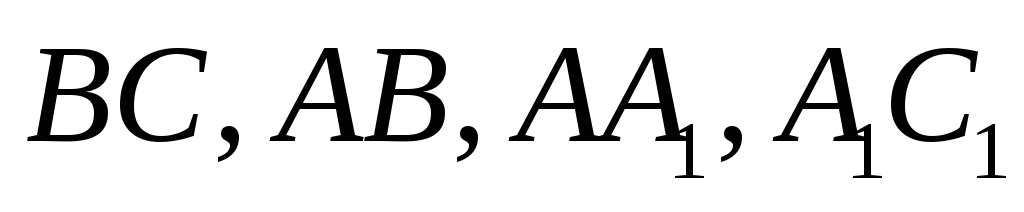 .
Найти точку, равноудаленную от а)
.
Найти точку, равноудаленную от а)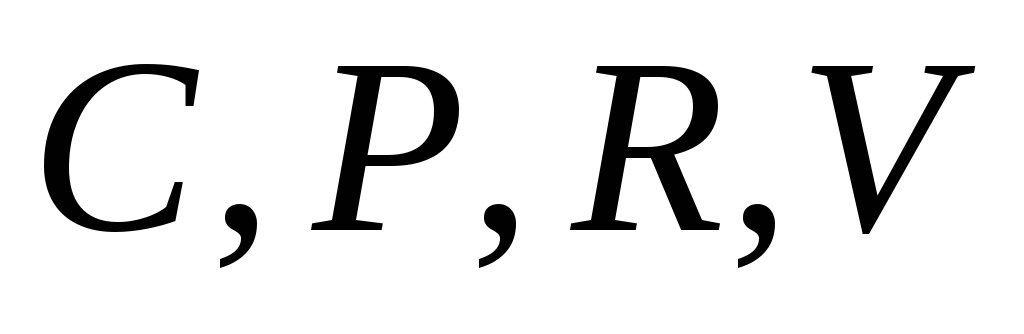 ;
б)
;
б) ;
в)
;
в)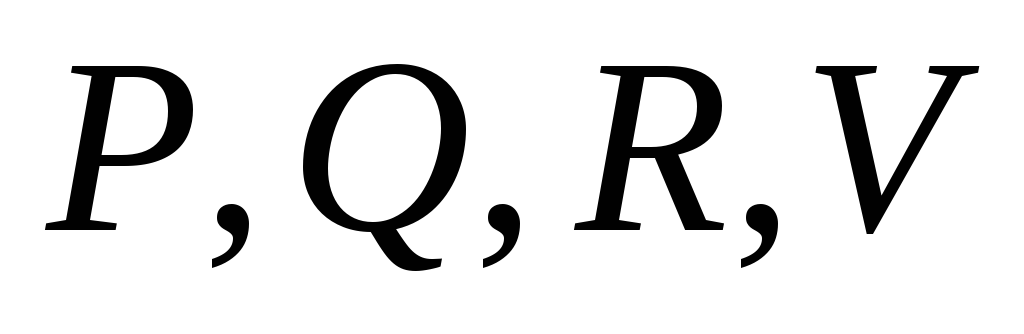 .
.Основанием прямой призмы
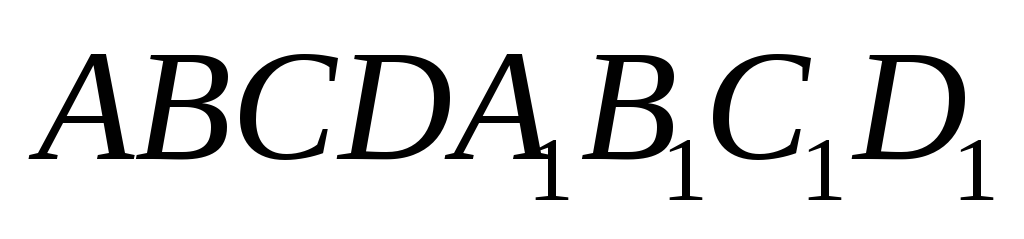 является прямоугольная трапеция,
основание
является прямоугольная трапеция,
основание которой равно боковой стороне
которой равно боковой стороне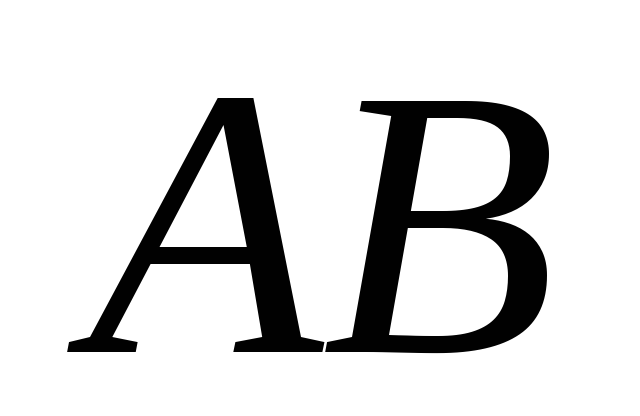 и боковому ребру призмы, а основание
и боковому ребру призмы, а основание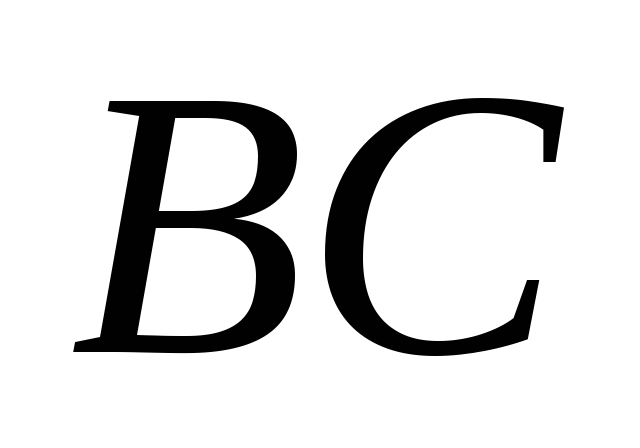 равно
равно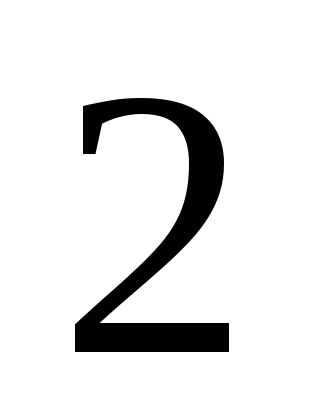 .
На сторонах
.
На сторонах и
и взяты середины
взяты середины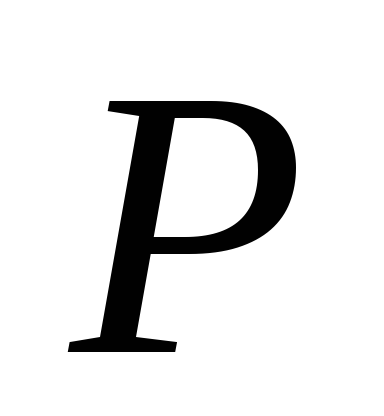 и
и .
Считая
.
Считая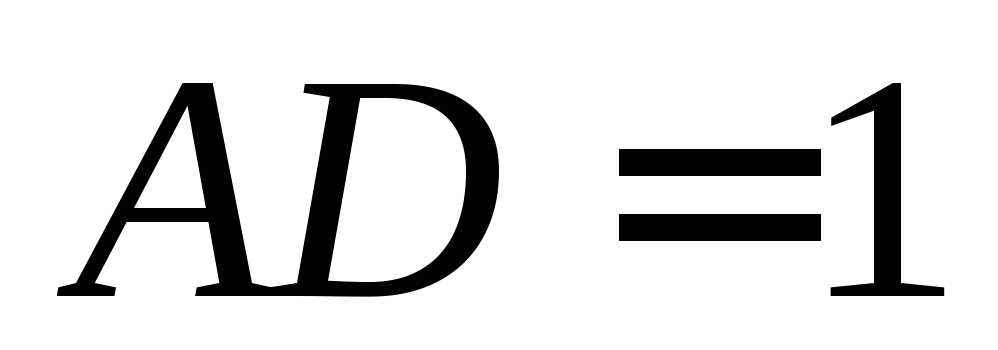 ,
найти расстояние от
,
найти расстояние от до а)
до а)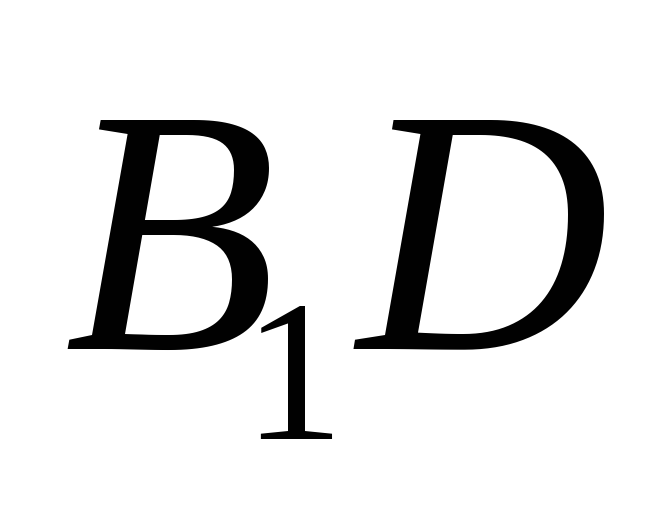 ;
б)
;
б)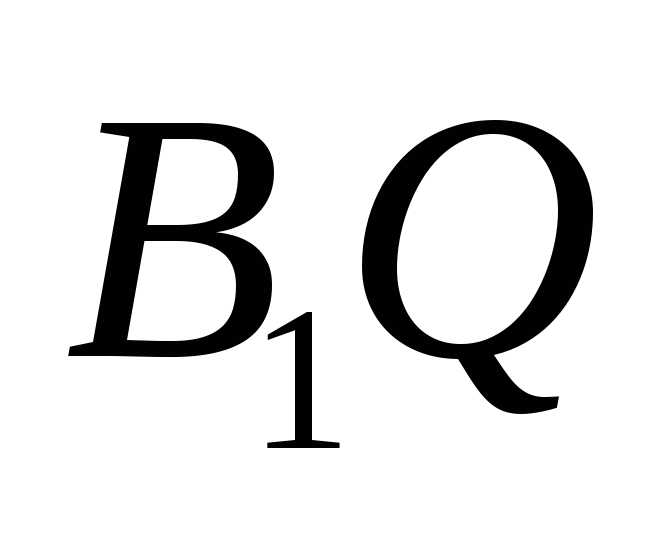 ;
в)
;
в)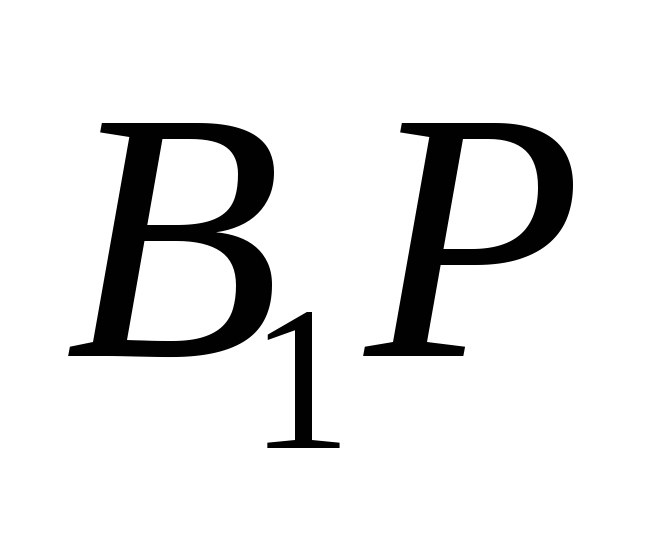 .
. – пирамида.
– пирамида.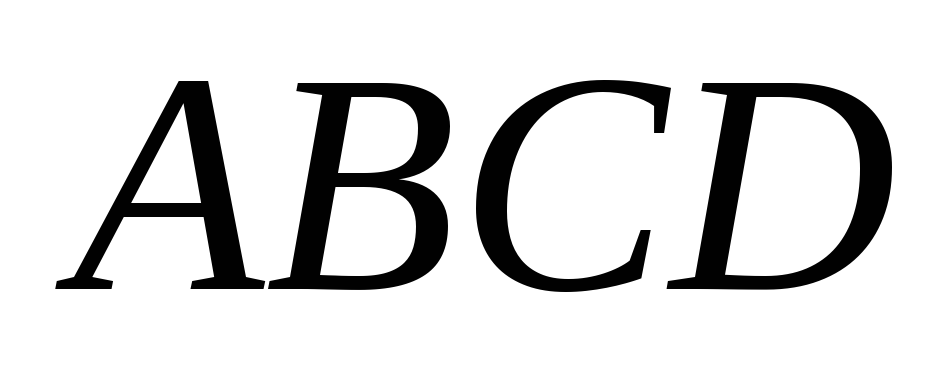 – прямоугольник.
– прямоугольник. .
.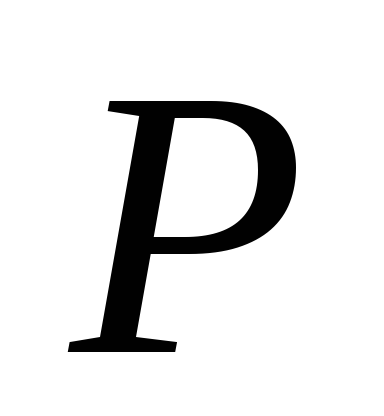 – середина
– середина ,
,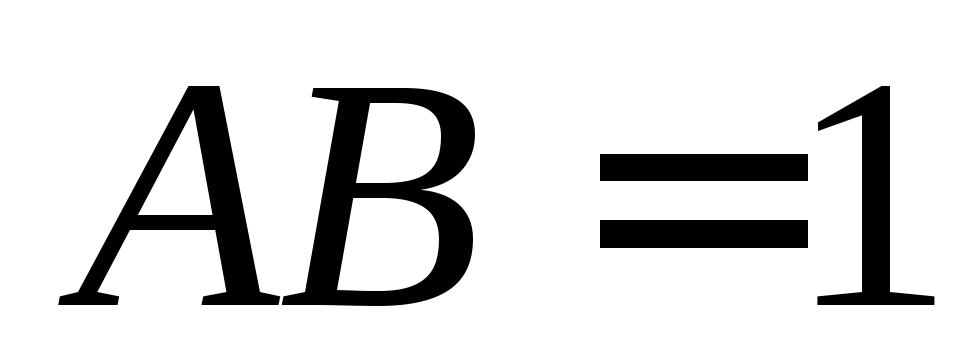 ,
,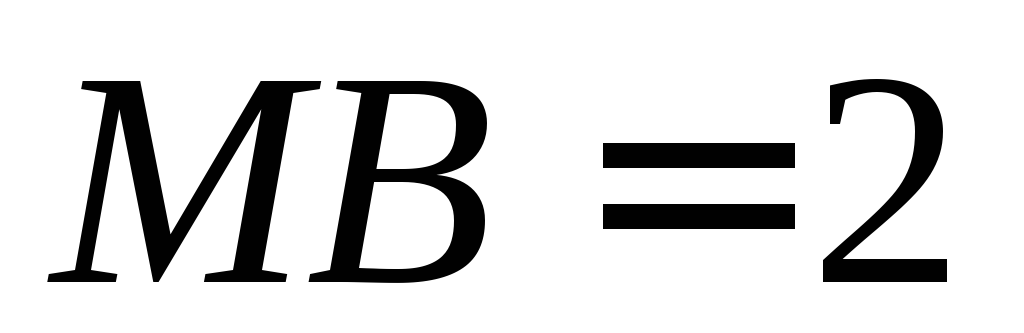 ,
,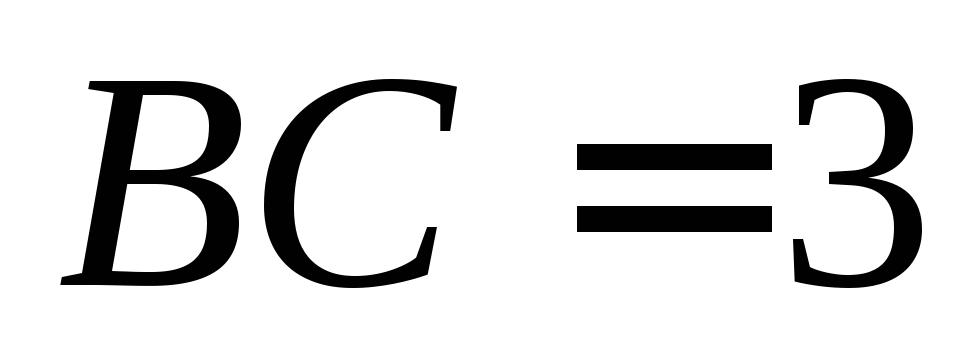 .
Найти расстояние от
.
Найти расстояние от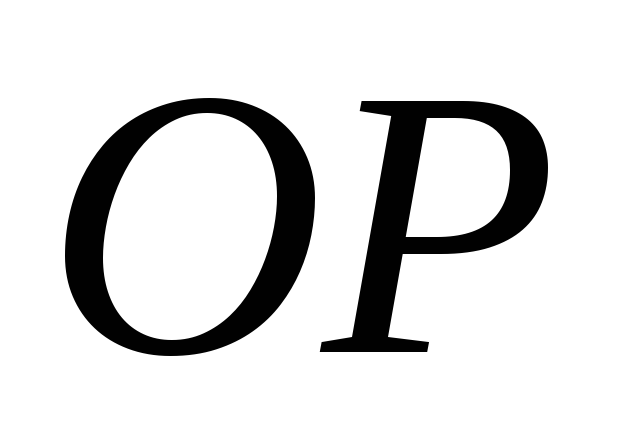 до а)
до а)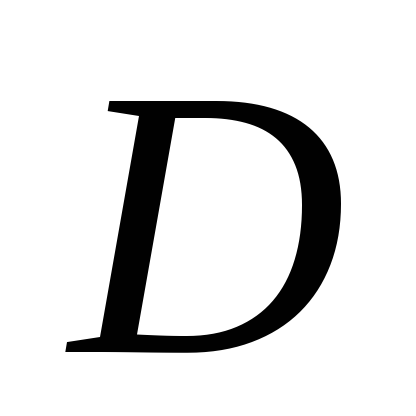 ;
б)
;
б)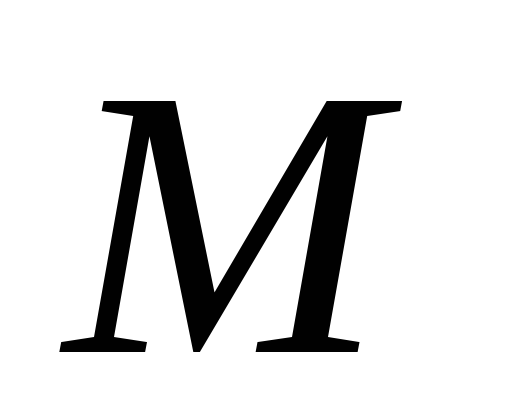 ;
в)
;
в) ,
где
,
где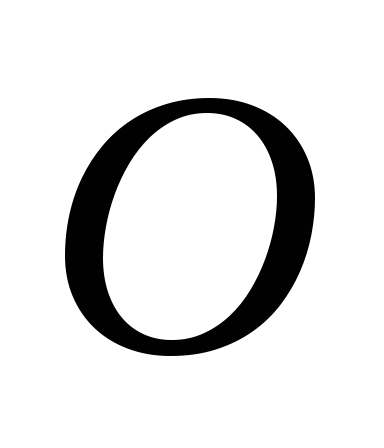 – точка пересечения диагоналей основания
пирамиды.
– точка пересечения диагоналей основания
пирамиды.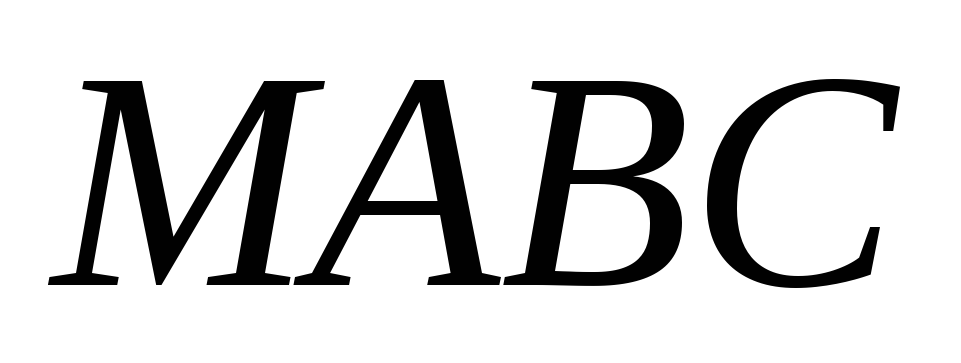 – правильная пирамида, все плоские
углы при вершине
– правильная пирамида, все плоские
углы при вершине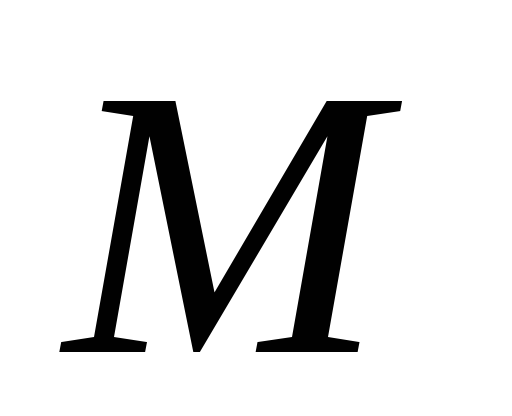 прямые. Точки
прямые. Точки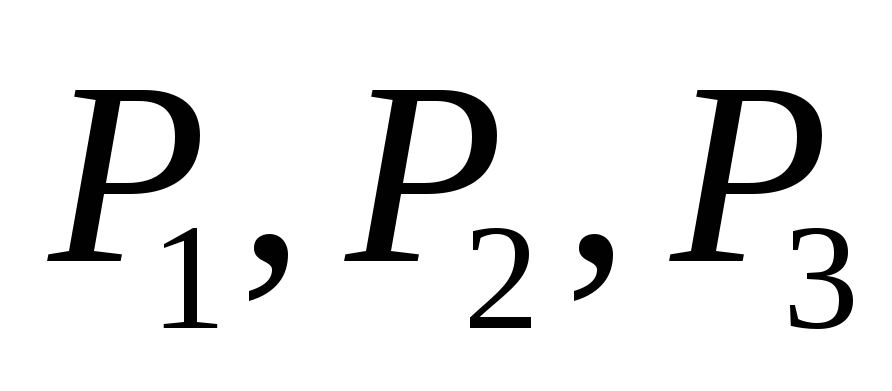 делят отрезок
делят отрезок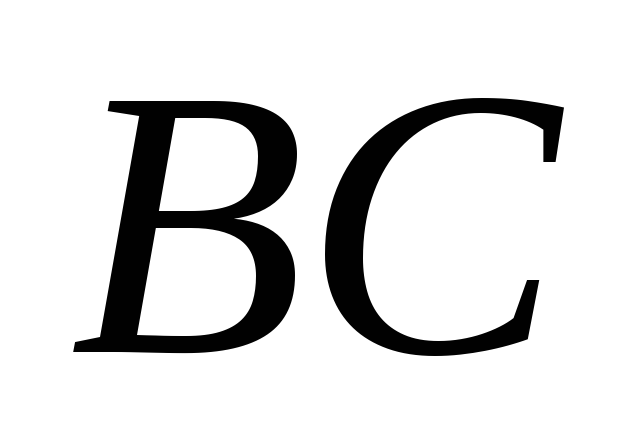 на четыре равных отрезка, а точки
на четыре равных отрезка, а точки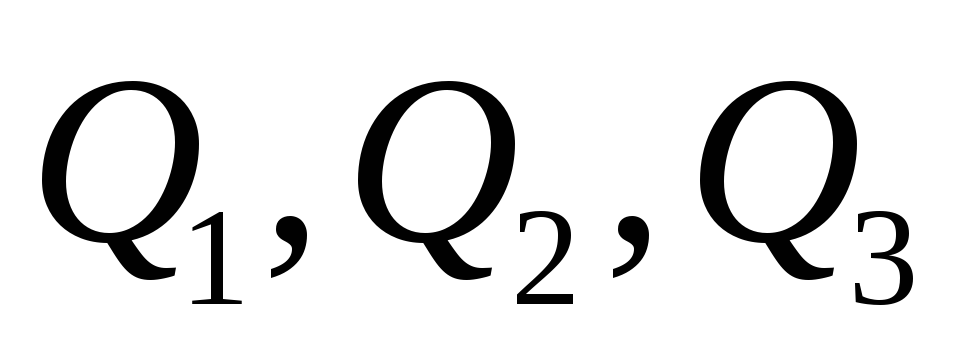 делят на четыре равные части отрезок
делят на четыре равные части отрезок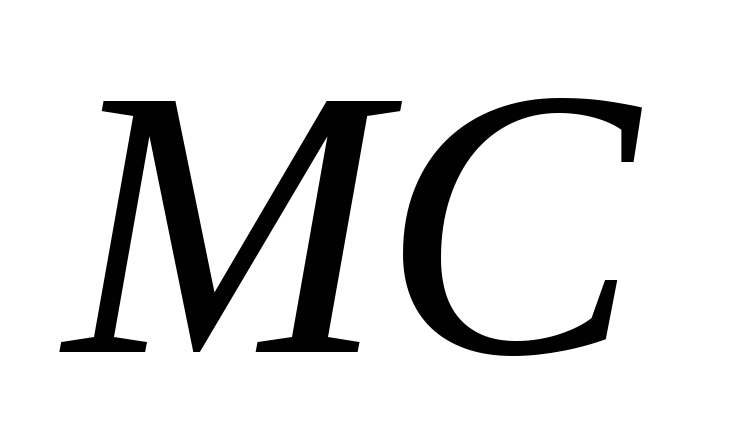 .
Считая боковое ребро равным
.
Считая боковое ребро равным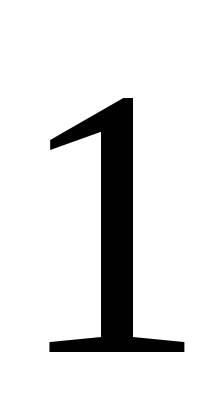 ,
найти площади треугольников
,
найти площади треугольников .
.
Домашнее задание ИДЗ. Работа №2 Составление задач на метод координат. Работа №3 Координатный метод решения задач. [9].
