
- •§2. Уравнение плоскости
- •§3. Условие параллельности плоскости и вектора
- •§4. Взаимное расположение двух плоскостей
- •§5. Геометрический смысл знака четырехчлена плоскости
- •§6. Расстояние от точки до плоскости
- •Лекция 2. Прямая в пространстве §7. Уравнение прямой в пространстве
- •§8. Взаимное расположение прямых. Расстояние между прямыми в пространстве
- •Лекция 3 - 4. Поверхности второго порядка в пространстве §9. Поверхности второго порядка. Метод сечений
- •§10. Цилиндрические поверхности
- •§11. Конические поверхности второго порядка. Конические сечения
- •§12. Поверхности вращения
- •§13. Сжатие пространства к плоскости
- •§14. Эллипсоид
- •§15. Гиперболоиды
- •§16. Параболоиды
- •§17. Прямолинейные образующие поверхностей второго порядка
- •Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
- •§1. Отображение и преобразование множеств
- •§2. Группа преобразований плоскости
- •Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
- •§4. Формулы движений
- •§5. Примеры движений
- •Лекция 3. Классификация движений плоскости §6. Теорема Шаля
- •Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
- •§8. Свойства подобий
- •Лекция 5. Аффинные преобразования плоскости, их геометрические свойства §9. Аффинные преобразования, их свойства
- •§10. Перспективно-аффинные преобразования
- •§11. Группа аффинных преобразований, её подгруппы. Эрлангенская программа ф. Клейна
- •Лекция 6. Движения пространства, их классификация §12. Движения пространства
- •Литература
§4. Формулы движений
Пусть
![]() – движение плоскости. Задав на плоскости
прямоугольную систему координат
– движение плоскости. Задав на плоскости
прямоугольную систему координат![]() ,
сможем найтиформулы
движения
,
сможем найтиформулы
движения
![]() :
это формулы, выражающие координаты
:
это формулы, выражающие координаты
![]() точки
точки![]() через координаты
через координаты![]() точки
точки![]() – прообраза точки
– прообраза точки![]() .
.
Пусть
при движении
![]() ортонормированный репер
ортонормированный репер![]() переходит в ортонормированный репер
переходит в ортонормированный репер![]() .
Тогда по теореме 2 о задании движения
парой ортонормированных реперов
следуент, что
.
Тогда по теореме 2 о задании движения
парой ортонормированных реперов
следуент, что![]() имеет координаты
имеет координаты![]() в репере
в репере![]() .
.
Рассматривая
![]() и
и![]() как старую и новую системы координат,
получаем, что точка
как старую и новую системы координат,
получаем, что точка![]() имеет соответственно старые координаты
имеет соответственно старые координаты![]() относительно репера
относительно репера![]() и новые координаты
и новые координаты![]() относительно репера
относительно репера![]() .
Используя формулы преобразования
координат при переходе от одной системы
координат к другой, получим
.
Используя формулы преобразования
координат при переходе от одной системы
координат к другой, получим
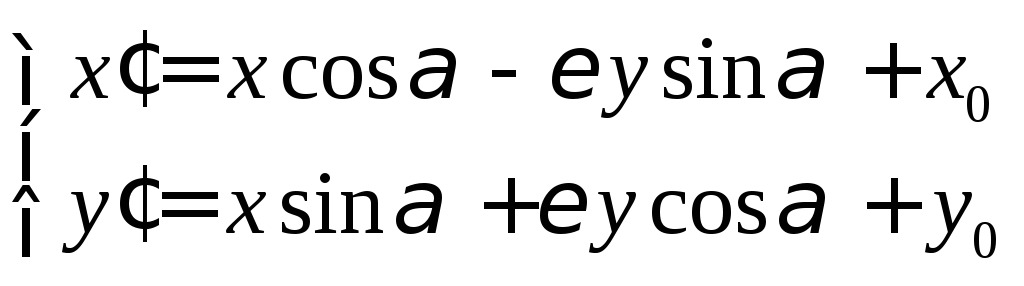 (*),
(*),
где
![]() ,
если
,
если![]() и
и![]() одинаково ориентированы, то есть
одинаково ориентированы, то есть![]() – движение первого рода, и
– движение первого рода, и![]() ,
если
,
если![]() и
и![]() противоположно ориентированы, то есть
противоположно ориентированы, то есть![]() – движение второго рода.
– движение второго рода.
Формулы
(*) это и есть формулы движения. Можно
заметить, что матрица, составленная из
коэффициентов при
![]() и
и![]() в этих формулах, являетсяортогональной
(сумма
квадратов элементов одного и того же
столбца равна 1, а сумма произведений
соответствующих элементов разных
столбцов равна 0); определитель этой
матрицы равен 1 в случае движения первого
рода и равен -1 в случае движения второго
рода.
в этих формулах, являетсяортогональной
(сумма
квадратов элементов одного и того же
столбца равна 1, а сумма произведений
соответствующих элементов разных
столбцов равна 0); определитель этой
матрицы равен 1 в случае движения первого
рода и равен -1 в случае движения второго
рода.
Имеет место следующая теорема
Т е о р
е м а 3. (об аналитическом задании движения)
Пусть
![]() – ортонормированный репер. Формулы
– ортонормированный репер. Формулы
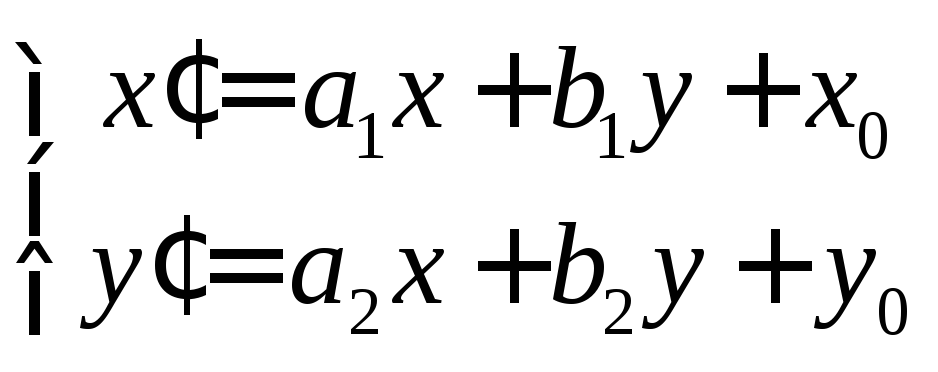 (**),
(**),
где
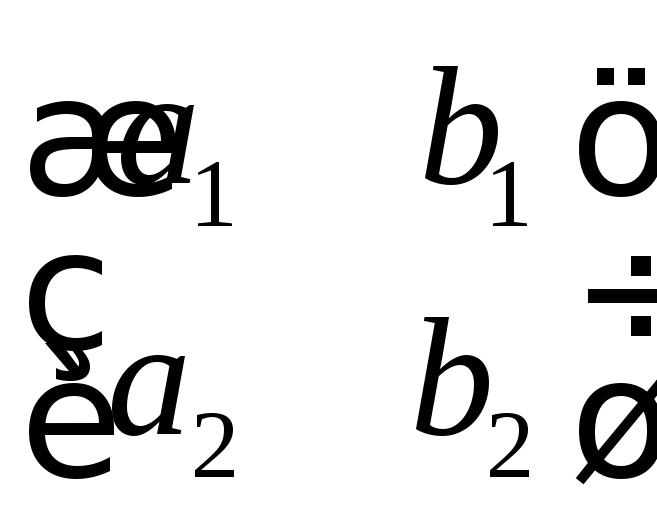 – ортогональная матрица, определяют
движение первого рода, если определитель
– ортогональная матрица, определяют
движение первого рода, если определитель![]() этой матрицы равен 1 и второго рода, если
определитель этой матрицы равен -1.
этой матрицы равен 1 и второго рода, если
определитель этой матрицы равен -1.
При доказательстве этой теоремы следует обосновать три момента:
Формулы действительно задают преобразование
 плоскости (проверить биективность).
плоскости (проверить биективность).Преобразование
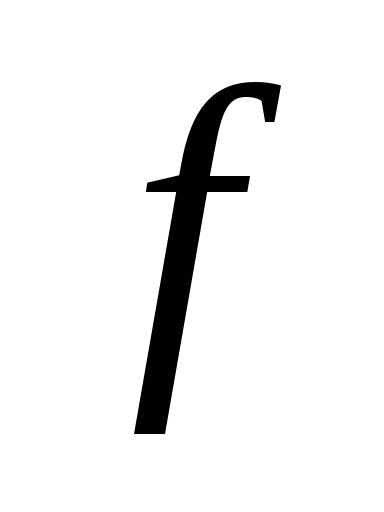 сохраняет расстояния (вычисляя расстояние
между точками
сохраняет расстояния (вычисляя расстояние
между точками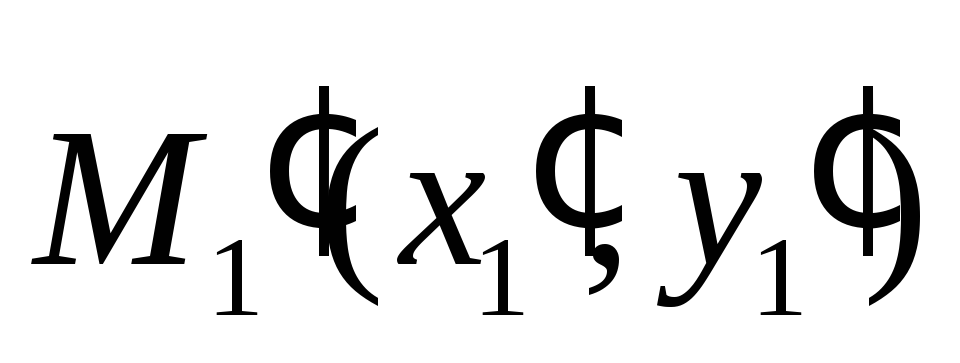 и
и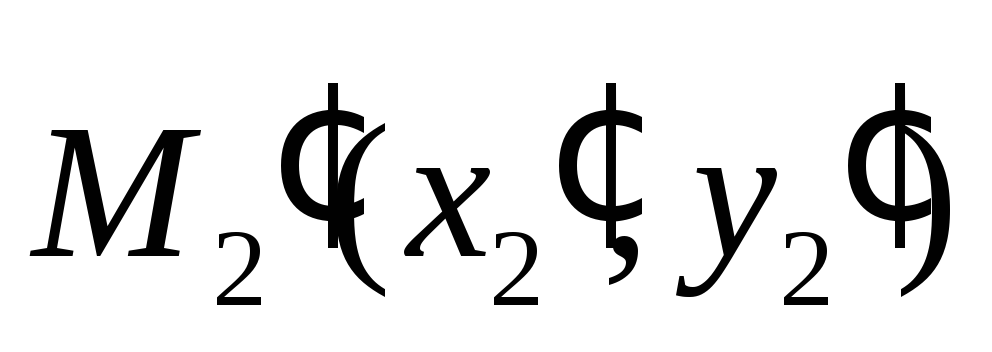 ,
использовать формулы (**) и условие
ортогональности матрицы, составленной
из коэффициентов, показать, что
,
использовать формулы (**) и условие
ортогональности матрицы, составленной
из коэффициентов, показать, что ).
).Показать, что реперы
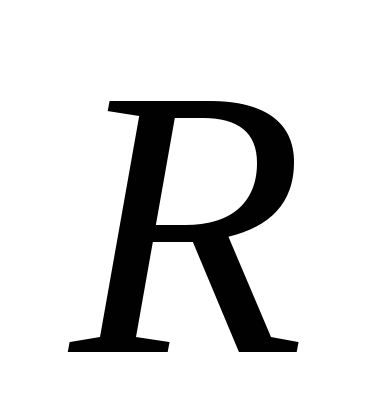 и
и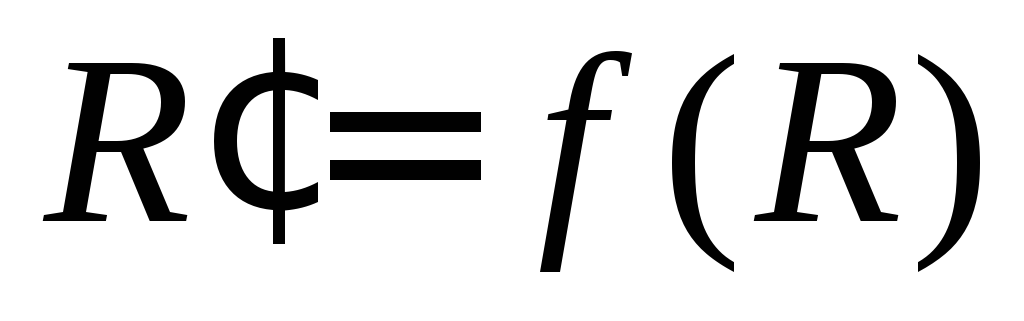 одинаково ориентированы, то есть
одинаково ориентированы, то есть является
движением первого рода, если
является
движением первого рода, если и противоположно ориентированы, то
есть
и противоположно ориентированы, то
есть – движение второго рода, если
– движение второго рода, если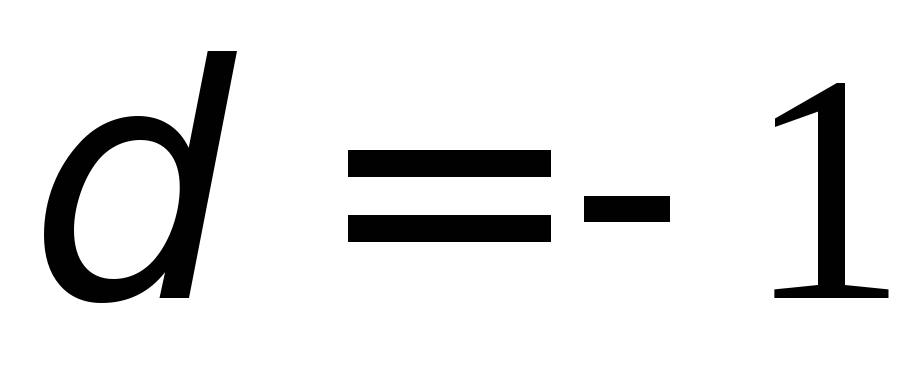 .
Для этого, используя формулы (**) нужно
найти координаты точек
.
Для этого, используя формулы (**) нужно
найти координаты точек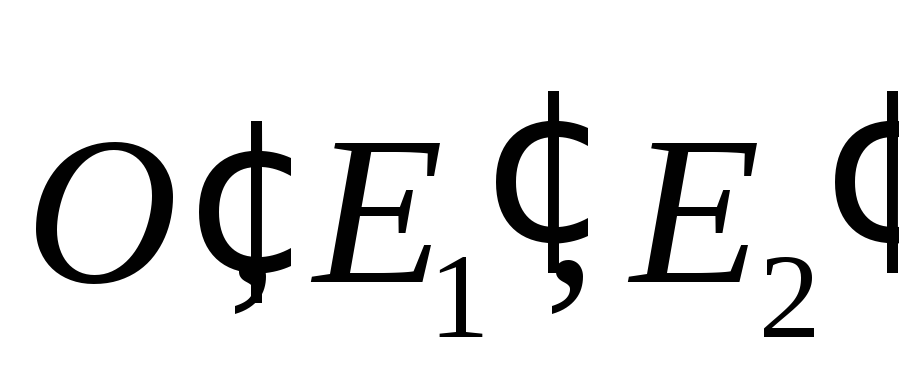 образов точек
образов точек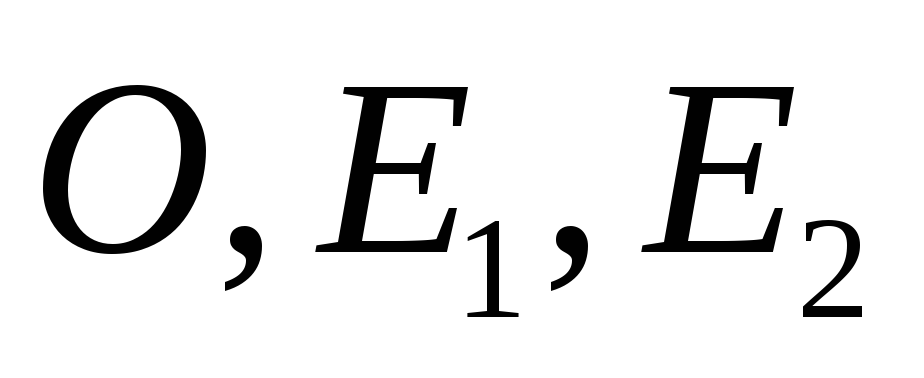 ,
определяющих репер
,
определяющих репер .
Далее найти координаты векторов
.
Далее найти координаты векторов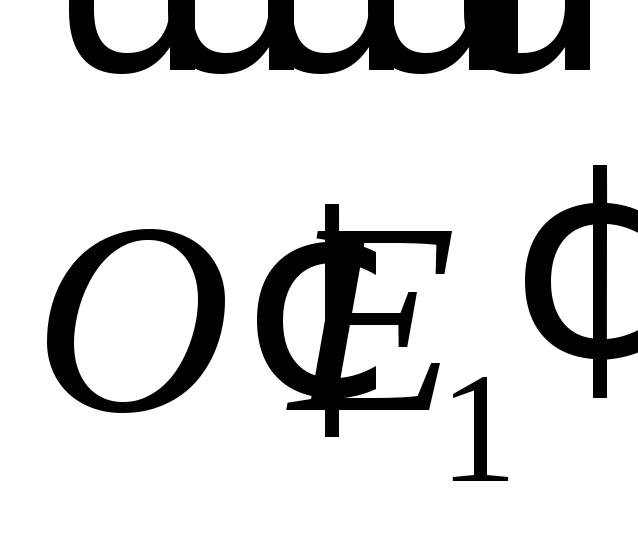 и
и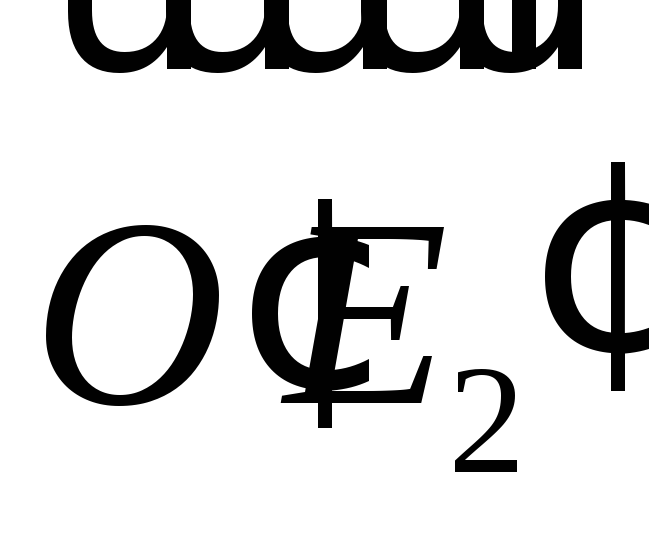 и убедиться, что матрица перехода от
базиса
и убедиться, что матрица перехода от
базиса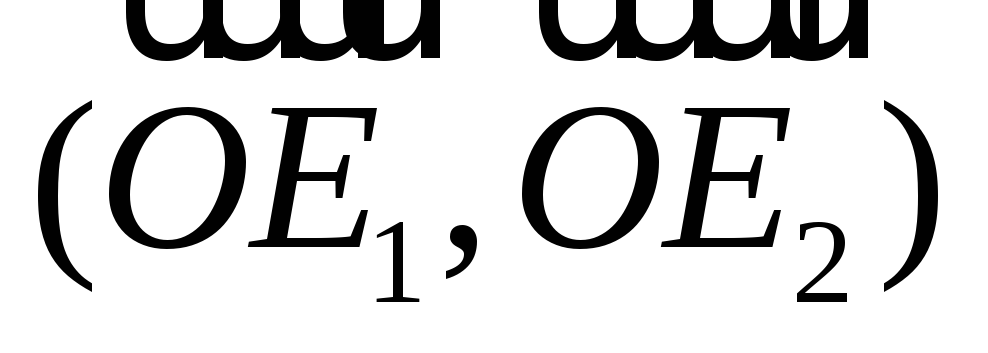 к базису
к базису имеет вид
имеет вид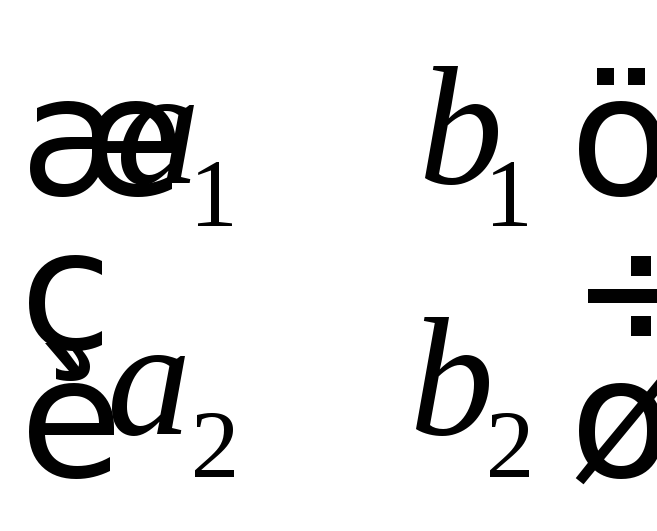 .
Знак определителя этой матрицы
характеризует одинаковость ориентации
этих базисов, а значит и реперов
.
Знак определителя этой матрицы
характеризует одинаковость ориентации
этих базисов, а значит и реперов и
и .
.
§5. Примеры движений
У п р а ж н е н и е 1. Найти формулы параллельного переноса. Доказать, что праллельный перенос является движением первого рода. Определить неподвижные точки и неподвижные прямые при параллельном переносе. Доказать, что множество всех праллельных перносов является группой.
У п р а
ж н е н и е 2. Поворотом
![]() плоскости вокруг точки
плоскости вокруг точки![]() на угол
на угол![]() называется отображение плоскости в
себя, при котором точка
называется отображение плоскости в
себя, при котором точка
![]() переходит сама в себя, любая другая
точка
переходит сама в себя, любая другая
точка![]() плоскости переходит в точку
плоскости переходит в точку![]() такую, что расстояния
такую, что расстояния![]() и
и![]() равны и угол
равны и угол![]() равен
равен![]() .
.
Задав
на плоскости прямоугольную систему
координат
![]() ,
выразите косинус и синус угла
,
выразите косинус и синус угла![]() через косинусы и синусы углов
через косинусы и синусы углов![]() и
и![]() ,
образованных векторами
,
образованных векторами![]() и
и![]() с вектором
с вектором![]() .
Далее выразите косинусы и синусы углов
.
Далее выразите косинусы и синусы углов![]() и
и![]() через координаты точек
через координаты точек![]() и
и![]() .
Убедитесь, что
.
Убедитесь, что
![]() ,
,
![]() ,
где
,
где![]() .
.
Решая
систему
![]() относительно
относительно![]() и
и![]() ,
получимформулы
поворота
,
получимформулы
поворота
![]() вокруг
начала координат:
вокруг
начала координат:
![]() .
.
Убедиться,
что поворот вокруг точки является
движением первого рода. Определить
неподвижные точки при повороте. Выяснить,
что представляет собой поворот на угол
![]() .
Доказать, что множество всех поворотов
с общим центром является группой. Найти
формулы поворота вокруг точки
.
Доказать, что множество всех поворотов
с общим центром является группой. Найти
формулы поворота вокруг точки![]() .
.
У п р а
ж н е н и е 3. Осевой
симметрией
![]() с осью
с осью
![]() называется отображение плоскости в
себя, при котором каждой точке плоскости
ставится в соответствие точка, симметричная
ей относительно прямой
называется отображение плоскости в
себя, при котором каждой точке плоскости
ставится в соответствие точка, симметричная
ей относительно прямой![]() .
.
Напомним,
что каждая точка прямой
![]() симметрична сама себе. Точка, не лежащая
на прямой
симметрична сама себе. Точка, не лежащая
на прямой![]() ,
и симметричная ей точка определяют
отрезок, перпендикулярный прмой
,
и симметричная ей точка определяют
отрезок, перпендикулярный прмой![]() ,
середина которого лежит на прямой
,
середина которого лежит на прямой![]() .
.
Найдите
формулы симметрии относительно оси
![]() ,
убедитесь, что осевая симметрия является
примером движения второго рода. Найдите
неподвижные точки, неподвижные прямые
при осевой симметрии. Выясните, что
представляет собой композиция двух
осевых симметрий с параллельными осями,
с пересекающимися осями.
,
убедитесь, что осевая симметрия является
примером движения второго рода. Найдите
неподвижные точки, неподвижные прямые
при осевой симметрии. Выясните, что
представляет собой композиция двух
осевых симметрий с параллельными осями,
с пересекающимися осями.
У п р а
ж н е н и е 4. Скользящей
симметрией
называется композиция осевой симметрии
и параллельного переноса на вектор,
параллельный оси симметрии:
![]() .
.
Показать, что скользящая симметрия является движением второго рода, отличным от осевой симметрии.
Определить неподвижные точки и неподвижные прямые при скользящей симметрии.
