
- •§2. Уравнение плоскости
- •§3. Условие параллельности плоскости и вектора
- •§4. Взаимное расположение двух плоскостей
- •§5. Геометрический смысл знака четырехчлена плоскости
- •§6. Расстояние от точки до плоскости
- •Лекция 2. Прямая в пространстве §7. Уравнение прямой в пространстве
- •§8. Взаимное расположение прямых. Расстояние между прямыми в пространстве
- •Лекция 3 - 4. Поверхности второго порядка в пространстве §9. Поверхности второго порядка. Метод сечений
- •§10. Цилиндрические поверхности
- •§11. Конические поверхности второго порядка. Конические сечения
- •§12. Поверхности вращения
- •§13. Сжатие пространства к плоскости
- •§14. Эллипсоид
- •§15. Гиперболоиды
- •§16. Параболоиды
- •§17. Прямолинейные образующие поверхностей второго порядка
- •Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
- •§1. Отображение и преобразование множеств
- •§2. Группа преобразований плоскости
- •Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
- •§4. Формулы движений
- •§5. Примеры движений
- •Лекция 3. Классификация движений плоскости §6. Теорема Шаля
- •Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
- •§8. Свойства подобий
- •Лекция 5. Аффинные преобразования плоскости, их геометрические свойства §9. Аффинные преобразования, их свойства
- •§10. Перспективно-аффинные преобразования
- •§11. Группа аффинных преобразований, её подгруппы. Эрлангенская программа ф. Клейна
- •Лекция 6. Движения пространства, их классификация §12. Движения пространства
- •Литература
§10. Цилиндрические поверхности
О п р е
д е л е н и е. Пусть в пространстве даны
линия
![]() и прямая
и прямая![]() .
Поверхность, образованная прямыми,
параллельными
.
Поверхность, образованная прямыми,
параллельными![]() и пересекающими
и пересекающими![]() ,
называетсяцилиндрической
поверхностью.
,
называетсяцилиндрической
поверхностью.
![]() –направляющая,
прямые – образующие
цилиндрической поверхности.
–направляющая,
прямые – образующие
цилиндрической поверхности.
Т е о р
е м а. Пусть
в пространстве задана прямоугольная
система координат
![]() и в плоскости
и в плоскости![]() в системе координат
в системе координат![]() задана линия
задана линия![]() .
Тогда уравнение
.
Тогда уравнение![]() определяет в пространстве цилиндрическую
поверхность с направляющей
определяет в пространстве цилиндрическую
поверхность с направляющей![]() и образующими, параллельными оси
и образующими, параллельными оси![]() .
.
Если
уравнение
![]() - уравнение второй степени, то цилиндрическая
поверхность с направляющей
- уравнение второй степени, то цилиндрическая
поверхность с направляющей![]() и образующими, параллельными оси
и образующими, параллельными оси![]() являетсяцилиндрической
поверхностью второго порядка.
являетсяцилиндрической
поверхностью второго порядка.
В зависимости от того, к какому сорту линий второго порядка относится направляющая, будем иметь:
![]() –эллиптический
цилиндр;
–эллиптический
цилиндр;
![]() –мнимый
эллиптический цилиндр;
–мнимый
эллиптический цилиндр;
![]() –гиперболический
цилиндр;
–гиперболический
цилиндр;
![]() –пара
мнимых пересекающихся плоскостей;
–пара
мнимых пересекающихся плоскостей;
![]() –пара
пересекающихся плоскостей;
–пара
пересекающихся плоскостей;
![]() –параболический
цилиндр;
–параболический
цилиндр;
![]() –пара
параллельных плоскостей;
–пара
параллельных плоскостей;
![]() –пара
мнимых пересекающихся плоскостей;
–пара
мнимых пересекающихся плоскостей;
![]() –пара
совпавших плоскостей.
–пара
совпавших плоскостей.
§11. Конические поверхности второго порядка. Конические сечения
О п р е д е л е н и е. Поверхность, образованная прямыми, проходящими через данную точку и пересекающими данную линию или имеющими относительно этой линии асимптотическое направление, называется конической поверхностью.
Если в качестве направляющей конической поверхности выбрать пару пересекающихся, пару совпавших или пару параллельных прямых и вершину, не принадлежащую плоскости этих прямых, то коническая поверхность будет представлять собой пару пересекающихся, совпавших или параллельных плоскостей (вырожденные конусы).
Пусть
в пространстве задана прямоугольная
система координат
![]() .
В плоскости, параллельной
.
В плоскости, параллельной![]() задан эллипс
задан эллипс
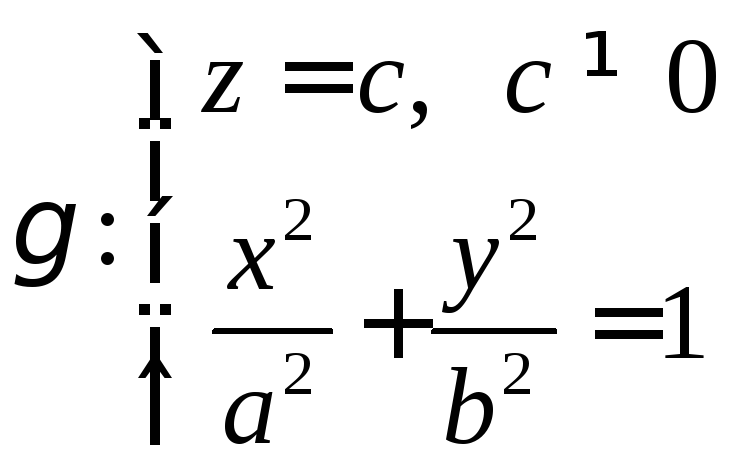 .
.
У п р а
ж н е н и е. Покажите, что уравнение
конической поверхности с вершиной
![]() и направляющей
и направляющей![]() будет иметь вид
будет иметь вид![]() – уравнениеневырожденного
конуса.
– уравнениеневырожденного
конуса.
Рассматривая сечения невырожденного конуса различными плоскостями, не проходящими через его вершину, можно получить
эллипс, если плоскость пересекает все образующие конуса;
гиперболу, если плоскость параллельна двум образующим конуса;
параболу, если плоскость параллельна только одной образующей конуса.
Эллипс, гипербола, парабола называются коническими сечениями.
Отметим, что любое однородное уравнение второй степени определяет в пространстве коническую поверхность.
§12. Поверхности вращения
О п р е
д е л е н и е. Пусть в пространстве даны
линия
![]() и прямая
и прямая![]() ,
лежащие в одной плоскости и не имеющие
общих точек. Поверхность, образованная
вращением линии
,
лежащие в одной плоскости и не имеющие
общих точек. Поверхность, образованная
вращением линии![]() вокруг прямой
вокруг прямой![]() ,
называетсяповерхностью
вращения.
,
называетсяповерхностью
вращения.
Прямая
![]() называетсяосью
вращения.
называетсяосью
вращения.
Сечения
поверхности вращения плоскостями,
проходящими через ось вращения,
представляют собой линии, равные
![]() ,
и называютсямеридианами.
,
и называютсямеридианами.
Сечения поверхности вращения плоскостями, перпендикулярными оси вращения, представляют собой окружности и называются параллелями.
Очевидно, что ось вращения является осью симметрии, а любая плоскость, проходящая через ось вращения, – плоскостью симметрии поверхности вращения.
Т
е о р е м а. В
прямоугольной системе координат
![]() в плоскости
в плоскости![]() в репере
в репере![]() задана линия
задана линия![]() .
Тогда
.
Тогда![]() – уравнение поверхности, полученной
вращением
– уравнение поверхности, полученной
вращением![]() вокруг
вокруг![]() .
.
