
- •§2. Уравнение плоскости
- •§3. Условие параллельности плоскости и вектора
- •§4. Взаимное расположение двух плоскостей
- •§5. Геометрический смысл знака четырехчлена плоскости
- •§6. Расстояние от точки до плоскости
- •Лекция 2. Прямая в пространстве §7. Уравнение прямой в пространстве
- •§8. Взаимное расположение прямых. Расстояние между прямыми в пространстве
- •Лекция 3 - 4. Поверхности второго порядка в пространстве §9. Поверхности второго порядка. Метод сечений
- •§10. Цилиндрические поверхности
- •§11. Конические поверхности второго порядка. Конические сечения
- •§12. Поверхности вращения
- •§13. Сжатие пространства к плоскости
- •§14. Эллипсоид
- •§15. Гиперболоиды
- •§16. Параболоиды
- •§17. Прямолинейные образующие поверхностей второго порядка
- •Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
- •§1. Отображение и преобразование множеств
- •§2. Группа преобразований плоскости
- •Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
- •§4. Формулы движений
- •§5. Примеры движений
- •Лекция 3. Классификация движений плоскости §6. Теорема Шаля
- •Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
- •§8. Свойства подобий
- •Лекция 5. Аффинные преобразования плоскости, их геометрические свойства §9. Аффинные преобразования, их свойства
- •§10. Перспективно-аффинные преобразования
- •§11. Группа аффинных преобразований, её подгруппы. Эрлангенская программа ф. Клейна
- •Лекция 6. Движения пространства, их классификация §12. Движения пространства
- •Литература
Министерство образования и науки РФ
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
«Уральский государственный педагогический университет»
Толстопятов В.П.
ГЕОМЕТРИЯ
Курс лекций 2 семестр
Учебное пособие
Екатеринбург
2012
Геометрия. Курс лекций / Учебное пособие / Урал. гос. пед. ун-т. – Екатеринбург, 2012. – 47 с.
Толстопятов В.П., к.ф.-м.н., профессор кафедры геометрии УрГПУ
.
Уральский государственный
педагогический университет, 2012
СОДЕРЖАНИЕ
Раздел III. Аналитическая стереометрия 4
Раздел IV. Геометрические преобразования плоскости и пространства 21
Литература 40
Раздел III. Аналитическая стереометрия
Лекция 1. Плоскость в пространстве как поверхность первого порядка. Задание полупространства. Расстояние от точки до плоскости
§1. Аффинная система координат в пространстве
О
п р е д е л е н и е. Аффинной
системой координат в пространстве
(аффинным
репером)
называется точка и три некомпланарных
вектора:
![]() .
.
Прямые
![]() ,
,![]() ,
,![]() ,
определяемые точкой
,
определяемые точкой![]() и векторами
и векторами![]() ,
,![]() ,
,![]() называются соответственно осью абсцисс,
осью ординат и осью аппликат.
называются соответственно осью абсцисс,
осью ординат и осью аппликат.
Частным
случаем аффинной системы координат
является прямоугольная
система координат
![]() ,
определяемая точкой
,
определяемая точкой![]() и ортогональными ортами
и ортогональными ортами![]() .
.
О
п р е д е л е н и е. Вектор
![]() называетсярадиус-вектором
точки
называетсярадиус-вектором
точки
![]() .
.
О п р е д е л е н и е. Координатами точки называются координаты её радиус-вектора:
![]() .
.
У п р а ж н е н и е. Построить точку по координатам в заданном аффинном репере в пространстве.
Аналогично тому, как это делалось на плоскости, с помощью координат решаются простейшие задачи
Определение координат вектора по координатам начала и конца в аффинной системе координат.
Определение координат точки по заданному простому отношению трех точек прямой и координатам двух из них в аффинной системе координат.
Вычисление расстояния между точками по координатам относительно прямоугольной системы координат
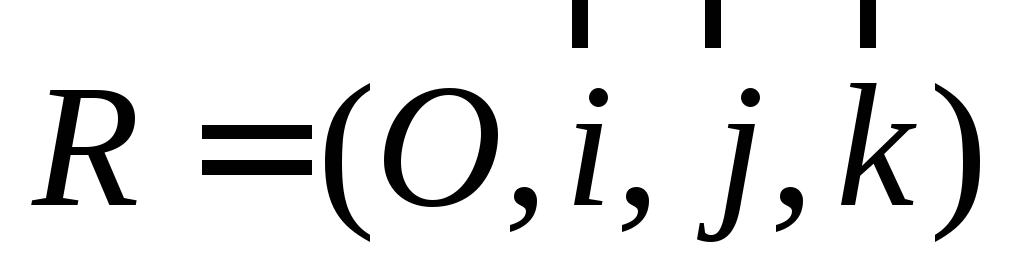 .
.
Задавая в пространстве аффинную систему координат, мы устанавливаем взаимно однозначное соответствие между точками и упорядоченными тройками действительных чисел. Это позволяет находить условие, определяющее геометрическую фигуру.
Под условием, определяющим геометрическую фигуру, понимаем упорядоченные тройки действительных чисел, уравнения, неравенства или их системы, которым удовлетворяют координаты любой точки, принадлежащей фигуре, и не удовлетворяют координаты точек, не принадлежащих фигуре.
Тогда геометрическую задачу можно перевести на язык алгебры, решить методами алгебры и полученный результат интерпретировать геометрически.
§2. Уравнение плоскости
Через
данную точку
![]() проходит единственная плоскость
проходит единственная плоскость![]() ,
параллельная двум данным неколлинеарным
векторам
,
параллельная двум данным неколлинеарным
векторам![]() и
и![]() .
.
Пусть
в пространстве задан аффинный репер
![]() и
и![]() ,
,![]() .
Точка
.
Точка![]() принадлежит плоскости
принадлежит плоскости![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы![]() компланарны, то есть вектор
компланарны, то есть вектор![]() можно выразить через векторы
можно выразить через векторы![]() и
и![]() :
:
![]() .
.
Переходя
к координатам, найдем уравнения, которым
должны удовлетворять координаты
![]() точки, принадлежащей плоскости:
точки, принадлежащей плоскости:
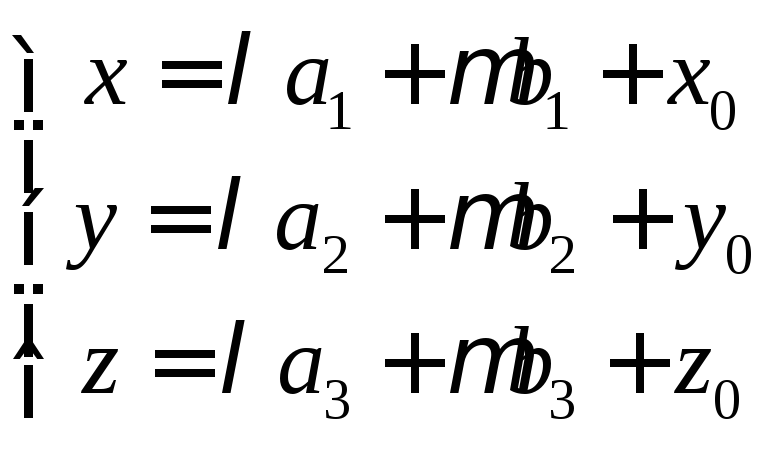 –параметрические
уравнения плоскости.
–параметрические
уравнения плоскости.
Условием
компланарности векторов
![]() является равенство нулю определителя,
составленного из координат этих векторов:
является равенство нулю определителя,
составленного из координат этих векторов:
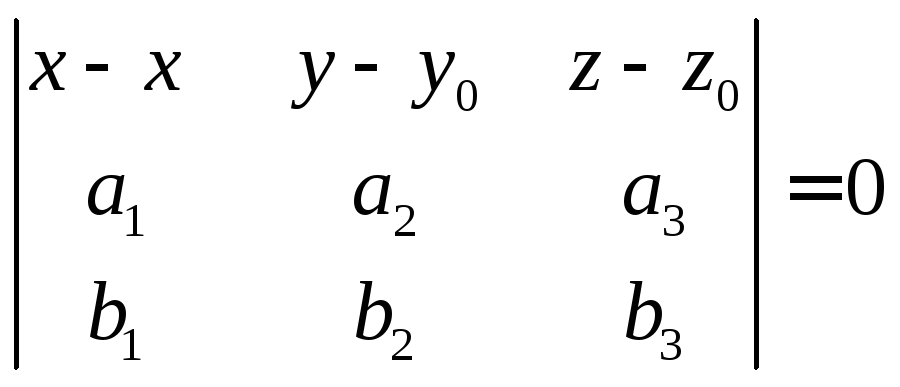 –общее
уравнение плоскости.
–общее
уравнение плоскости.
Общее уравнение плоскости приводится к виду
![]() ,
где
,
где
![]() .
.
Пусть
плоскость
![]() пересекает все три оси координат в
точках
пересекает все три оси координат в
точках![]() .
Имеем два неколлинеарных вектора
.
Имеем два неколлинеарных вектора![]() и
и![]() ,
параллельных плоскости
,
параллельных плоскости![]() .
Тогда получаем уравнение плоскости
.
Тогда получаем уравнение плоскости
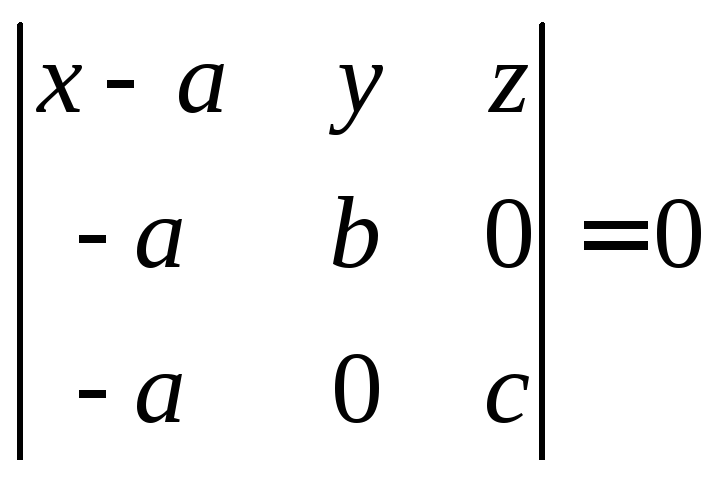 или
или
![]() –уравнение
плоскости в отрезках.
–уравнение
плоскости в отрезках.
Через
данную точку
![]() проходит единственная плоскость
проходит единственная плоскость![]() ,
перпендикулярная данному ненулевому
вектору
,
перпендикулярная данному ненулевому
вектору![]() .
Вектор
.
Вектор![]() ,
как и любой другой ненулевой вектор,
перпендикулярный плоскости
,
как и любой другой ненулевой вектор,
перпендикулярный плоскости![]() ,
называетсянормальным
вектором плоскости.
,
называетсянормальным
вектором плоскости.
Точка
![]() принадлежит плоскости
принадлежит плоскости![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы![]() и
и![]() ортогональны, то есть их скалярное
произведение равно нулю. Чтобы выразить
условие ортогональности векторов через
координаты, необходим ортонормированный
базис, а значит, в пространстве должна
быть задана прямоугольная система
координат
ортогональны, то есть их скалярное
произведение равно нулю. Чтобы выразить
условие ортогональности векторов через
координаты, необходим ортонормированный
базис, а значит, в пространстве должна
быть задана прямоугольная система
координат![]() .
Пусть
.
Пусть![]() ,
,![]() .
Выразив условие ортогональности векторов
.
Выразив условие ортогональности векторов![]() и
и![]() через координаты, получим уравнение
плоскости
через координаты, получим уравнение
плоскости![]() :
:![]() .
.
Выводы:
Чтобы составить уравнение плоскости, надо знать точку и два неколлинеарных вектора, параллельных этой плоскости, либо точку и нормальный вектор.
Уравнение плоскости приводится к виду
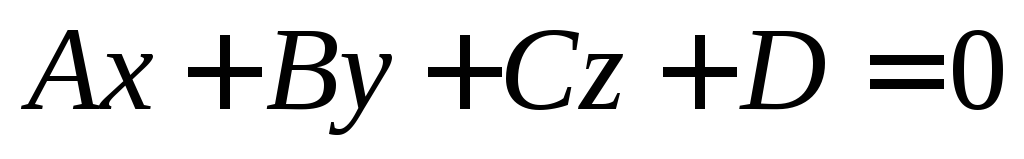 ,
где
,
где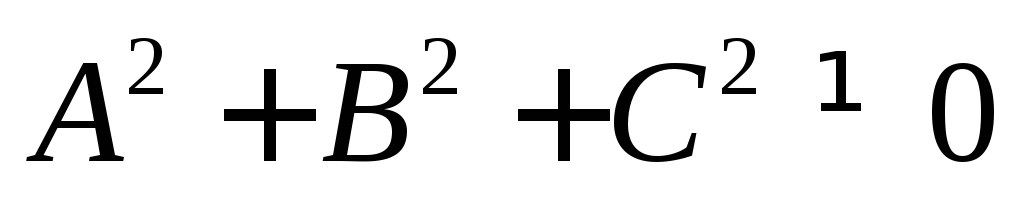 –общее
уравнение плоскости,
то есть плоскость является алгебраической
поверхностью первого порядка.
–общее
уравнение плоскости,
то есть плоскость является алгебраической
поверхностью первого порядка.
Т е о р е м а. Любая алгебраическая поверхность первого порядка является плоскостью.
Д
о к а з а т е л ь с т в о. Для алгебраической
поверхности первого порядка существует
аффинная система координат, относительно
которой поверхность задается уравнением
![]() ,
где
,
где![]() .
.
Пусть
![]() .
Приведя уравнение поверхности к виду
.
Приведя уравнение поверхности к виду![]() ,
получим равносильное уравнение
,
получим равносильное уравнение
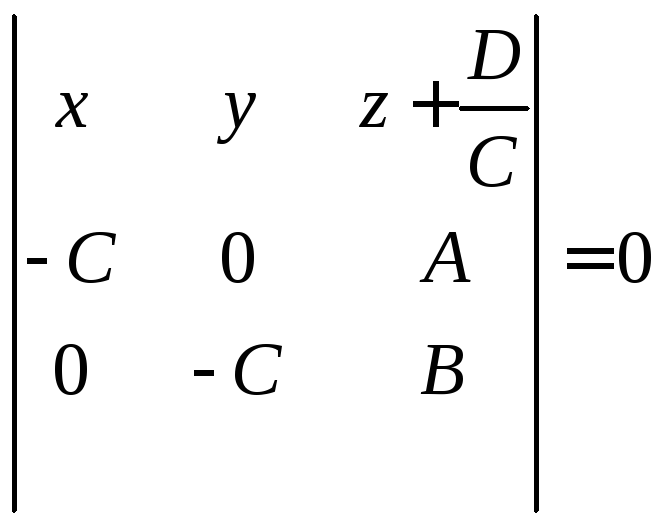 .
.
Это есть
уравнение плоскости, проходящей через
точку
![]() параллельно векторам
параллельно векторам![]() и
и![]() .
.
§3. Условие параллельности плоскости и вектора
Относительно
аффинной системы координат
![]() плоскость
плоскость![]() задана уравнением
задана уравнением![]() .
Найдем условие параллельности вектора
.
Найдем условие параллельности вектора![]() плоскости
плоскости![]() .
.
От
точки
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости![]() ,
отложим вектор
,
отложим вектор![]() .
Точка
.
Точка![]() будет иметь координаты
будет иметь координаты
![]() .
.
Вектор
![]() параллелен плоскости
параллелен плоскости![]() тогда и только тогда, когда точка
тогда и только тогда, когда точка![]() лежит в плоскости
лежит в плоскости![]() ,
то есть
,
то есть
![]() .
.
Подставляя
координаты точки
![]() и учитывая, что
и учитывая, что![]() ,
получим
условие параллельности вектора и
плоскости:
,
получим
условие параллельности вектора и
плоскости:
![]() .
(*)
.
(*)
Очевидно,
вектор
![]() не параллелен плоскости
не параллелен плоскости![]() .
Если система координат прямоугольная,
то из условия (*) следует, что вектор
.
Если система координат прямоугольная,
то из условия (*) следует, что вектор![]() ортогонален любому вектору
ортогонален любому вектору![]() ,
параллельному плоскости, то есть является
нормальным вектором этой плоскости.
,
параллельному плоскости, то есть является
нормальным вектором этой плоскости.
§4. Взаимное расположение двух плоскостей
Относительно
аффинной системы координат в пространстве
![]() две плоскости заданы своими уравнениями:
две плоскости заданы своими уравнениями:
![]() .
.
Пусть
в уравнении
![]()
![]() .
Тогда определяются точка
.
Тогда определяются точка![]() ,
принадлежащая плоскости, и два вектора
,
принадлежащая плоскости, и два вектора![]() и
и![]() ,
параллельные этой плоскости.
,
параллельные этой плоскости.
Плоскости
![]() и
и![]() совпадают тогда и только тогда, когда
векторы
совпадают тогда и только тогда, когда
векторы![]() и
и![]() параллельны плоскости
параллельны плоскости![]() и точка
и точка![]() принадлежит этой плоскости:
принадлежит этой плоскости:
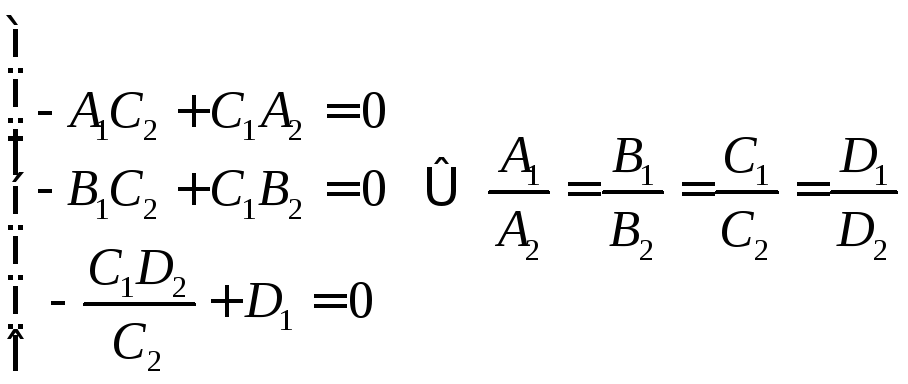 –коэффициенты
и свободные члены в общих уравнениях
плоскостей пропорциональны.
–коэффициенты
и свободные члены в общих уравнениях
плоскостей пропорциональны.
Плоскости
![]() и
и![]() параллельны тогда и только тогда, когда
векторы
параллельны тогда и только тогда, когда
векторы![]() и
и![]() параллельны плоскости
параллельны плоскости![]() и точка
и точка![]() не принадлежит этой плоскости:
не принадлежит этой плоскости:
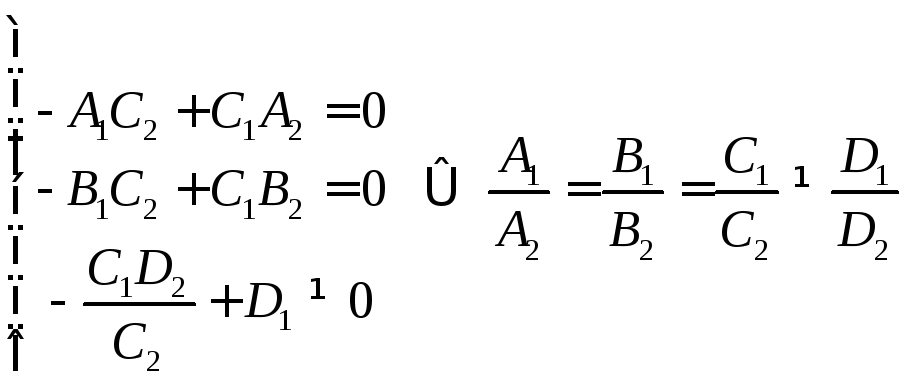 –в
общих уравнениях плоскостей коэффициенты
пропорциональны и не пропорциональны
свободным членам.
–в
общих уравнениях плоскостей коэффициенты
пропорциональны и не пропорциональны
свободным членам.
Плоскости
![]() и
и![]() пересекаются тогда и только тогда, когда
хотя бы один из векторов
пересекаются тогда и только тогда, когда
хотя бы один из векторов![]() и
и![]() не параллелен плоскости
не параллелен плоскости![]() ,
то есть имеет место хотя бы одно из
неравенств
,
то есть имеет место хотя бы одно из
неравенств![]() или
или![]() ,
а значит, в общих уравнениях плоскостей
коэффициенты не пропорциональны.
,
а значит, в общих уравнениях плоскостей
коэффициенты не пропорциональны.
