
ТЕКСТОВЫЕ ЗАДАЧИ
.docC 2 № 48. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отдалился, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Решение.
Пусть
искомое расстояние
равно ![]() км.
Скорость лодки при движении
против течения равна 4 км/ч, при
движении по течению равна 8
км/ч. Время, за которое лодка
доплывёт от места отправления
до места назначения и обратно,
равно
км.
Скорость лодки при движении
против течения равна 4 км/ч, при
движении по течению равна 8
км/ч. Время, за которое лодка
доплывёт от места отправления
до места назначения и обратно,
равно ![]() часа.
Из условия задачи следует,
что это время равно 3 часа. Составим
уравнение:
часа.
Из условия задачи следует,
что это время равно 3 часа. Составим
уравнение: ![]() .
Решив уравнение, получим
.
Решив уравнение, получим ![]() =
8 .
=
8 .
Ответ: 8 км.
C 2 № 126. Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку.
Решение.
Пусть
скорость пешехода, шедшего
из пункта A,
равна ![]() км/ч.
Тогда скорость пешехода,
шедшего из пункта B,
равна
км/ч.
Тогда скорость пешехода,
шедшего из пункта B,
равна ![]() км/ч.
Время движения пешехода
из пункта A до
места встречи
км/ч.
Время движения пешехода
из пункта A до
места встречи ![]() ч
на полчаса меньше, чем время
движения другого пешехода
ч
на полчаса меньше, чем время
движения другого пешехода
![]() ч.
Составим уравнение:
ч.
Составим уравнение: ![]() .
После преобразования оно
примет вид:
.
После преобразования оно
примет вид: ![]() Корни уравнения 6 и −3. Значит,
скорость пешехода, шедшего
из А, равна 6 км/ч.
Корни уравнения 6 и −3. Значит,
скорость пешехода, шедшего
из А, равна 6 км/ч.
Ответ: 6.
C 2 № 311564. Расстояние между пристанями А и В равно 80 км. Из А в В по течению реки отправился плот, а через 2 часа вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 22 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Решение.
Обозначим
искомую скорость (в км/ч) за ![]() .
Плот прошёл 22 км, значит, он плыл 11
часов, а яхта 9 часов. Таким образом,
имеем:
.
Плот прошёл 22 км, значит, он плыл 11
часов, а яхта 9 часов. Таким образом,
имеем:
![]() ,
,
откуда
находим ![]() .
.
Ответ: 18 км/ч.
C 2 № 311570. Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 34 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Решение.
Обозначим
искомую скорость (в км/ч) за ![]() .
Плот прошёл 34 км, значит, он плыл 17
часов, а яхта 16 часов. Таким образом,
имеем:
.
Плот прошёл 34 км, значит, он плыл 17
часов, а яхта 16 часов. Таким образом,
имеем:
![]() ,
,
откуда
находим ![]() .
.
Ответ: 16 км/ч.
C 2 № 311598. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение.
Пусть
первый оператор может выполнить
данную работу за ![]() часов,
а второй за
часов,
а второй за ![]() часов.
За один час первый оператор
выполняет
часов.
За один час первый оператор
выполняет ![]() часть
всей работы, а второй
часть
всей работы, а второй ![]() .
Составим систему уравнений:
.
Составим систему уравнений:
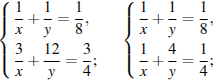
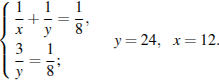
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.
C 2 № 311616. На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
Решение.
Предположим,
что ученик делает ![]() деталей
в час. Тогда мастер делает
деталей
в час. Тогда мастер делает ![]() детали
в час.
На изготовление
231 детали ученик потратит
детали
в час.
На изготовление
231 детали ученик потратит ![]() ч,
а мастер тратит
ч,
а мастер тратит ![]() ч
на изготовление 462
деталей.
Составим уравнение
по условию задачи:
ч
на изготовление 462
деталей.
Составим уравнение
по условию задачи:
![]() .
.
Решим уравнение:
![]() .
.
Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.
Ответ: 3.
C 2 № 311617. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Решение.
Пусть
за минуту в бак накачивается ![]() литров
воды. Тогда за минуту
выкачивается
литров
воды. Тогда за минуту
выкачивается ![]() л
воды.
По условию задачи
составим уравнение:
л
воды.
По условию задачи
составим уравнение:
![]() ,
,
откуда

Получаем квадратное уравнение
![]() ,
,
имеющее
корни: ![]() и
и ![]() .
.
Отбрасывая отрицательный корень, находим, что за минуту в бак накачивается 9 л воды.
Ответ: 9.
C 2 № 311653. Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Решение.
Пусть ![]() кг
и
кг
и ![]() кг
— массы первого и второго
растворов, взятые при смешивании.
Тогда
кг
— массы первого и второго
растворов, взятые при смешивании.
Тогда ![]() кг
— масса полученного раствора,
содержащего
кг
— масса полученного раствора,
содержащего ![]() кг
кислоты. Концентрация
кислоты в полученном
растворе 20 %, откуда
кг
кислоты. Концентрация
кислоты в полученном
растворе 20 %, откуда
![]()
Решим систему двух полученных уравнений:
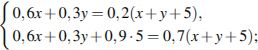

Замечание. Решение
можно сделать несколько проще,
если заметить, что из полученных
уравнений следует: ![]() ,
откуда
,
откуда ![]() .
Первое уравнение принимает
вид
.
Первое уравнение принимает
вид ![]() ,
откуда
,
откуда ![]() .
.
Ответ: 2 кг.
C 2 № 314442. Имеется два сплава с разным содержанием меди: в первом содержится 70%, а во втором — 40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50% меди?
Решение.
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,7x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,4y кг меди. Соединив два этих сплава получим сплав меди массой x + y, по условию задачи он должен содержать 0,5(x + y) меди. Следовательно, можно составить уравнение:
![]()
Выразим x через y:
![]()
Следовательно, отношение, в котором нужно взять сплавы:
![]()
Ответ: ![]()
C 2 № 311656. Найдите
целое число, если из двух следующих
утверждений верно только одно:
1) ![]() ;
2)
;
2) ![]() .
.
Решение.
Если
верно утверждение 1, то верно и
утверждение 2, а это противоречит
тому, что из этих двух утверждений
верно только одно. Следовательно,
верно только утверждение 2.
Тогда ![]() .
Этому неравенству удовлетворяет
только одно целое число:
.
Этому неравенству удовлетворяет
только одно целое число: ![]() .
.
Ответ: −17.
C 2 № 314508. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
Решение.
Заметим,
что победителем на выборах
окажется Зайцев. Пусть
количество голосов,
отданных за Зайцева равно ![]() .
Тогда за Журавлёва и Иванова
вместе отдали
.
Тогда за Журавлёва и Иванова
вместе отдали ![]() .
Процент голосов, отданных
за Борисова
.
Процент голосов, отданных
за Борисова ![]()
Ответ: 75%.
C 2 № 316268. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По
условию первая труба за одну
минуту наполняет ![]() часть
бассейна, а две трубы вместе за
одну минуту наполняют
часть
бассейна, а две трубы вместе за
одну минуту наполняют ![]() часть
бассейна. Таким образом, одна
вторая труба за минуту
наполняет
часть
бассейна. Таким образом, одна
вторая труба за минуту
наполняет ![]() часть
бассейна, то есть она наполняет
весь бассейн за 15 часов.
часть
бассейна, то есть она наполняет
весь бассейн за 15 часов.
Ответ: 15.
