
- •Задания для размышления и контроля
- •Лекция №1. Теоремы в школьном курсе математики
- •Прием аналитико-синтетического поиска доказательства
- •Приемы поиска косвенного доказательства
- •1) Доказательство «от противного» (частный случай нисходящего анализа)
- •7 Класс
- •Задание для самостоятельной работы
- •Литература
Практическое занятие №1 Организация учебно-познавательной деятельности учащихся при работе с теоремой
Цели
1. Сформировать представление у студентов о методике изучения теорем школьного курса математики.
2. Тренировать способность у студентов к применению полученных знаний в будущей профессиональной деятельности.
В результате изучения темы студент должен знать:
определение понятия «теорема»;
основные части теоремы;
виды теорем;
методические подходы к процессу организации работы с теоремой.
Студент должен уметь:
осуществлять логико-математический анализ теорем;
применять полученные знания в будущей профессиональной деятельности.
Литература
Груденов, Я.И. Изучение определений, аксиом и теорем / Я.И. Груденов. – М., 1981. – 95 с.
Далингер, В.А. Методика работы над формулировкой доказательством и закреплением теоремы / В.А. Далингер. – Омск, 1995. – 198 с.
Далингер, В.А. Обучение учащихся доказательству теорем / В.А. Далингер. – Омск, 2002. – 420 с.
Далингер, В.А. Теорема, её виды и методы доказательства. / В.А. Далингер. – Омск, 1996. – 76 с.
Дразнин, И.Е. О применении обратных и противоположных теорем в курсе геометрии / И.Е. Дразнин // Математика в школе, 1994. – №6.
Новосельцева, З.И. Некоторые примеры мотивации изучения теорем / З.И. Новосельцева // Математика в школе, 1985. – №5.
Петриченко, Щ. достаточно или необходимо / Щ. Петриченко // Математика: приложение к 1 сентября. – №23.
Саранцев, Г.И. Обучение математическим доказательствам в школе / Г.И. Саранцев. – М., 2000. – 173 с.
Тимофеева, И.Л. Некоторые замечания о методе доказательства от противного / И.Л. Тимофеев // Математика в школе, 1994. – №3.
Шумихина, В.В. Использование «разрезных» теорем на уроках геометрии / В.В. Шумихина // Математика в школе, 1994. – №3.
Задания для размышления и контроля
Охарактеризуйте понятия «теорема», «аксиома» через понятие «доказательство»
Перечислите возможные варианты логической структуры формулировки теорем, приведите примеры теорем школьного курса математики разных структур.
Выделите основные элементы теорем, рассмотрите формулировки с различными структурами.
Охарактеризуйте основные виды доказательств теорем.
Перечислите достоинства и недостатки аналитического и синтетического методов доказательства теорем.
Укажите различия методов доказательства восходящего анализа и нисходящего анализа.
Выполните логико-математический анализ одной из теорем.
Разработайте систему заданий на применение данной теоремы.
Предложите и обоснуйте методику изучения выбранной теоремы, через описание:
способа знакомства учащихся с фактом, описанном в теореме;
способа введения формулировки теоремы;
способа краткой записи (а при необходимости и чертежа) для усвоения ее содержания;
способа ознакомления с доказательством теоремы;
способа записи доказательства.
Лекция №1. Теоремы в школьном курсе математики
План
Теоремы и доказательства (сведения из логики).
Методические основы обучения доказательствам.
Математическое предложение, истинность которого устанавливается посредством доказательства, называют теоремой.
Структура доказательства
тезис – суждение, истинность которого доказывается.
аргументы доказательства – суждения, истинность которых установлена и из которых необходимо следует истинность доказываемого тезиса (определения понятий, аксиомы, постулаты, теоремы, общие законы науки).
демонстрация – логический процесс взаимосвязи суждений, при котором осуществляется переход от аргументов к тезису.
Виды формулировок теорем
категорическая
пример 1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
пример 2. Постоянный множитель можно выносить за знак производной
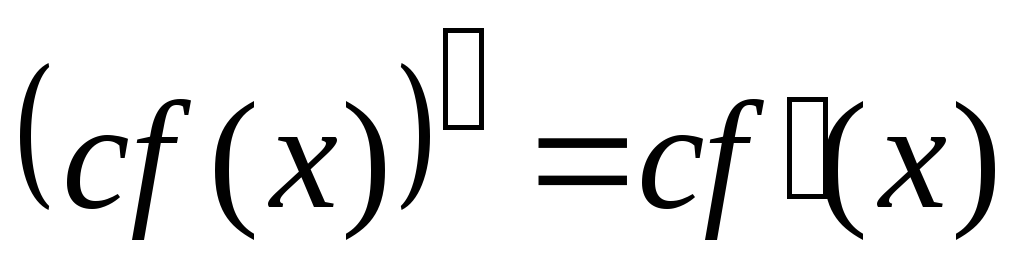 .
.
условная (импликативная)
пример 1. Если в треугольнике два угла равны, то треугольник равнобедренный.
пример 2. Если
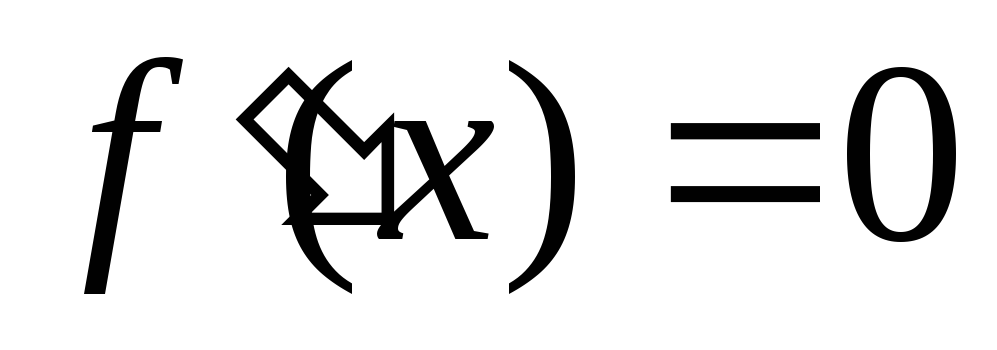 на некотором промежутке, то на этом
промежутке
на некотором промежутке, то на этом
промежутке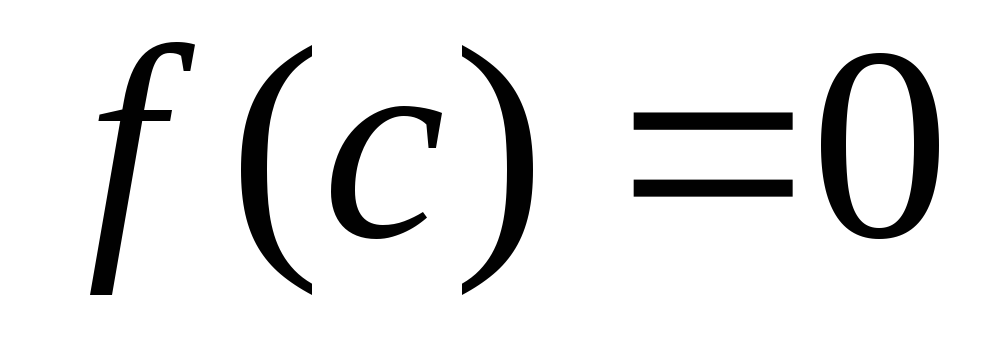 ,
где с
– постоянная.
,
где с
– постоянная.
раздельная
пример 1. Плоскость и не лежащая на ней прямая либо не пересекаются, либо пересекаются в одной точке.
пример 2. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
Структура формулировки теоремы
условие;
заключение;
разъяснительная часть.
Логическая структура условия и заключения:
конъюнктивная;
дизъюнктивная.
Виды теорем
P
 Q
– прямое
утверждение (теорема);
Q
– прямое
утверждение (теорема);Q
 P
– обратное
утверждение (теорема);
P
– обратное
утверждение (теорема);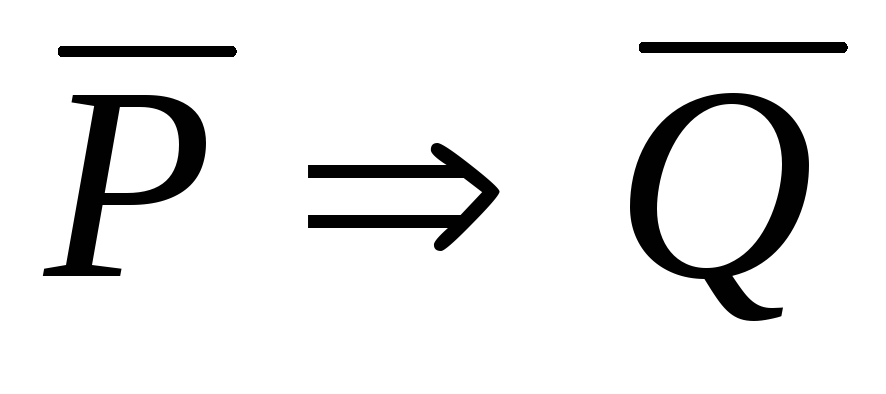 –противоположное
утверждение (теорема);
–противоположное
утверждение (теорема); –контрапозитивное
утверждение (теорема).
–контрапозитивное
утверждение (теорема).
P![]() Q
и
Q
и
![]() ;
Q
;
Q
![]() P
и
P
и
![]() –
пары равносильных утверждений (теорем).
–
пары равносильных утверждений (теорем).
Пример.
Прямая теорема: «Если два угла треугольника равны, то и стороны, лежащие против этих углов, равны».
Обратная теорема: «Если две стороны треугольника равны, то и углы, лежащие против этих сторон, равны».
Противоположная теорема: «Если два угла треугольника не равны, то и стороны, лежащие против этих углов, не равны».
Контрапозитивная теорема: «Если две стороны треугольника не равны, то и углы, лежащие против этих сторон, не равны».
Методы доказательства теорем
Метод доказательства – способ связи аргументов при переходе от условия к заключению.
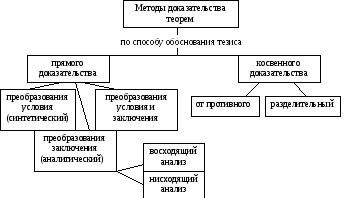
Рис. 4
Логико-математический анализ теоремы
Логико-математический анализ – раскрытие логической структуры предложения, вида суждения и способа его конструирования. Он предполагает:
установление формы формулировки;
определение вида суждения;
перевод формулировки, если необходимо, в импликативную форму;
запись структуры теоремы, т.е. вычленение разъяснительной части, условия, заключения с выделением простых высказываний и логических связок;
формулирование обратного утверждения и определение его истинности.
Математический анализ – раскрытие математического содержания выделенных элементов структуры.
Этапы изучения теоремы учащимися (по Г.И. Саранцеву)
мотивация изучения;
ознакомление с фактом, отраженным в теореме;
формулировка теоремы;
усвоение содержания теоремы, ее структуры;
ознакомление со способом доказательства;
доказательство теоремы;
применение теоремы;
установление связи с другими теоремами.
Методы введения теоремы
конкретно- индуктивный метод;
абстрактно – дедуктивный метод.
Обучение учащихся доказательству
Обучение доказательству – обучение мыслительным процессам поиска, нахождения и построения доказательства, а не воспроизведению и заучиванию готовых доказательств.
Приемы поиска прямого доказательства
