
- •§2. -Мерное аффинное пространство
- •§3. Аффинная система координат
- •§4. -Мерные плоскости
- •§5. Уравнения -мерных плоскостей
- •§6. Определение некоторых фигур аффинного пространства
- •Лекция 2.-мерное евклидово (точечное) пространство §7. Евклидово векторное пространство
- •§8. Евклидово -мерное точечное пространство
- •Раздел VI. Проективная геометрия Лекция 1.Проективное n-мерное пространство. Модели проективной прямой и плоскости
- •§1. Центральное проектирование. Предмет проективной геометрии
- •§2. Аксиоматическое определение проективного пространства. Модели проективной прямой и проективной плоскости
- •Лекция 2. Проективные реперы на прямой и плоскости. Уравнение прямой на проективной плоскости §3. Проективные координаты
- •§4. Однородные аффинные координаты
- •§5. Уравнение прямой на проективной плоскости
- •Лекция 3. Принцип двойственности. Теорема Дезарга §6. Принцип двойственности. Теорема Дезарга
- •Лекция 4. Сложные отношения точек и прямых. Гармонические четверки точек и прямых в полном четырехвершиннике §7. Сложное отношение четырех точек прямой
- •§8. Сложное отношение четырех прямых пучка
- •§9. Гармонические четверки
- •Лекция 5. Проективные отображения. Проективные преобразования. Предмет проективной геометрии §10. Проективные преобразования плоскости
- •§11. Проективные отображения прямых и пучков
- •Лекция 6. Квадрики на проективной плоскости. Полюсы и поляры §12. Линии второго порядка на проективной плоскости
- •§13. Полюсы и поляры. Поляритет
- •§14. Классификация линий второго порядка на проективной плоскости
- •§15. Овальные линии второго порядка
- •Лекция 7. Аффинная и евклидова геометрии с проективной точки зрения §16. Проективная модель аффинной плоскости
- •§17. Проективная модель евклидовой плоскости
- •Раздел VII. Топология Лекция 1. Топологическое пространство. Индуцированная топология. Топологические подпространства §1. Метрические пространства
- •§2. Определение и примеры топологических пространств
- •§3. Индуцированная топология. Топологическое подпространство
- •§4. Замкнутые множества
- •§5. Окрестности. Типы точек. Замыкание
- •Лекция 2. Непрерывные отображения и гомеоморфизмы. Предмет топологии. Связность и компактность как основные инварианты топологического пространства §6. Непрерывность и гомеоморфизм
- •§7. Примеры топологических инвариантов
- •Лекция 3. Замкнутые поверхности в трехмерном пространстве и их классификация §8. Понятие поверхности. Замкнутые поверхности
- •§9. Ориентируемость поверхности. Эйлерова характеристика
- •§10. Топологические свойства проективной плоскости
- •Литература
§5. Уравнение прямой на проективной плоскости
Пусть
на проективной плоскости выбран
проективный репер
![]() .
Прямая
.
Прямая![]() задана точками
задана точками![]() и . Найдем уравнение прямой
и . Найдем уравнение прямой![]() .
.
Точка
![]() принадлежит прямой
принадлежит прямой![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы![]() принадлежат одному двумерному векторному
подпространству, а значит, образуют
линейно зависимую систему. Имеем
принадлежат одному двумерному векторному
подпространству, а значит, образуют
линейно зависимую систему. Имеем![]() ,
,![]() ,или
,или −параметрические
уравнения прямой
−параметрические
уравнения прямой
![]() .
.
С
другой стороны, система векторов
![]() является линейно зависимой тогда и
только тогда, когда определитель,
составленный из координат этих векторов,
равен нулю
является линейно зависимой тогда и
только тогда, когда определитель,
составленный из координат этих векторов,
равен нулю
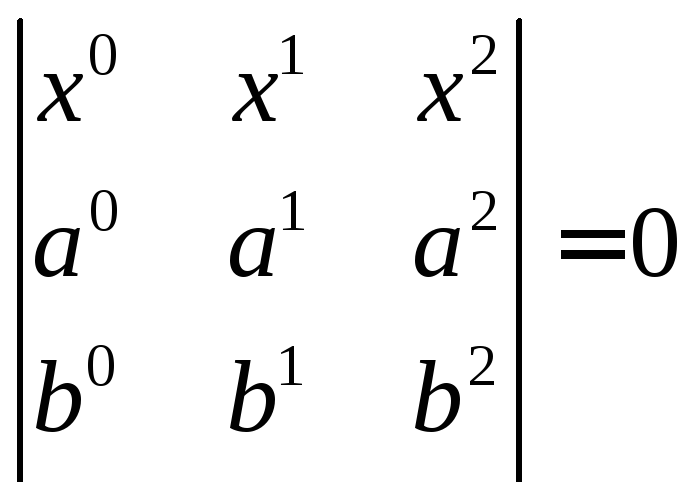 .
.
Получаем линейное однородное уравнение
![]() −общее
уравнение прямой
−общее
уравнение прямой
![]() .
.
Т е о р е м а. Всякое линейное однородное уравнение определяет проективную прямую.
Тройка коэффициентов в уравнении проективной прямой определяется с точностью до общего множителя, отличного от нуля, и называется координатами проективной прямой.
Лекция 3. Принцип двойственности. Теорема Дезарга §6. Принцип двойственности. Теорема Дезарга
Пусть
на проективной плоскости P
задан репер
![]() .
Каждой точке
.
Каждой точке![]() плоскости можно поставить в соответствие
прямую
плоскости можно поставить в соответствие
прямую![]() с такими же координатами. Каждой прямой
с такими же координатами. Каждой прямой![]() с координатами
с координатами![]() можно поставить в соответствие точку
можно поставить в соответствие точку![]() с такими же координатами. Таким образом,
будем иметь биективное отображение
с такими же координатами. Таким образом,
будем иметь биективное отображение![]() множества всех точек и прямых плоскости
в себя. При этом, если
множества всех точек и прямых плоскости
в себя. При этом, если![]() ,
то есть
,
то есть![]() ,
то прямая
,
то прямая![]() проходит через точку
проходит через точку![]() .
Это значит, что отображение
.
Это значит, что отображение![]() сохраняет отношение принадлежности
точек и прямых. Отсюда следует принцип
двойственности на проективной плоскости:
сохраняет отношение принадлежности
точек и прямых. Отсюда следует принцип
двойственности на проективной плоскости:
Если
на проективной плоскости справедливо
предложение
![]() относительно
точек, прямых и их взаимной принадлежности,
то справедливо и двойственное утверждение
относительно
точек, прямых и их взаимной принадлежности,
то справедливо и двойственное утверждение![]() ,
которое
получается из
,
которое
получается из
![]() заменой
слова «точка» словом «прямая», слова
«прямая» − словом «точка», слов «лежит
на» − словами «проходит через», слов
«проходит через» − словами «лежит на».
заменой
слова «точка» словом «прямая», слова
«прямая» − словом «точка», слов «лежит
на» − словами «проходит через», слов
«проходит через» − словами «лежит на».
Примеры двойственных предложений
 :
Через любые две точки проективной
плоскости проходит единственная
проективная прямая.
:
Через любые две точки проективной
плоскости проходит единственная
проективная прямая.
![]() :
Любые две прямые проективной плоскости
пересекаются в одной точке.
:
Любые две прямые проективной плоскости
пересекаются в одной точке.
 :
На проективной прямой существуют, по
крайней мере, три различные точки.
:
На проективной прямой существуют, по
крайней мере, три различные точки.
![]() :
Через каждую точку проходят, по крайней
мере, три различные прямые.
:
Через каждую точку проходят, по крайней
мере, три различные прямые.
 :
На проективной плоскости существуют
три точки, не лежащие на одной прямой.
:
На проективной плоскости существуют
три точки, не лежащие на одной прямой.
![]() :
На проективной плоскости существуют
три прямые, не проходящие через одну
точку.
:
На проективной плоскости существуют
три прямые, не проходящие через одну
точку.
У п р а ж н е н и е. Определить фигуры, двойственные
а) прямой (множеству всех точек, лежащих на одной прямой);
б) пучку прямых;
в) отрезку прямой;
г) трехвершиннику – фигуре, состоящей из трех точек, не лежащих на одной прямой, и трех прямых, попарно соединяющих эти точки.
Пусть
в проективном пространстве заданы два
трехвершинника
![]() и . Вершины
и . Вершины![]() и
и![]() ,
,![]() и
и![]() ,
и
,
и![]() назовем соответственными вершинами, а
прямые и
назовем соответственными вершинами, а
прямые и![]() ,
и
,
и![]() ,
,![]() и
и![]() − соответственными сторонами
трехвершинников.
− соответственными сторонами
трехвершинников.
Если прямые, соединяющие соответственные вершины трехвершинников, пересекаются в одной точке, то назовем эту точку центром перспективы этих трехвершинников.
Если точки пересечения соответственных сторон лежат на одной прямой, то назовем эту прямую осью перспективы этих трехвершинников.
Т е о р е м а Дезарга. Если два трехвершинника имеют центр перспективы, то они имеют и ось перспективы.
Доказательство теоремы для трехвершинников, расположенных в расширенном пространстве можно найти в [13].
Справедлива и обратная теорема. В случае трехвершинников, расположенных в одной плоскости, обратная теорема совпадает с утверждением, двойственным теореме Дезарга, и, следовательно, она справедлива по принципу двойственности.
В связи с теоремой Дезарга на плоскости можно рассмотреть фигуру, образованную десятью точками и десятью прямыми – конфигурация Дезарга. Каждой из десяти прямых принадлежат три точки, и через каждую из точек проходят три прямые. Все точки и прямые этой конфигурации равноправны, каждая из них может играть любую роль в отношении теоремы Дезарга.
Теорема Дезарга дает возможность решения ряда задач элементарной геометрии на доказательство и на построение одной линейкой. Примеры таких задач можно найти в пособии [13].
