
- •§2. -Мерное аффинное пространство
- •§3. Аффинная система координат
- •§4. -Мерные плоскости
- •§5. Уравнения -мерных плоскостей
- •§6. Определение некоторых фигур аффинного пространства
- •Лекция 2.-мерное евклидово (точечное) пространство §7. Евклидово векторное пространство
- •§8. Евклидово -мерное точечное пространство
- •Раздел VI. Проективная геометрия Лекция 1.Проективное n-мерное пространство. Модели проективной прямой и плоскости
- •§1. Центральное проектирование. Предмет проективной геометрии
- •§2. Аксиоматическое определение проективного пространства. Модели проективной прямой и проективной плоскости
- •Лекция 2. Проективные реперы на прямой и плоскости. Уравнение прямой на проективной плоскости §3. Проективные координаты
- •§4. Однородные аффинные координаты
- •§5. Уравнение прямой на проективной плоскости
- •Лекция 3. Принцип двойственности. Теорема Дезарга §6. Принцип двойственности. Теорема Дезарга
- •Лекция 4. Сложные отношения точек и прямых. Гармонические четверки точек и прямых в полном четырехвершиннике §7. Сложное отношение четырех точек прямой
- •§8. Сложное отношение четырех прямых пучка
- •§9. Гармонические четверки
- •Лекция 5. Проективные отображения. Проективные преобразования. Предмет проективной геометрии §10. Проективные преобразования плоскости
- •§11. Проективные отображения прямых и пучков
- •Лекция 6. Квадрики на проективной плоскости. Полюсы и поляры §12. Линии второго порядка на проективной плоскости
- •§13. Полюсы и поляры. Поляритет
- •§14. Классификация линий второго порядка на проективной плоскости
- •§15. Овальные линии второго порядка
- •Лекция 7. Аффинная и евклидова геометрии с проективной точки зрения §16. Проективная модель аффинной плоскости
- •§17. Проективная модель евклидовой плоскости
- •Раздел VII. Топология Лекция 1. Топологическое пространство. Индуцированная топология. Топологические подпространства §1. Метрические пространства
- •§2. Определение и примеры топологических пространств
- •§3. Индуцированная топология. Топологическое подпространство
- •§4. Замкнутые множества
- •§5. Окрестности. Типы точек. Замыкание
- •Лекция 2. Непрерывные отображения и гомеоморфизмы. Предмет топологии. Связность и компактность как основные инварианты топологического пространства §6. Непрерывность и гомеоморфизм
- •§7. Примеры топологических инвариантов
- •Лекция 3. Замкнутые поверхности в трехмерном пространстве и их классификация §8. Понятие поверхности. Замкнутые поверхности
- •§9. Ориентируемость поверхности. Эйлерова характеристика
- •§10. Топологические свойства проективной плоскости
- •Литература
Министерство образования и науки РФ
Федеральное государственное бюджетное
образовательное учреждение
высшего профессионального образования
«Уральский государственный педагогический университет»
Толстопятов В.П.
ГЕОМЕТРИЯ
Курс лекций 3 семестр
Учебное пособие
Екатеринбург
2012
Геометрия. Курс лекций 3 семестр / Учебное пособие / Урал. гос. пед. ун-т. – Екатеринбург, 2012. – 77 с.
Толстопятов В.П., к.ф.-м.н., профессор кафедры геометрии УрГПУ
.
Уральский государственный
педагогический университет, 2012
СОДЕРЖАНИЕ
Раздел V. Многомерные пространства 4
Раздел VI. Проективная геометрия 13
Раздел VII. Топология 48
Литература 62
Раздел V. Многомерные пространства
Лекция 1.![]() -мерное
аффинное (точечное) пространство.
-мерное
аффинное (точечное) пространство.![]() -плоскости
и их взаимное расположение
-плоскости
и их взаимное расположение
§1. Воспоминания о будущем
В математике новые идеи рождаются и развиваются, прежде всего, под влиянием требований, предъявляемых к ней другими науками, техникой.
Другим двигателем развития математики является её внутренняя логика, например, обобщение уже известных идей.
Вспомним,
что рассматривая геометрическое
пространство
![]() ,
мы определили свободный вектор как
множество всех сонаправленных отрезков
одинаковой длины.
,
мы определили свободный вектор как
множество всех сонаправленных отрезков
одинаковой длины.
Множество
![]() всех свободных векторов геометрического
пространства является трехмерным
векторным пространством.
всех свободных векторов геометрического
пространства является трехмерным
векторным пространством.
Для
того, чтобы задать свободный вектор,
достаточно указать его представитель
– направленный отрезок, а значит, задать
упорядоченную пару точек. Таким образом,
имеем отображение
![]() .
.
При
этом было показано, что любой вектор
можно отложить от данной точки, то есть
для любой точки
![]() и любого вектора
и любого вектора![]() существует единственная точка
существует единственная точка![]() такая, что
такая, что![]() .
.
Для
свободных векторов было определено
сложение по правилу треугольника. Таким
образом, для любых трех точек
![]() имеет место векторное равенство
имеет место векторное равенство![]() .
.
Обобщая
эти наблюдения можно дать аксиоматическое
определение
![]() -мерного
аффинного пространства.
-мерного
аффинного пространства.
§2. -Мерное аффинное пространство
Пусть
![]() –
–![]() -мерное
векторное пространство над полем
-мерное
векторное пространство над полем![]() действительных чисел. (Повторите
аксиоматическое определение
действительных чисел. (Повторите
аксиоматическое определение![]() -мерного
векторного пространства, модели векторных
пространств).
-мерного
векторного пространства, модели векторных
пространств).
О
п р е д е л е н и е. Непустое множество
![]() называетсяаффинным
называетсяаффинным
![]() -мерным
пространством,
если задано отображение
-мерным
пространством,
если задано отображение
![]() (будем обозначать
(будем обозначать![]() ),
удовлетворяющее аксиомам Вейля:
),
удовлетворяющее аксиомам Вейля:
![]() .
.
![]() .
.
Элементы
множества
![]() будем называтьточками.
будем называтьточками.
Векторное
пространство
![]() называетсяпространством
переносов аффинного пространства.
называетсяпространством
переносов аффинного пространства.
Примеры (модели) аффинных пространств:
Из предыдущего параграфа следует, что прямая, плоскость, пространство, рассматриваемые в школьном курсе геометрии, являются примерами соответственно одномерного, двумерного и трехмерного аффинного пространства.
Пусть
 –
– -мерное
векторное пространство над полем
-мерное
векторное пространство над полем действительных чисел. И пусть
действительных чисел. И пусть .
Определим отображение
.
Определим отображение по следующему правилу:
по следующему правилу: .
Несложно проверить выполнение аксиом
Вейля.
.
Несложно проверить выполнение аксиом
Вейля.
EMBED Equation.DSMT4
![]() .
.
![]()
![]()
Арифметическая модель аффинного
 -мерного
пространства.
-мерного
пространства.
Возьмем
![]() и
и![]() (точки и векторы – упорядоченные наборы
из
(точки и векторы – упорядоченные наборы
из![]() действительных чисел). Определим
отображение
действительных чисел). Определим
отображение![]() по следующему правилу:
по следующему правилу:
![]() .
.
Аналогично предыдущему примеру несложно проверить выполнение аксиом Вейля.
§3. Аффинная система координат
По
аналогии с трехмерным геометрическим
пространством определим аффинную
систему координат
в
![]() -мерном
аффинном пространстве
-мерном
аффинном пространстве![]() с пространством переносов
с пространством переносов![]() как точку и базис:
как точку и базис:![]() .
.
Координатами
точки
назовем координаты её радиус-вектора:
![]() .
.
Очевидно,
если
![]() ,
то
,
то![]() .
.
§4. -Мерные плоскости
Пусть
![]() –
–![]() -мерное
подпространство
-мерное
подпространство![]() -мерного
векторного пространства
-мерного
векторного пространства![]() .
.
Напомним,
что подмножество
![]() векторного пространства
векторного пространства![]() являетсявекторным
подпространством
тогда и только тогда, когда выполняются
следующие условия:
являетсявекторным
подпространством
тогда и только тогда, когда выполняются
следующие условия:
 ;
; .
.
Приведите примеры векторных пространств и их подпространств.
О
п р е д е л е н и е.
![]() -мерной
плоскостью с направляющим подпространством
-мерной
плоскостью с направляющим подпространством![]() ,
проходящей через точку
,
проходящей через точку![]() ,
называется множество всех точек аффинного
пространства таких, что вектор
,
называется множество всех точек аффинного
пространства таких, что вектор
![]() принадлежит пространству
принадлежит пространству![]() :
:
![]() .
.
Примеры
![]() -плоскостей:
-плоскостей:
 –нульмерное
векторное пространство.
–нульмерное
векторное пространство.
![]() –каждая
точка – нульмерная плоскость.
–каждая
точка – нульмерная плоскость.
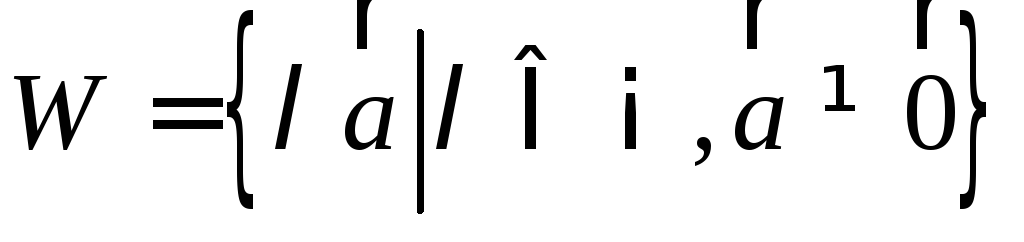 –одномерное
векторное пространство.
–одномерное
векторное пространство.
![]() –прямая.
–прямая.
Максимальная размерность подпространства
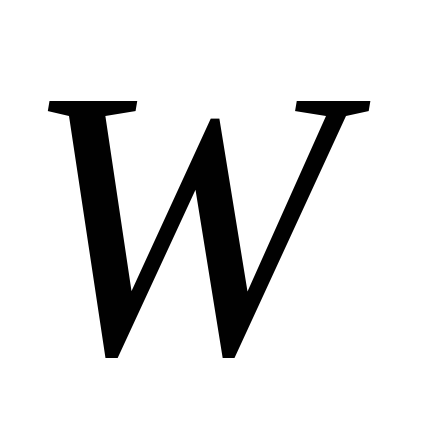
 -мерного
векторного пространства может быть
-мерного
векторного пространства может быть .
.
![]() -мерная
плоскость называется гиперплоскостью.
-мерная
плоскость называется гиперплоскостью.
Так в геометрическом пространстве, рассматриваемом в школьном курсе геометрии, плоскости играют роль гиперплоскостей, прямые – роль одномерных плоскостей.
Отметим
свойства
![]() -плоскостей
-плоскостей
Если
 ,
то
,
то .
Таким образом, если две
.
Таким образом, если две -плоскости
имеют общую точку и обющее направляющее
подпространство, то они совпадают.
-плоскости
имеют общую точку и обющее направляющее
подпространство, то они совпадают.Для любых точек

 -плоскости
-плоскости вектор
вектор принадлежит
принадлежит .
. -мерная
плоскость
-мерная
плоскость
 является
является -мерным
аффинным пространством с пространством
переносов
-мерным
аффинным пространством с пространством
переносов .
.Точки
 аффинного пространства называютсяточками
общего положения,
если векторы
аффинного пространства называютсяточками
общего положения,
если векторы
 образуют линейно независимую систему.
образуют линейно независимую систему.
Имеет место обобщение известных аксиом школьного курса геометрии о прямой и плоскости
Для
любых
![]() точек общего положения (
точек общего положения (![]() )
существует единственная
)
существует единственная![]() -мерная
плоскость, проходящая через эти точки.
-мерная
плоскость, проходящая через эти точки.
