- •Уроки 1–2 Повторение. Решение задач
- •Ход уроков
- •III. Итоги уроков.
- •Понятие вектора. Равенство векторов. (8 часов) Урок 1 Понятие вектора. Равенство векторов
- •Ход урока
- •III. Итоги урока.
- •Урок 2 Сумма двух векторов. Законы сложения векторов. Правило параллелограмма
- •Ход урока
- •I. Анализ результатов самостоятельной работы.
- •III. Выполнение практических заданий и упражнений.
- •IV. Итоги урока.
- •III. Закрепление изученного материала.
- •IV. Самостоятельная работа (обучающего характера).
- •III. Решение задач и упражнений.
- •IV. Проверочная самостоятельная работа.
- •V. Итоги урока.
- •Урок 5 Произведение вектора на число
- •Ход урока
- •II. Закрепление изученного материала.
- •II. Решение задач.
- •III. Проверочная самостоятельная работа.
- •IV. Итоги урока.
- •V. Итоги урока.
- •Урок 8 Средняя линия трапеции
- •Ход урока
- •I. Проверка усвоения учащимися материала.
- •II. Объяснение нового материала.
- •IV. Проверочная самостоятельная работа.
- •III. Изучение нового материала.
- •V. Итоги урока.
- •IV. Самостоятельная работа контролирующего характера.
- •1)Координаты середины отрезка.
- •2)Вычисление длины вектора по его координатам.
- •3) Расстояние между двумя точками.
- •IV. Итоги урока.
- •II. Решение задач.
- •III. Итоги урока.
- •Урок 5 Уравнение линии на плоскости. Уравнение окружности
- •Ход урока
- •II. Объяснение нового материала.
- •IV. Итоги урока.
- •III. Итоги урока.
- •Урок 7 Уравнение прямой
- •Ход урока
- •II. Изучение нового материала.
- •IV. Итоги урока.
- •Уроки 8–9 решение задач
- •Ход уроков
- •II. Решение задач.
- •III. Опрос учащихся по теоретическому материалу.
- •IV. Решение задач.
- •V. Итоги уроков.
- •III. Итоги урока.
- •IV. Итоги урока.
- •Урок 2 формулы приведения. Формулы для вычисления координат точки
- •Ход урока
- •II. Изучение нового материала.
- •IV. Итоги урока.
- •II. Объяснение нового материала.
- •IV. Итоги урока.
- •III. Решение задач.
- •IV. Итоги урока.
- •III. Решение задач.
- •III. Самостоятельная работа контролирующего характера.
- •IV. Итоги урока.
- •Урок 9 Угол между векторами. Скалярное произведение векторов
- •Ход урока
- •II. Объяснение нового материала.
- •Скалярное произведение векторов
- •II. Изучение нового материала.
- •Скалярное произведение в координатах
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Урок 11 Решение задач
- •Ход урока
- •II. Решение задач.
- •III. Устный опрос учащихся по карточкам.
- •IV. Итоги уроков.
- •Длина окружности. Площадь круга. (11 часов)
- •III. Изучение нового материала.
- •IV. Закрепление изученного материала.
- •II. Работа с учебником.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •III. Итоги урока.
- •Урок 5 Длина окружности
- •Ход урока
- •IV. Итоги урока.
- •Урок 6 Площадь круга
- •Ход урока
- •III. Итоги урока.
- •IV. Итоги урока.
- •IV. Итоги урока.
- •Уроки 9–10 Решение задач по материалу главы XII
- •Ход уроков
- •II. Решение задач.
- •III. Проверочная самостоятельная работа.
- •Движения. (8 часов)
- •III. Изучение нового материала.
- •IV. Закрепление изученного материала.
- •V. Итоги уроков.
- •Урок 4 Параллельный перенос
- •Ход урока
- •I. Проверка изученного материала.
- •II. Изучение нового материала.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Уроки 5–6 Поворот
- •Ход уроков
- •III. Закрепление изученного материала.
- •V. Итоги уроков.
- •Урок 8 Контрольная работа № 4
- •Ход урока
- •I. Организация учащихся на выполнение работы.
- •II. Выполнение работы по вариантам.
- •Начальные сведения из стереометрии (7 часов) Урок 1 Предмет стереометрии. Многогранник
- •Ход урока
- •I. Изучение нового материала.
- •II. Закрепление изученного материала.
- •III. Итоги урока.
- •Урок 2 Призма. Параллелепипед
- •Ход урока
- •I. Устная работа.
- •II. Объяснение нового материала.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Урок 3 Объем тела. Свойства прямоугольного параллелепипеда
- •Ход урока
- •I. Проверка домашнего задания.
- •II. Изучение нового материала.
- •III. Выполнение упражнений и решение задач.
- •IV. Итоги урока.
- •Урок 4 Пирамида
- •Ход урока
- •I. Актуализация опорных знаний учащихся.
- •II. Работа учащихся по учебнику.
- •III. Выполнение упражнений. Решение задач.
- •IV. Итоги урока. Выставление оценок.
- •Урок 5 Цилиндр
- •Ход урока
- •I. Объяснение нового материала.
- •II. Закрепление изученного материала.
- •III. Итоги урока.
- •III. Выполнение упражнений.
- •IV. Итоги урока.
- •Урок 7 Сфера и шар
- •Ход урока
- •II. Работа с учебником.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Об аксиомах и планиметрии (2 часа)
- •Решение задач
- •Треугольник
- •Окружность
- •Четырехугольники. Многоугольники
- •Векторы. Метод координат. Движения
- •Литература
1)Координаты середины отрезка.
Используя формулу из п. 84 (1)
![]() и координаты векторов
и координаты векторов![]() записать равенство в координатах:
записать равенство в координатах:![]() отсюдаx=
отсюдаx=![]() ;y=
;y=![]() .
.
Вывод:каждая координата середины отрезка равна полусумме соответствующих координат его концов.
џУстно решить задачу № 936.
2)Вычисление длины вектора по его координатам.
Используя рис. 280 учебника, вывести
формулу
![]() ,
если
,
если![]()
џУстно решить задачу № 938.
3) Расстояние между двумя точками.
Пусть точка M1(x1;y1)
и точкаM2(x2;y2);
тогда вектор![]() (x2–x1;y2–y1); следовательно, длина
этого вектора может быть найдена по
формуле
(x2–x1;y2–y1); следовательно, длина
этого вектора может быть найдена по
формуле![]() но
но![]() =d, таким образом, расстояниеd между
точкамиM1(x1;y1)
иM2(x2;y2)
выражается формулой
=d, таким образом, расстояниеd между
точкамиM1(x1;y1)
иM2(x2;y2)
выражается формулой
d=![]()
џРешить задачу № 940 (а, б) на доске и в тетрадях.
III. Закрепление изученного материала (решение задач).
1. Решить задачу № 939.
Решение
Найти расстояние от точки М (3; –2):
а) до оси абсцисс; точкаВ (x;y)
лежит на оси абсцисс; тогда расстояние
равно 2; б) расстояние до оси ординат
равно 3; в) до начала координат равноd=![]()
2. Решить задачу № 941 на доске и в тетрадях.
Решение
PΔ=MN+NP+MP;
MN=![]()
NP=![]()
MP=![]()
PΔMNP=![]() .
.
IV. Итоги урока.
Задание на дом:изучить материал пунктов 88, 89; решить задачи №№ 935, 952.
Урок 4 Простейшие задачи в координатах. Решение задач
Цели:закрепить знания учащихся в ходе решения задач; учить решать задачи в координатах.
Ход урока
I. Повторение изученного материала.
1. Двое учащихся по карточкам работают у доски:
Карточка 1
1) Вывести формулы координат середины отрезка.
2) Решить задачу № 942.
Карточка 2
1) Вывести формулу расстояния между двумя точками.
2) Решить задачу № 937.
2. С остальными учащимися проводится устная работа по решению задач:
1) Найдите координаты вектора
![]() ,
равного разности векторов
,
равного разности векторов![]() и
и![]() ,
если
,
если![]() (–5;
6),
(–5;
6),![]() (0;
–4).
(0;
–4).
2) Найдите координаты вектора
![]() ,
равного сумме векторов
,
равного сумме векторов![]() и
и![]() ,
если
,
если![]() (3;
7),
(3;
7),![]() (4;
–5).
(4;
–5).
3) Найдите координаты середины отрезка DK, еслиD (–6; 4),K (2; –8).
4) Найдите длину отрезка CP, еслиС (3; –2),P (–5; 4).
5) Найдите длину вектора
![]() ,
равного
,
равного![]() ,
если
,
если![]() (5;
0) и
(5;
0) и![]() (0;
–12).
(0;
–12).
6) Найдите координаты вектора 3![]() ,
если
,
если![]() (4;
–2); вектора –2
(4;
–2); вектора –2![]() ,
если
,
если![]() (–2;
5).
(–2;
5).
II. Решение задач.
1. Решить задачу № 947 (а).
Решение
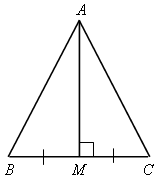
Найдем длины сторон треугольника АВСпо формуле
d=![]() :
:
AB=![]()
BC=![]()
|
AC=
Так как АВ = АС, то по
определению равнобедренного
треугольникаАВС – равнобедренный.
Найдем его площадь; проведем высотуАМ
SΔABC= |
|
Пусть М (x;y), тогда
x=![]() = 3;y=
= 3;y=![]() = –1.
= –1.
Значит, точка М (3; –1).
Найдем длину отрезка AM=![]()
Площадь треугольника АВС
равнаS=![]() = 13.
= 13.
Ответ: 13.
2. Решить задачу № 946 (б).
Решение
M1(–1;x) иM2(2x; 3);M1M2=d= 7. Найтиx.
d=![]() ; (2x+ 1)2+ (3 –x)2= 72;
; (2x+ 1)2+ (3 –x)2= 72;
4x2+ 4x+ 1 + 9 – 6x+x2= 49; 5x2– 2x– 39 = 0;
D=b2– 4ac= 4 + 780 = 784;
![]()
![]()
Ответ: –2,6; 3.
3. Решить задачу № 948 (б) на доске и в тетрадях.
Решение
Пусть точка М (0;y) лежит на оси ординат; по условиюМС = MD;
(4 – 0)2 + (–3 – y)2 = (8 – 0)2 + (1 – y)2;
16 + 9 + 6y + y2 = 64 + 1 – 2y + y2;
8y= 40;
y= 5.
Значит, точка М (0; 5).
Ответ: (0; 5).
4. Решить задачу № 950 (б) на доске и в тетрадях.
|
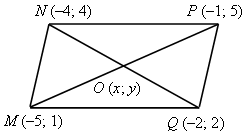
Решение Найдем координаты точки пересечения диагоналей четырехугольника О (x;y): для диагоналиNQимеем:
x= |
|
y=![]() = 3; точка О (–3; 3).
= 3; точка О (–3; 3).
Для диагонали МР имеем:
x=![]() = –3;y=
= –3;y=![]() = 3; точка О (–3; 3).
= 3; точка О (–3; 3).
Значит, диагонали MPиNQточкой пересечения делятся пополам; по признаку параллелограммаMNPQ – параллелограмм.
MP=![]()
NQ=![]()
Ответ: 4![]() и 2
и 2![]() .
.
5. Решить задачу № 951 (а).
Решение
AB=![]() =
4;
=
4;
CD=![]() =
4;
=
4;
BC=![]() =
2;
=
2;
AD=![]() =2.
=2.
Так как AB = CD =4 иBC = AD = 2, то по II
признаку параллелограммаABCD –параллелограмм. Найдем диагоналиАСиBD параллелограммаABCD:AC=![]()
BD=![]()
Если диагонали равны AC = BD, тоABCD – прямоугольник.
S=AD∙AB= 2 ∙ 4 = 8.
Ответ: 8.