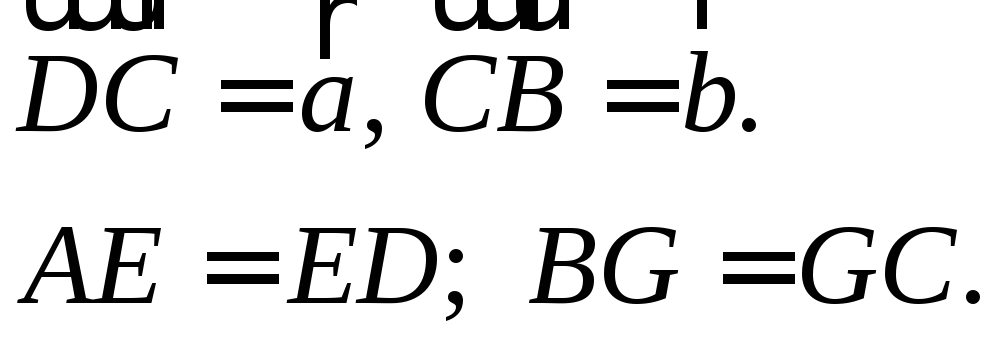- •Уроки 1–2 Повторение. Решение задач
- •Ход уроков
- •III. Итоги уроков.
- •Понятие вектора. Равенство векторов. (8 часов) Урок 1 Понятие вектора. Равенство векторов
- •Ход урока
- •III. Итоги урока.
- •Урок 2 Сумма двух векторов. Законы сложения векторов. Правило параллелограмма
- •Ход урока
- •I. Анализ результатов самостоятельной работы.
- •III. Выполнение практических заданий и упражнений.
- •IV. Итоги урока.
- •III. Закрепление изученного материала.
- •IV. Самостоятельная работа (обучающего характера).
- •III. Решение задач и упражнений.
- •IV. Проверочная самостоятельная работа.
- •V. Итоги урока.
- •Урок 5 Произведение вектора на число
- •Ход урока
- •II. Закрепление изученного материала.
- •II. Решение задач.
- •III. Проверочная самостоятельная работа.
- •IV. Итоги урока.
- •V. Итоги урока.
- •Урок 8 Средняя линия трапеции
- •Ход урока
- •I. Проверка усвоения учащимися материала.
- •II. Объяснение нового материала.
- •IV. Проверочная самостоятельная работа.
- •III. Изучение нового материала.
- •V. Итоги урока.
- •IV. Самостоятельная работа контролирующего характера.
- •1)Координаты середины отрезка.
- •2)Вычисление длины вектора по его координатам.
- •3) Расстояние между двумя точками.
- •IV. Итоги урока.
- •II. Решение задач.
- •III. Итоги урока.
- •Урок 5 Уравнение линии на плоскости. Уравнение окружности
- •Ход урока
- •II. Объяснение нового материала.
- •IV. Итоги урока.
- •III. Итоги урока.
- •Урок 7 Уравнение прямой
- •Ход урока
- •II. Изучение нового материала.
- •IV. Итоги урока.
- •Уроки 8–9 решение задач
- •Ход уроков
- •II. Решение задач.
- •III. Опрос учащихся по теоретическому материалу.
- •IV. Решение задач.
- •V. Итоги уроков.
- •III. Итоги урока.
- •IV. Итоги урока.
- •Урок 2 формулы приведения. Формулы для вычисления координат точки
- •Ход урока
- •II. Изучение нового материала.
- •IV. Итоги урока.
- •II. Объяснение нового материала.
- •IV. Итоги урока.
- •III. Решение задач.
- •IV. Итоги урока.
- •III. Решение задач.
- •III. Самостоятельная работа контролирующего характера.
- •IV. Итоги урока.
- •Урок 9 Угол между векторами. Скалярное произведение векторов
- •Ход урока
- •II. Объяснение нового материала.
- •Скалярное произведение векторов
- •II. Изучение нового материала.
- •Скалярное произведение в координатах
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Урок 11 Решение задач
- •Ход урока
- •II. Решение задач.
- •III. Устный опрос учащихся по карточкам.
- •IV. Итоги уроков.
- •Длина окружности. Площадь круга. (11 часов)
- •III. Изучение нового материала.
- •IV. Закрепление изученного материала.
- •II. Работа с учебником.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •III. Итоги урока.
- •Урок 5 Длина окружности
- •Ход урока
- •IV. Итоги урока.
- •Урок 6 Площадь круга
- •Ход урока
- •III. Итоги урока.
- •IV. Итоги урока.
- •IV. Итоги урока.
- •Уроки 9–10 Решение задач по материалу главы XII
- •Ход уроков
- •II. Решение задач.
- •III. Проверочная самостоятельная работа.
- •Движения. (8 часов)
- •III. Изучение нового материала.
- •IV. Закрепление изученного материала.
- •V. Итоги уроков.
- •Урок 4 Параллельный перенос
- •Ход урока
- •I. Проверка изученного материала.
- •II. Изучение нового материала.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Уроки 5–6 Поворот
- •Ход уроков
- •III. Закрепление изученного материала.
- •V. Итоги уроков.
- •Урок 8 Контрольная работа № 4
- •Ход урока
- •I. Организация учащихся на выполнение работы.
- •II. Выполнение работы по вариантам.
- •Начальные сведения из стереометрии (7 часов) Урок 1 Предмет стереометрии. Многогранник
- •Ход урока
- •I. Изучение нового материала.
- •II. Закрепление изученного материала.
- •III. Итоги урока.
- •Урок 2 Призма. Параллелепипед
- •Ход урока
- •I. Устная работа.
- •II. Объяснение нового материала.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Урок 3 Объем тела. Свойства прямоугольного параллелепипеда
- •Ход урока
- •I. Проверка домашнего задания.
- •II. Изучение нового материала.
- •III. Выполнение упражнений и решение задач.
- •IV. Итоги урока.
- •Урок 4 Пирамида
- •Ход урока
- •I. Актуализация опорных знаний учащихся.
- •II. Работа учащихся по учебнику.
- •III. Выполнение упражнений. Решение задач.
- •IV. Итоги урока. Выставление оценок.
- •Урок 5 Цилиндр
- •Ход урока
- •I. Объяснение нового материала.
- •II. Закрепление изученного материала.
- •III. Итоги урока.
- •III. Выполнение упражнений.
- •IV. Итоги урока.
- •Урок 7 Сфера и шар
- •Ход урока
- •II. Работа с учебником.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Об аксиомах и планиметрии (2 часа)
- •Решение задач
- •Треугольник
- •Окружность
- •Четырехугольники. Многоугольники
- •Векторы. Метод координат. Движения
- •Литература
Урок 5 Произведение вектора на число
Цели:ввести понятие умножения вектора на число; рассмотреть основные свойства умножения вектора на число.
Ход урока
I. Изучение нового материала (лекция).
1. Целесообразно в начале лекции привести пример, подводящий к определению произведения вектора на число, в частности такой:
Автомобиль движется прямолинейно со
скоростью
![]() .
Его обгоняет второй автомобиль,
двигающийся со скоростью, вдвое большей.
Навстречу им движется третий автомобиль,
у которого величина скорости такая же,
как у второго автомобиля. Как выразить
скорости второго и третьего автомобилей
через скорость
.
Его обгоняет второй автомобиль,
двигающийся со скоростью, вдвое большей.
Навстречу им движется третий автомобиль,
у которого величина скорости такая же,
как у второго автомобиля. Как выразить
скорости второго и третьего автомобилей
через скорость![]() первого автомобиля и как изобразить с
помощью векторов эти скорости?
первого автомобиля и как изобразить с
помощью векторов эти скорости?
|
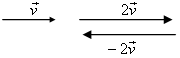
Ответ дает рисунок. Естественно
считать, что скорость второго автомобиля
равна 2 |
|
2. Определение
произведения вектора на число, его
обозначение:![]() (рис. 260).
(рис. 260).
3. Записать в тетрадях:
1) произведение любого вектора на число нуль есть нулевой вектор;
2) для любого числа k и любого вектора
![]() векторы
векторы![]() и
и![]() коллинеарны.
коллинеарны.
4. Основные свойства умножения вектора на число:
Для любых чисел k,l и любых
векторов![]() справедливы равенства:
справедливы равенства:
1°.
![]() (сочетательный закон) (рис. 261);
(сочетательный закон) (рис. 261);
2°. ![]() (первый распределительный закон) (рис.
262);
(первый распределительный закон) (рис.
262);
3°.
![]() (второй распределительный закон) (рис.
263).
(второй распределительный закон) (рис.
263).
Примечание. Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях.
Например:
![]()
![]()
II. Закрепление изученного материала.
1. Выполнить практические задания № 776 (б; г; д), 777.
2. Решить задачи № 779, 781 (а; в) на доске и в тетрадях.
Решение
Дано:![]()
а)
![]()
в)
![]()
3. Решить задачу № 780 (б).
III. Итоги урока.
Домашнее задание:изучить материал пункта 83; ответить на вопросы 14–17, с. 214; решить задачи №№ 775, 776 (а, в, е), 781 (б), 780 (а).
Урок 6 Решение задач. Произведение вектора на число
Цели:закрепить изученный материал в ходе решения задач; развивать логическое мышление учащихся.
Ход урока
I. Устная работа.
По заранее заготовленным чертежам на доске устно решить задачи:
1. На рисунке 1 ABCD – параллелограмм,O– точка пересечения диагоналей.
Выразите через векторы![]() и
и![]() векторы: а)
векторы: а)![]() б)
б)![]() гдеМ– точка на сторонеBC,
такая, чтоМВ : MC = 3 : 2; в)
гдеМ– точка на сторонеBC,
такая, чтоМВ : MC = 3 : 2; в)![]() гдеK– точка на сторонеAD, такая,
чтоАK :KD = 1 : 3; г)
гдеK– точка на сторонеAD, такая,
чтоАK :KD = 1 : 3; г)![]() гдеN – точка на диагоналиAC,
такая, чтоON = NC.
гдеN – точка на диагоналиAC,
такая, чтоON = NC.
2. На рисунке 2 ABCD – трапеция,О –
точка пересечения диагоналей,ВС ||
AD,AD = 2BC. Выразите через векторы![]() и
и![]() векторы: а)
векторы: а)![]() б)
б)![]()
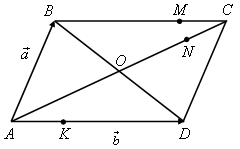
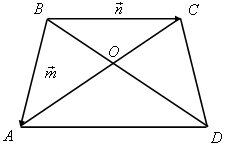
Рис. 1 Рис. 2
II. Решение задач.
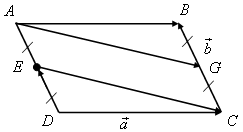
1. решить задачу № 782 на доске и в тетрадях.
|
Решение
Из треугольника ECD(рис. 3) найдем по правилу вычитания векторов: |
|
![]() тогда
тогда![]()
Из треугольника ABGпо правилу сложения векторов имеем
![]() отсюда
отсюда![]()
2. решить задачу № 802 на доске и в тетрадях.
III. Проверочная самостоятельная работа.
Вариант I
1. Начертите два неколлинеарных вектора
![]() и
и![]() так,
что
так,
что![]() = 3 см,
= 3 см,![]() = 2 см. Постройте
= 2 см. Постройте![]()
2. Четырехугольник KMNP – параллелограмм.
Выразите через векторы![]() и
и![]() векторы
векторы![]() и
и![]() ,
гдеА– точка на сторонеPN, такая,
чтоPA :AN = 2 : 1,B – середина
отрезкаMN.
,
гдеА– точка на сторонеPN, такая,
чтоPA :AN = 2 : 1,B – середина
отрезкаMN.
Вариант II
1. Начертите два неколлинеарных вектора
![]() и
и![]() так, что
так, что![]() = 2 см,
= 2 см,![]() = 3 см. Постройте вектор
= 3 см. Постройте вектор![]()
2. В параллелограмме ABCDточкаM– середина стороныCD;N– точка
на сторонеAD, такая, чтоAN:ND =
1 : 2. Выразите векторы![]() и
и![]() через векторы
через векторы![]() и
и![]() .
.
Вариант III (для более подготовленных учащихся)
1. В треугольнике ABCуголC= 90°,AC= 3 см,BC= 4 см. Постройте вектор![]()
2. В трапеции ABCDAB || CD,AB = 3CD.
Выразите через векторы![]() и
и![]() векторы
векторы![]() и
и![]() ,
гдеM – середина стороныBC, аN– точка на сторонеAB, такая, чтоAN
:NВ = 2 : 3.
,
гдеM – середина стороныBC, аN– точка на сторонеAB, такая, чтоAN
:NВ = 2 : 3.