IV. Итоги урока.

Домашнее задание:выучить материал пунктов 110–112; повторить материал пунктов 105–109; ответить на вопросы 1–12 на с. 290; решить задачи № 1121, 1128, 1124.

Урок 8 Решение задач

Цели:закрепить знания учащихся по изученной теме «Длина окружности и площадь круга»; научить учащихся применять изученные формулы при решении задач; развивать логическое мышление учащихся.

Ход урока

I. Актуализация опорных знаний учащихся.

1. Повторить определения окружности, круга, кругового сектора и кругового сегмента.

2. Записать на доске и в тетрадях формулы для вычисления длины окружности, длины дуги окружности; для вычисления площади круга, площади кольца, площади кругового сектора.

II. Решение задач.

1. Решить задачу № 1112.

Решение

l=∙;l= 24 см;= 38°. Найдем:R.

R=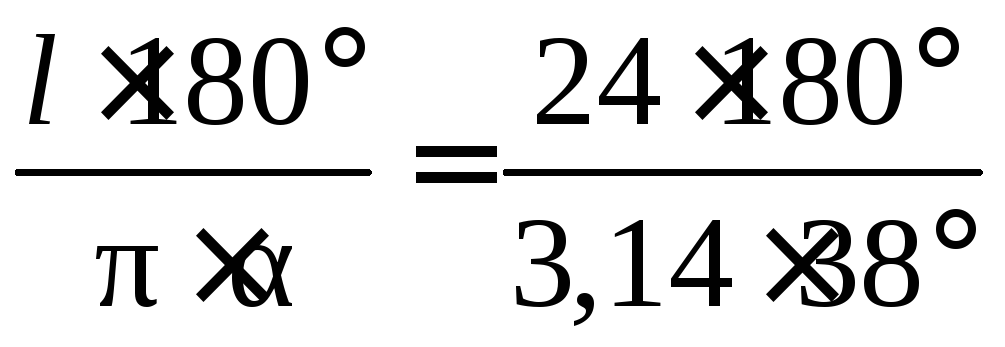≈ 36,3 (см).

ответ: ≈ 36,3 см.

2. Решить задачу № 1113 (самостоятельно).

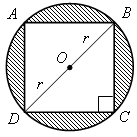
3. Решить задачу № 1123 на доске и в тетрадях.

Решение

АВСD– квадрат;DО=ОВ=r; Sкруга=πr2;Sквадрата=а2, ВD= 2r; изДВСDпо теореме Пифагора найдем сторону квадратаАВСD: а2+а2= (2r)2; 2а2= 4r2;а2= 2r2; тогдаSквадрата= 2r2.

Найдем площадь оставшейся части круга:

S=S_круга–S_{квадрата}=πr²– 2r²=r² (π– 2).

Ответ:r² (π– 2).

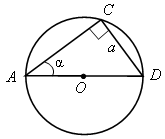
4. Решить задачу № 1116 (б).

Решение АСD– прямоугольный; А=,СD=а. АD= 2R(диаметр),АСD= 90° (вписанный угол, опирающийся на диаметр, прямой). Найдем АD.

Sin  =;AD =, тогда радиусRописанной около прямоугольного треугольника окружности равенR=AD =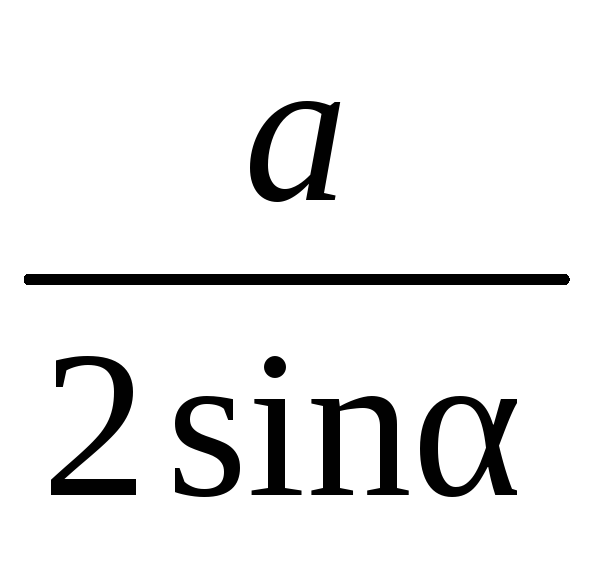. Площадь круга равнаS=πR²=.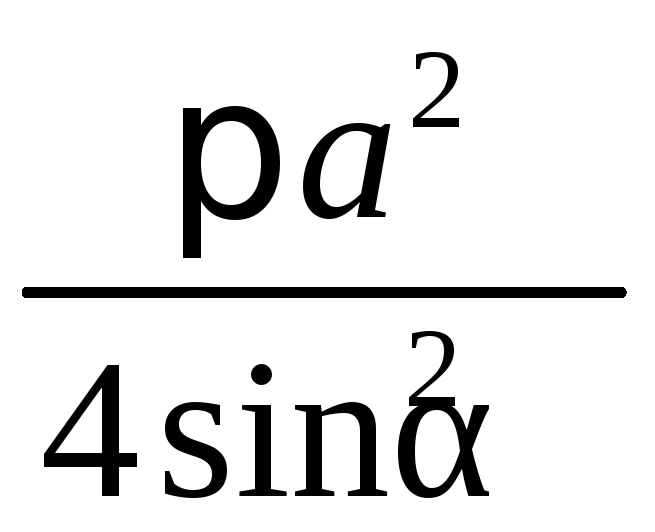

Ответ:.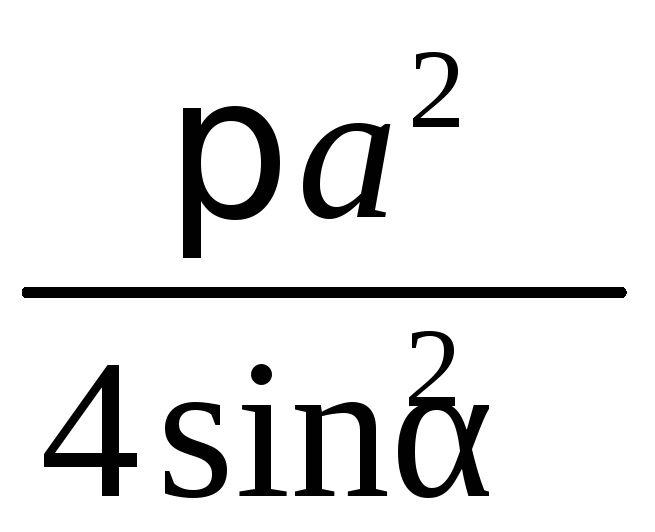

5. Решить задачи:

1) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 12 дм². Найдите радиусы окружностей, если один их них в два раза больше другого.

Ответ:дм;дм.

2) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см². Найдите площади этих кругов, ограниченных этими окружностями, если радиус одной из них в три раза больше, чем радиус другой.

Ответ: 1 см²и 9 см².

6. Решить задачу № 1108 (самостоятельно).

III. Самостоятельная работа (10–15 мин).

Вариант I

Решить задачи №№ 1102 (в), 1115 (б), 1109 (в), 1104 (б).

Вариант II

Решить задачи №№ 1102 (г), 1115 (а), 1109 (г), 1116 (а).

IV. Итоги урока.

Домашнее задание:повторить материал пунктов 105–112; решить задачи №№ 1107, 1132, 1137.

Уроки 9–10 Решение задач по материалу главы XII

Цели:закрепить знания и умения учащихся по изученному материалу главы; подготовить учащихся к контрольной работе.

Ход уроков

I. Математический диктант (15 мин).

Вариант I

1. Площадь круга равна S. Найдите длину ограничивающей его окружности.

2. Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 120°.

3. Длина дуги окружности равна 3π, а ее радиус равен 8. Найдите градусную меру этой дуги.

4. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

5. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45°.

6. Площадь кругового сектора равна 18πм², а его центральный угол равен 40°. Найдите радиус сектора.

Вариант II

1. Длина окружности равна С. Найдите площадь ограниченного ею круга.

2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 и 24 см.

3. Найдите площадь кругового сектора радиуса 3 см, если его центральный угол равен 20°.

4. Площадь кругового сектора равна 10πм², а его радиус равен 6 м. Найдите центральный угол сектора.

5. Найдите длину дуги окружности радиуса 6 дм, если ее градусная мера равна 120°.

6. Найдите радиус окружности, если длина дуги окружности равна 6π, а ее градусная мера равна 60°.