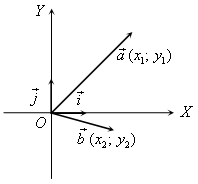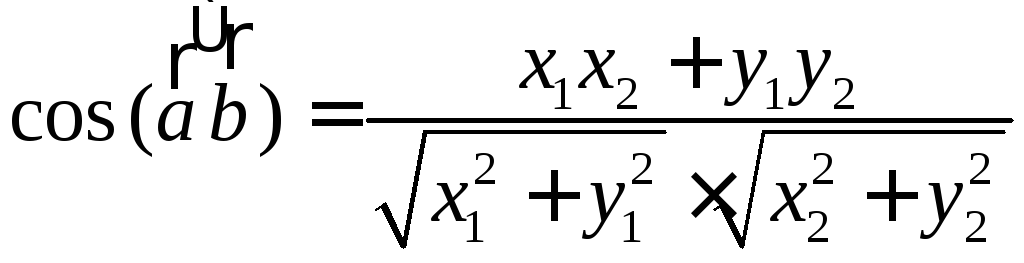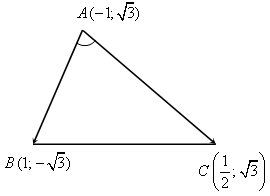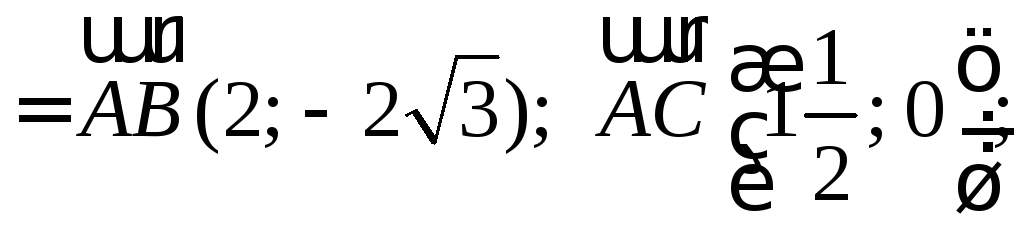- •Уроки 1–2 Повторение. Решение задач
- •Ход уроков
- •III. Итоги уроков.
- •Понятие вектора. Равенство векторов. (8 часов) Урок 1 Понятие вектора. Равенство векторов
- •Ход урока
- •III. Итоги урока.
- •Урок 2 Сумма двух векторов. Законы сложения векторов. Правило параллелограмма
- •Ход урока
- •I. Анализ результатов самостоятельной работы.
- •III. Выполнение практических заданий и упражнений.
- •IV. Итоги урока.
- •III. Закрепление изученного материала.
- •IV. Самостоятельная работа (обучающего характера).
- •III. Решение задач и упражнений.
- •IV. Проверочная самостоятельная работа.
- •V. Итоги урока.
- •Урок 5 Произведение вектора на число
- •Ход урока
- •II. Закрепление изученного материала.
- •II. Решение задач.
- •III. Проверочная самостоятельная работа.
- •IV. Итоги урока.
- •V. Итоги урока.
- •Урок 8 Средняя линия трапеции
- •Ход урока
- •I. Проверка усвоения учащимися материала.
- •II. Объяснение нового материала.
- •IV. Проверочная самостоятельная работа.
- •III. Изучение нового материала.
- •V. Итоги урока.
- •IV. Самостоятельная работа контролирующего характера.
- •1)Координаты середины отрезка.
- •2)Вычисление длины вектора по его координатам.
- •3) Расстояние между двумя точками.
- •IV. Итоги урока.
- •II. Решение задач.
- •III. Итоги урока.
- •Урок 5 Уравнение линии на плоскости. Уравнение окружности
- •Ход урока
- •II. Объяснение нового материала.
- •IV. Итоги урока.
- •III. Итоги урока.
- •Урок 7 Уравнение прямой
- •Ход урока
- •II. Изучение нового материала.
- •IV. Итоги урока.
- •Уроки 8–9 решение задач
- •Ход уроков
- •II. Решение задач.
- •III. Опрос учащихся по теоретическому материалу.
- •IV. Решение задач.
- •V. Итоги уроков.
- •III. Итоги урока.
- •IV. Итоги урока.
- •Урок 2 формулы приведения. Формулы для вычисления координат точки
- •Ход урока
- •II. Изучение нового материала.
- •IV. Итоги урока.
- •II. Объяснение нового материала.
- •IV. Итоги урока.
- •III. Решение задач.
- •IV. Итоги урока.
- •III. Решение задач.
- •III. Самостоятельная работа контролирующего характера.
- •IV. Итоги урока.
- •Урок 9 Угол между векторами. Скалярное произведение векторов
- •Ход урока
- •II. Объяснение нового материала.
- •Скалярное произведение векторов
- •II. Изучение нового материала.
- •Скалярное произведение в координатах
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Урок 11 Решение задач
- •Ход урока
- •II. Решение задач.
- •III. Устный опрос учащихся по карточкам.
- •IV. Итоги уроков.
- •Длина окружности. Площадь круга. (11 часов)
- •III. Изучение нового материала.
- •IV. Закрепление изученного материала.
- •II. Работа с учебником.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •III. Итоги урока.
- •Урок 5 Длина окружности
- •Ход урока
- •IV. Итоги урока.
- •Урок 6 Площадь круга
- •Ход урока
- •III. Итоги урока.
- •IV. Итоги урока.
- •IV. Итоги урока.
- •Уроки 9–10 Решение задач по материалу главы XII
- •Ход уроков
- •II. Решение задач.
- •III. Проверочная самостоятельная работа.
- •Движения. (8 часов)
- •III. Изучение нового материала.
- •IV. Закрепление изученного материала.
- •V. Итоги уроков.
- •Урок 4 Параллельный перенос
- •Ход урока
- •I. Проверка изученного материала.
- •II. Изучение нового материала.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Уроки 5–6 Поворот
- •Ход уроков
- •III. Закрепление изученного материала.
- •V. Итоги уроков.
- •Урок 8 Контрольная работа № 4
- •Ход урока
- •I. Организация учащихся на выполнение работы.
- •II. Выполнение работы по вариантам.
- •Начальные сведения из стереометрии (7 часов) Урок 1 Предмет стереометрии. Многогранник
- •Ход урока
- •I. Изучение нового материала.
- •II. Закрепление изученного материала.
- •III. Итоги урока.
- •Урок 2 Призма. Параллелепипед
- •Ход урока
- •I. Устная работа.
- •II. Объяснение нового материала.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Урок 3 Объем тела. Свойства прямоугольного параллелепипеда
- •Ход урока
- •I. Проверка домашнего задания.
- •II. Изучение нового материала.
- •III. Выполнение упражнений и решение задач.
- •IV. Итоги урока.
- •Урок 4 Пирамида
- •Ход урока
- •I. Актуализация опорных знаний учащихся.
- •II. Работа учащихся по учебнику.
- •III. Выполнение упражнений. Решение задач.
- •IV. Итоги урока. Выставление оценок.
- •Урок 5 Цилиндр
- •Ход урока
- •I. Объяснение нового материала.
- •II. Закрепление изученного материала.
- •III. Итоги урока.
- •III. Выполнение упражнений.
- •IV. Итоги урока.
- •Урок 7 Сфера и шар
- •Ход урока
- •II. Работа с учебником.
- •III. Закрепление изученного материала.
- •IV. Итоги урока.
- •Об аксиомах и планиметрии (2 часа)
- •Решение задач
- •Треугольник
- •Окружность
- •Четырехугольники. Многоугольники
- •Векторы. Метод координат. Движения
- •Литература
II. Изучение нового материала.
1. Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов.
2. Изучение теоремы о скалярном произведении векторов в координатах и свойств скалярного произведения полезно построить так, чтобы учащиеся сами проводили алгебраические преобразования.
Полученные результаты можно записать в тетради и вынести в настенную таблицу:
Скалярное произведение в координатах
|
|
|
Свойства скалярного произведения векторов:
1)
![]() ≥
0 (
≥
0 (![]() > 0 при
> 0 при![]()
![]() 0); 2)
0); 2)![]() ;
;
3)
![]() ;
4)
;
4)![]() .
.
III. Закрепление изученного материала.
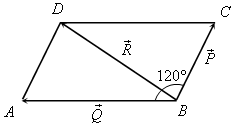
1. Решить задачу № 1043(объясняет учитель):
|
|
Дано:
Найти: Решение Пусть
|
![]() ,
тогда по правилу треугольника
,
тогда по правилу треугольника![]() (или по правилу параллелограмма вектор
(или по правилу параллелограмма вектор![]() есть равнодействующая сила
есть равнодействующая сила![]() ).
).
![]() C= 180° – 120° = 60° (сумма односторонних углов
равна 180°). По теореме косинусов из
треугольникаВСDнайдемВD:
C= 180° – 120° = 60° (сумма односторонних углов
равна 180°). По теореме косинусов из
треугольникаВСDнайдемВD:
BD2=BC2+CD2– 2BC∙CD∙ cosC=
= 82+ 152– 2 ∙ 8 ∙ 15 ∙![]() = 64 + 225 – 120 = 169;
= 64 + 225 – 120 = 169;
![]() =
169;
=
169;![]() =
13.
=
13.
Ответ: 13.
2. Решить задачи № 1044 (а, б).
3. Устно № 1045.
4. Решить задачи № 1046, 1047 (б, в) на доске и в тетрадях.
5. Решить задачу № 1051.
Решение
![]()
= 1 ∙ 2 cos 60° + 2 ∙ 2 cos 60° = 2 ∙
![]() + 4 ∙
+ 4 ∙![]() = 1 + 2 = 3.
= 1 + 2 = 3.
Ответ: 3.
6. Решить задачу № 1049 на доске и в тетрадях(для угла А объясняет учитель):
Решение
|
|
1) cos A=
|
![]()
![]()
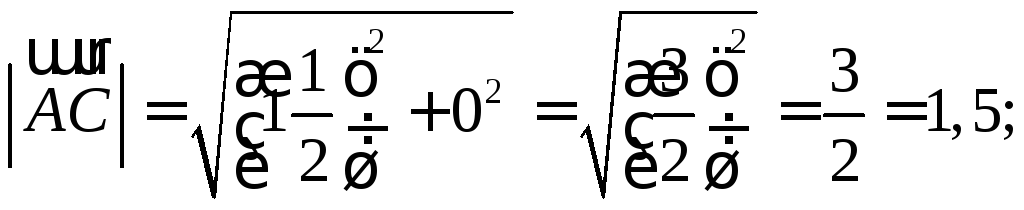
cos A
= 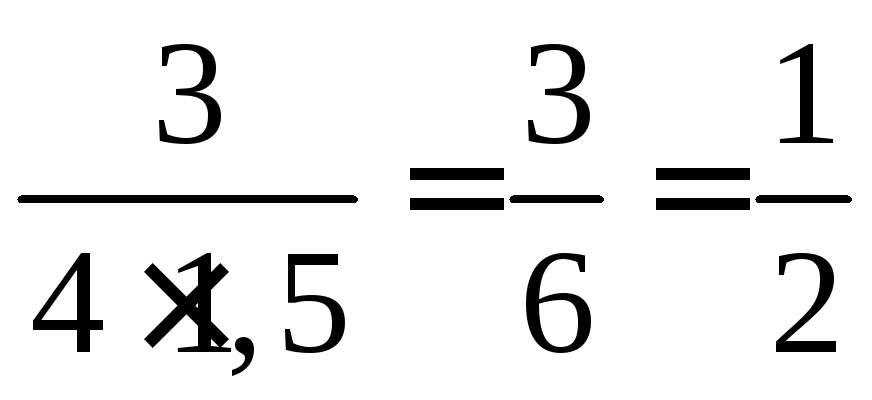 ;
cos A =
;
cos A =
![]() ,
то
,
то ![]() A
= 60°.
A
= 60°.
2) cos B=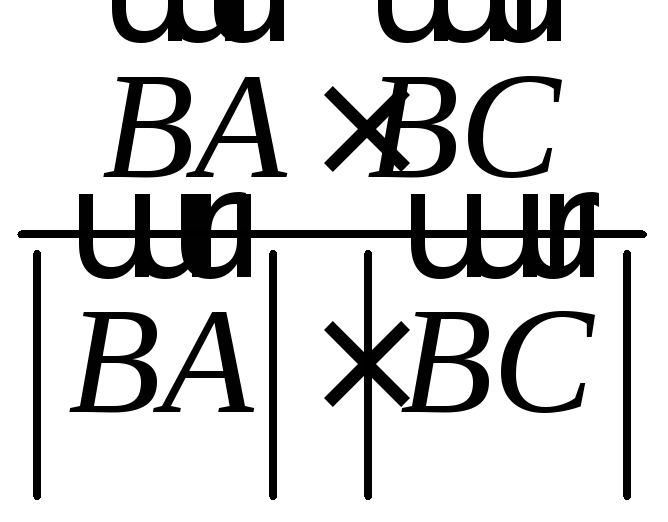 ;
;![]()
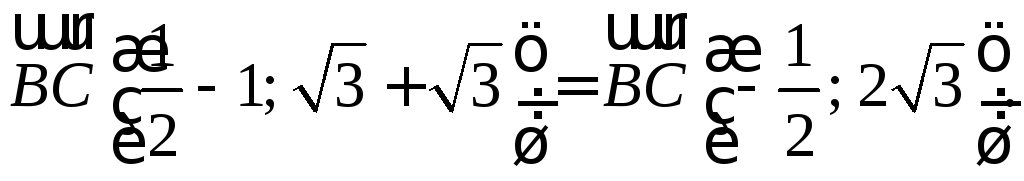
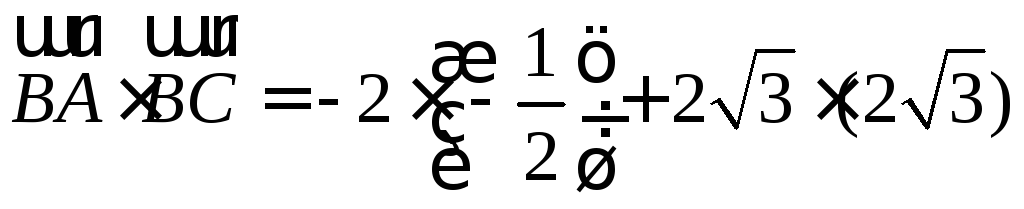 =
1 + 12 = 13;
=
1 + 12 = 13;
![]()
BC=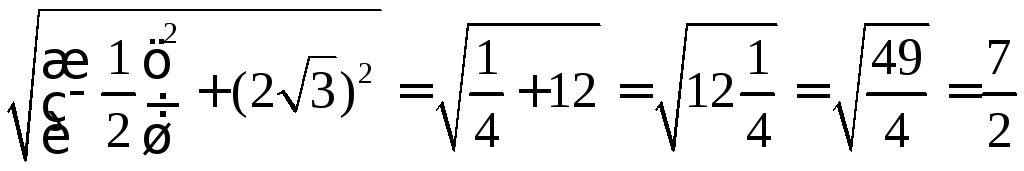 =
3,5;
=
3,5;
cos B=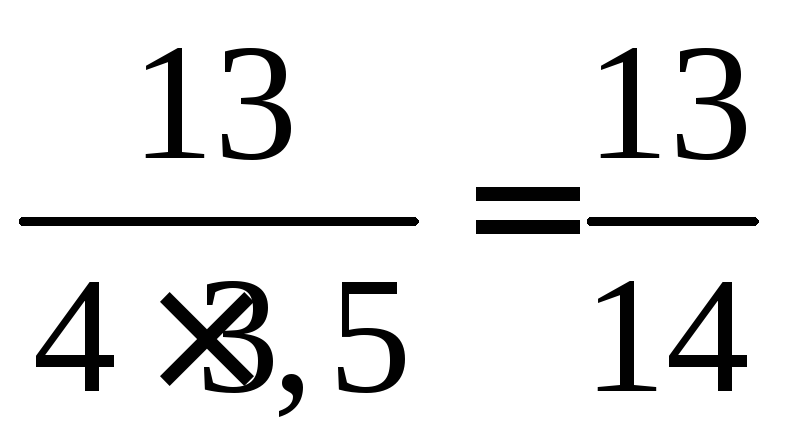 ≈
0,9286;
≈
0,9286;![]() Bнаходим по таблицам Брадиса:
Bнаходим по таблицам Брадиса:
![]() B
≈ 21°47′.
B
≈ 21°47′.
3) ![]() C
= 180° – 60° – 21°47′ ≈ 98°13′.
C
= 180° – 60° – 21°47′ ≈ 98°13′.
Ответ:
![]() A
= 60°;
A
= 60°; ![]() B
≈ 21°47′;
B
≈ 21°47′; ![]() C
≈ 98°13′.
C
≈ 98°13′.
7. Решить задачу № 1052.
Решение
![]()
![]() =
52– 2 ∙ 5 ∙ 2 cos 90° + 22– 42=
=
52– 2 ∙ 5 ∙ 2 cos 90° + 22– 42=
= 25 + 4 – 16 = 13;
![]() =
13.
=
13.
Ответ: 13.
8. Решить задачу № 1066.
Решение
По условию
![]() .
.
![]()
![]() =
9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.
=
9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.
![]() =
25, тогда
=
25, тогда![]() = 5.
= 5.
Ответ: 5.
IV. Итоги урока.
Домашнее задание: изучить материал пунктов 101–104; ответить на вопросы 17–20 на странице 271 учебника; решить №№ 1044 (в), 1047 (а), 1054 (разобрать решение задачи и записать в тетрадь).
Урок 11 Решение задач
Цели:закрепление и проверка знаний и умений учащихся, сформированных при изучении главы XI, формирование навыков решения задач, развитие навыков логического мышления.
Ход урока
I. Математический диктант (10 мин).
Вариант I
1. Вычислите скалярное произведение
векторов
![]() и
и![]() ,
если
,
если![]() ,
а угол между ними равен 120°.
,
а угол между ними равен 120°.
2. Скалярное произведение ненулевых
векторов
![]() и
и![]() равно 0. Определите угол между векторами
равно 0. Определите угол между векторами![]() и
и![]() .
.
3. Вычислите скалярное произведение
векторов
![]() и
и![]() ,
если
,
если![]() (3;
–2),
(3;
–2),![]() (–2;
3).
(–2;
3).
4. Найдите угол между ненулевыми векторами
![]() (х;у) и
(х;у) и![]() (–у;х).
(–у;х).
5. Вычислите косинус угла между
векторами
![]() и
и![]() ,
если
,
если![]() (3;
–4),
(3;
–4),![]() (15;
8).
(15;
8).
6. Даны векторы
![]() (2;
–3) и
(2;
–3) и![]() (х;
–4). При каком значениихэти векторы
перпендикулярны?
(х;
–4). При каком значениихэти векторы
перпендикулярны?
Вариант II
1. Вычислите скалярное произведение
векторов
![]() и
и![]() ,
если
,
если![]() ,
а угол между ними равен 135°.
,
а угол между ними равен 135°.
2. Скалярное произведение ненулевых
векторов
![]() и
и![]() равно нулю. Определите угол между этими
векторами.
равно нулю. Определите угол между этими
векторами.
3. Вычислите скалярное произведение
векторов
![]() и
и![]() ,
если
,
если![]() (–4;
5),
(–4;
5),![]() (–5;
4).
(–5;
4).
4. Найдите угол между ненулевыми векторами
![]() (х;
–у) и
(х;
–у) и![]() (у;х).
(у;х).
5. Вычислите косинус угла между
векторами
![]() и
и![]() ,
если
,
если![]() (–12;
5),
(–12;
5),![]() (3;
4).
(3;
4).
6. Даны векторы
![]() (3;у) и
(3;у) и![]() (2;
–6). При каком значенииуэти векторы
перпендикулярны?
(2;
–6). При каком значенииуэти векторы
перпендикулярны?