III. Самостоятельная работа контролирующего характера.
Вариант I
Решить задачи №№ 1060 (а); 1058 (б); 1061 (а).
Вариант II
Решить задачи №№ 1060 (б); 1058 (а); 1061 (б).
IV. Итоги урока.
Домашнее задание:повторить тему «Векторы», материал пунктов 76–85 и 86–89; решить задачи №№ 1024, 1035.
Урок 9 Угол между векторами. Скалярное произведение векторов
Цели:познакомить учащихся с понятием угла между векторами; ввести скалярное произведение векторов; рассказать о применении скалярного произведения векторов в физике, механике; развивать логическое мышление учащихся.
Ход урока
I. Математический диктант (15 мин).
Вариант I
1. Диагонали параллелограмма АВСDпересекаются в точкеО.какие
векторы коллинеарны вектору
?
2. Диагонали параллелограмма АВСDпересекаются в точкеО. Какие векторы
сонаправлены с вектором
?
3. Диагонали параллелограмма АВСDпересекаются в точкеО. Какие векторы
равны вектору
?
4. При каком условии
?
5. Известно, что
= 3,
= 4. Найдите
,
еслиАОВD– прямоугольник.
6. В треугольнике СDЕDЕ= 5,СЕ= 4, уголС= 45°. Найдите сторонуDЕ.
7. В треугольнике КLM КL = LМ = 5, КМ = 6. Найдите косинус угла L.
8. В треугольнике ОРQуголО= 60°, уголР= 75°,ОР= 8. Найдите сторонуРQ.
Вариант II
1. Диагонали ромба КLМРпересекаются
в точкеТ. Какие векторы коллинеарны
вектору
?
2. Диагонали ромба КLМРпересекаются
в точкеТ.какие
векторы сонаправлены с вектором
?
3. Диагонали ромба КLМРпересекаются
в точкеТ. Какие векторы равны вектору
?
4. При каком условии
?
5. Известно, что точки СиDлежат
соответственно на осяхОХиОYпрямоугольной системы координат. Найдите
,
если
= 5,
= 12.
6. В треугольнике АВС АВ = ВС = 8,АС= 4. Найдите косинус углаА.
7. В треугольнике ВСD ВС = 6, уголВ= 75°, уголС= 45°. Найдите сторонуВD.
8. В треугольнике DЕF DЕ = 6, ЕF = 7, уголЕ= 30°. Найдите сторонуDF.
II. Объяснение нового материала.
1. Ввести понятие
угла между векторами
и
(рис. 300 и таблица).
2. Угол между
векторами
и
не зависит от выбора точкиО, от
которой откладываются векторы
и
.
3. Угол между сонаправленными векторами считается равным нулю.
4. Обозначение угла
между векторами:
.
5. Определение углов между векторами на рисунке 301.
6. Определение перпендикулярных векторов.
7. Повторить по настенным таблицам сложение и вычитание векторов, умножение вектора на число.
8. Введение еще одного действия над векторами –скалярного умножения векторов. В отличие от суммы и разности векторов скалярное произведение есть число (скаляр) – именно это и обусловило название операции.
9. В тетрадях учащиеся оформляют таблицу:
Скалярное произведение векторов
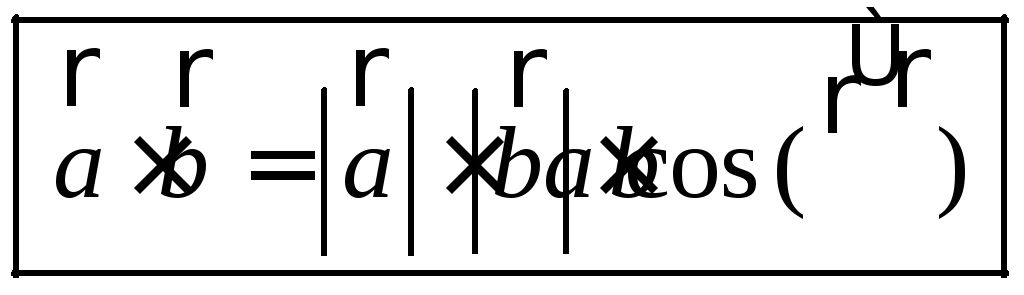
Если
и
,
то
а) (0 ≤
<
90°) <=> (
> 0); б) (90° <
≤
180°) <=> (
<
0);
в)
<=> (
= 0); г) (
=
0°) <=>
.
10. Скалярное произведение векторов
широко используется в физике. Например,
из курса механики известно, что работа
Апостоянной силы
при перемещении тела из точкиМв
точкуN(рис. 303) равна произведению
длин векторов силы
и перемещения
на косинус угла между ними:
.
III. Закрепление изученного материала.
1. Решить задачи №№ 1039 (а, б, ж, з) и 1040 (а, д, е) по готовым чертежам квадрата и ромба, заранее выполненным на доске.
2. Решить задачу № 1041 (в).
Примечание.Сos
135° = cos (180° – 45°) = – cos 45° =
.
IV. Итоги урока.
Домашнее задание:изучение материалов пунктов 101 и 102; повторить материал п. 87; решить задачи №№ 1039 (в, г), 1040 (г), 1042 (а, б).
Урок 10 Скалярное произведение в координатах. Свойства скалярного произведения векторов
Цели:ввести понятие скалярного произведения в координатах; изучить свойства скалярного произведения векторов и закрепить их знание при решении задач.
Ход урока
I. Проверочная работа(10 мин).
Вариант I
1. Известно, что
,
где
и
– координатные векторы. Выпишите
координаты вектора
.
2. Дан вектор
(0;
5). Запишите разложение вектора
по координатным векторам
и
.
3. Даны векторы
(–1;
2) и
(2;
1). Найдите координаты суммы векторов
и
.
4. Найдите координаты вектора
,
если
(–3;
0).
5. Даны векторы
(5;
6) и
(–2;
3). Найдите координаты вектора
.
6. Две стороны треугольника равны 7 и 3 см, а угол между ними равен 120°. Найдите третью сторону треугольника.
7. втреугольникеАВСуголА= 45°,АВ= 2,АС= 3. Вычислите
.
8. Скалярное произведение ненулевых
векторов
и
равно нулю. Чему равен угол между
векторами
и
?
Вариант II
1. Дан вектор
(3;
0). Запишите разложение вектора по
координатным векторам
и
.
2. Известно, что
,
где
и
– координатные векторы. Выпишите
координаты вектора
.
3. Найдите координаты вектора –
,
если
(0; –2).
4. Даны векторы
(2;
–1) и
(3;
–1). Найдите координаты разности векторов
и
.
5. Даны векторы
(–1;
9) и
(3;
–2). Найдите координаты вектора
.
6. В треугольнике МРQуголM= 135°;МР= 5,МQ= 2
.
Вычислите
.
7. Две стороны треугольника равны 3 и 9 м, а угол между ними равен 60°. Найдите третью сторону треугольника.
8. Чему равно скалярное произведение
координатных векторов
и
?