
- •Лекция 2. Понятие кривой. Гладкие кривые. Канонический репер. Формулы Серре-Френе §2. Понятие кривой
- •§3. Гладкие кривые
- •§4. Касательная к кривой
- •§5. Длина кривой
- •§6. Канонический репер
- •§7. Формулы Серре-Френе
- •Лекция 3. Понятие поверхности. Гладкие поверхности. Координатная сеть на поверхности. Касательная плоскость и нормаль к поверхности §8. Векторная функция двух скалярных аргументов
- •§9. Понятие поверхности
- •§10. Кривые на поверхности
- •§11. Касательная плоскость и нормаль к поверхности
- •Лекция 4. Первая и вторая квадратичная форма поверхности §12. Первая квадратичная форма поверхности
- •§13. Вторая квадратичная форма поверхности. Кривизна линий на поверхности
- •§14. Индикатриса Дюпена
- •Лекция 5. Понятие внутренней геометрии поверхностей §15. Главные направления на поверхности. Полная и средняя кривизна поверхности. Формула Эйлера
- •§16. Внутренняя геометрия поверхности
- •Раздел IX. Основания геометрии
- •Лекция 1. Род структур. Основные математические структуры курса геометрии §1. Род структур
- •§2. Основные математические структуры курса геометрии
- •Лекция 2. Теория рода структур. Модель системы аксиом. Основные свойства системы аксиом §3. Теория рода структур
- •§4. Модель системы аксиом
- •§5. Основные свойства системы аксиом
- •Лекция 3. Основные этапы истории развития геометрии. «Начала» Евклида. Проблема пятого постулата и ее решение §6. Основные этапы истории развития геометрии. «Начала» Евклида
- •Лекция 4. Система аксиом Гильберта евклидовой геометрии §7. Обзор аксиоматики Гильберта евклидовой геометрии
- •I. Аксиомы принадлежности.
- •II. Аксиомы порядка.
- •III. Аксиомы конгруэнтности.
- •IV. Аксиомы непрерывности.
- •Лекция 5. Аксиоматика плоскости Лобачевского. Элементарные теоремы планиметрии Лобачевского §8. Независимость аксиомы параллельных от остальных аксиом евклидовой геометрии
- •§9. Элементарные теоремы геометрии Лобачевского
- •§10. Взаимное расположение прямых на плоскости Лобачевского
- •Лекция 6. Определение длины отрезка. Понятие площади плоской фигуры.
- •§11. Длина отрезка как результат процесса измерения
- •§12. Определение длины отрезка на основе расстояния между точками
- •§13. Аксиоматическое определение длины отрезка
- •§14. Площадь многоугольной фигуры
- •§15. Расширение класса квадрируемых фигур
- •Лекция 7. Величина и её измерение §16. Измерение объемов многогранных тел
- •§17. Расширение класса кубируемых фигур
- •§18. Понятие величины и её измерение
- •Литература
§2. Основные математические структуры курса геометрии
Структура поля действительных чисел.
База:
![]() −множество,
элементы которого называются
действительными числами.
−множество,
элементы которого называются
действительными числами.
Отношения:
Тернарное отношение
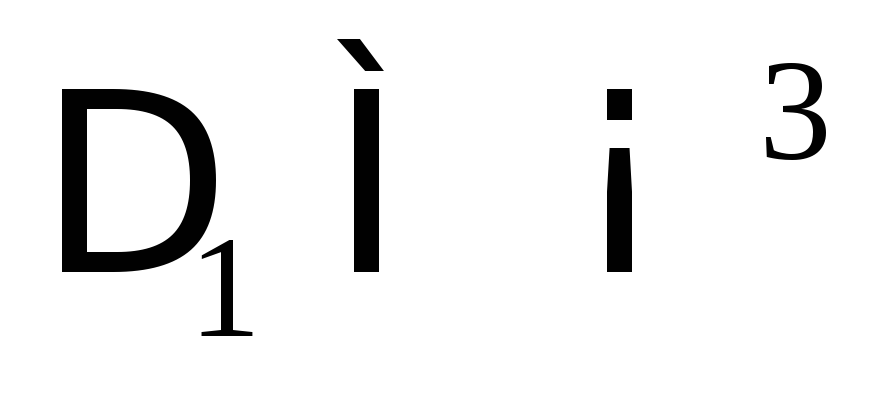 ,
определяющее бинарную алгебраическую
операцию − сложение, обозначаемую
символом
,
определяющее бинарную алгебраическую
операцию − сложение, обозначаемую
символом .
.
Если
![]() ,
то
,
то![]() .
.
Тернарное отношение
 ,
определяющее бинарную алгебраическую
операцию − умножение, обозначаемую
символом .
,
определяющее бинарную алгебраическую
операцию − умножение, обозначаемую
символом .
Если
![]() ,
то .
,
то .
Бинарное отношение
 ,
− отношение предшествования, обозначаемое
символом
,
− отношение предшествования, обозначаемое
символом .
Если
.
Если ,
то будем записывать
,
то будем записывать и называть число
и называть число меньшим числа , а число большим числа
меньшим числа , а число большим числа .
.
Аксиомы:
![]()
![]()
(аксиома непрерывности).
Структура n-мерного векторного пространства над полем .
База:
![]() − множество векторов,
− множество векторов,![]() − поле действительных чисел.
− поле действительных чисел.
Отношения:
Тернарное отношение
 ,
определяющее бинарную алгебраическую
операцию − сложение векторов, обозначаемую
символом +.
,
определяющее бинарную алгебраическую
операцию − сложение векторов, обозначаемую
символом +.
Если
![]() то
то![]() .
.
Тернарное отношение , определяющее умножение вектора на число, обозначаемое постановкой числа и вектора рядом.
Если
![]() ,
то
,
то![]() .
.
Аксиомы:
.
.
.
.
.
.
.
.
Существует базис из векторов.
Структура n-мерного евклидова векторного пространства над полем .
Добавим
к отношениям структуры n-мерного
векторного пространства тернарное
отношение, определяющее отображение
![]() ,
называемое скалярным умножением
векторов, обозначаемое символом
,
называемое скалярным умножением
векторов, обозначаемое символом![]() в соответ-ствии с равенством
в соответ-ствии с равенством![]() ,
и удовлетворяющее аксиомам:
,
и удовлетворяющее аксиомам:
.
.
 .
.
Структура n-мерного аффинного пространства.
База:
![]()
![]() множество
точек,
множество
точек,
![]() –n-мерное
векторное пространство над полем
–n-мерное
векторное пространство над полем
![]() действительных чисел, называемое
пространством переносов.
действительных чисел, называемое
пространством переносов.
Отношения:
Тернарное
отношение
![]() ,
определяющее
,
определяющее
отображение
![]() .
Если
.
Если![]() ,
то условимся обозначать
,
то условимся обозначать![]() .
.
Аксиомы:
К аксиомам n-мерного векторного пространства добавляются две аксиомы Вейля.
![]()
![]()
Структура евклидова n-мерного точечного пространства.
Если к
отношениям и аксиомам структуры
![]() -мерного
аффинного пространства добавить
отношения и аксиомы, которые делают
пространство переносов евклидовым
векторным пространством, то получим
структуру евклидова
-мерного
аффинного пространства добавить
отношения и аксиомы, которые делают
пространство переносов евклидовым
векторным пространством, то получим
структуру евклидова![]() -мерного
точечного пространства.
-мерного
точечного пространства.
Структура проективного пространства.
База:
![]() –множество
точек,
–множество
точек,
![]() – векторное пространство размерности
– векторное пространство размерности![]() ,
,![]() –поле действительных чисел.
–поле действительных чисел.
Отношения:
Бинарное
отношение
![]() ,
определяющее отображение
,
определяющее отображение![]() .
Если
.
Если![]() ,
то будем говорить, что вектор
,
то будем говорить, что вектор![]() порождает точку
порождает точку![]() и записывать
и записывать![]() .
.
Аксиомы:
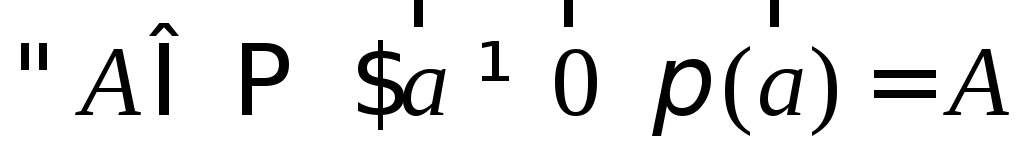 ,
то есть π сюръективно.
,
то есть π сюръективно. .
.
Структура метрического пространства.
База:
![]() –непустое
множество,
–непустое
множество,
![]() – поле действительных чисел.
– поле действительных чисел.
Отношения:
Тернарное
отношение
![]() ,
определяющее отображение
,
определяющее отображение![]() .
Если
.
Если![]() ,
то будем говорить, что
,
то будем говорить, что![]() – расстояние от
– расстояние от![]() до
до![]() .
.
Аксиомы:

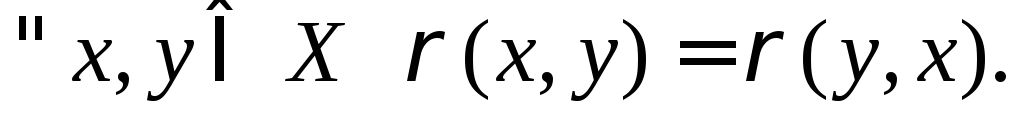
(аксиома «треугольника»).
Структура топологического пространства.
База:
![]() –множество
точек.
–множество
точек.
Отношения:
Унарные
отношения
![]() на
множестве
на
множестве![]() .
.
Подмножества
![]() условно
называютсяоткрытыми.
условно
называютсяоткрытыми.
Совокупность
![]() всех открытых множеств называетсятопологией
пространства.
всех открытых множеств называетсятопологией
пространства.
Аксиомы:


 .
.
Лекция 2. Теория рода структур. Модель системы аксиом. Основные свойства системы аксиом §3. Теория рода структур
Математика
занимается изучением математических
структур. Основным ее методом является
аксиоматический
метод:
структура каждого рода определяется
при помощи соответствующей системы
аксиом
![]() ,
а дальше логическим путем строится
теория
структур этого рода – совокупность
предложений, каждое из которых является
либо аксиомой, либо выводится из
высказываний, полученных ранее, при
,
а дальше логическим путем строится
теория
структур этого рода – совокупность
предложений, каждое из которых является
либо аксиомой, либо выводится из
высказываний, полученных ранее, при
помощи принятых в математической логике правил вывода.
Так, мы имеем теорию групп, теорию колец, теорию (геометрию) аффинного, евклидова, проективного пространства, и т.д.
Если
в теориях
![]() и
и![]() двух родов структур все понятия и
отношения каждого из этих родов структур
можно определить как основные или
производные понятия и отношения другого
рода структур и при этом все аксиомы
каждой из этих теорий будут аксиомами
или теоремами другой теории, то говорят,
что этидве
теории совпадают.
Системы аксиом ∑ и
двух родов структур все понятия и
отношения каждого из этих родов структур
можно определить как основные или
производные понятия и отношения другого
рода структур и при этом все аксиомы
каждой из этих теорий будут аксиомами
или теоремами другой теории, то говорят,
что этидве
теории совпадают.
Системы аксиом ∑ и
![]() этих родов структур называютсяэквивалентными.
этих родов структур называютсяэквивалентными.
