
- •По специальности 1-40 01 01 «Программное обеспечение информационных технологий»
- •Математический анализ
- •Геометрия и алгебра
- •Современные главы высшей математики
- •Теория вероятностей и математическая статистика
- •Дифференциальные уравнения
- •Начертательная геометрия, инженерная и машинная графика
- •Основы алгоритмизации и программирования
- •Объектно-ориентированное программирование
- •Базы данных
- •Операционные системы и системное программирование
- •Структура и организация данных
- •Объектно-ориентированное программирование
- •Базы данных
- •Операционные системы и системное программирование
- •Защита информационных ресурсов компьютерных систем и сетей
- •Надежность программного обеспечения
- •Технология разработки по
- •Организация производства и управления предприятием
- •Языки программирования
- •Структура и организация данных
- •Компьютерные системы и сети
- •Перечень задач Математический анализ
- •Геометрия и алгебра
- •Теория вероятностей и математическая статистика
- •Дифференциальные уравнения
- •Базы данных
- •Для базы данных, состоящей из таблиц
- •Для базы данных, состоящей из таблиц
Перечень задач Математический анализ
Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми
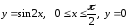 .
.
Найти площадь фигуры, ограниченной криыми
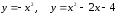 .
.
Вычислить интеграл
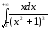
Исследовать на экстремум функцию
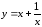 .
.
Найти область сходимости степенного ряда
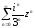 .
.
Найти сумму ряда

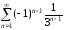 .
.
Вычислить интеграл
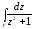 где
где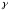 -
окружность: а)
-
окружность: а)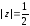 ;
;
б)
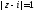 .
.
Функцию
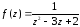 разложить в ряд Лорана в кольце
разложить в ряд Лорана в кольце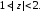
Геометрия и алгебра
Решите матричным методом систему линейных уравнений
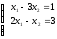
Пользуясь схемой Горнера разложить многочлен f(x) по степеням x-5 и вычислите f (b), если: f (x) = x4 – 3x3 + 6x2 – 10x + 16, b = 5;
Найдите разложение вектора
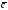 по векторам
по векторам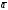 и
и
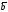 :
:
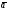 (4,
– 2),
(4,
– 2),
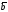 (3,5),
(3,5),
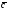 (1,
– 7);
(1,
– 7);
Докажите, что фигура, ограниченная прямыми x– 3y + 1 = 0,
x – 3y + 12 = 0, 3x + y – 1 = 0, 3x + y + 10 = 0, – квадрат.
Вычислите его площадь.
Найдите точку, симметричную точке P (6, – 5, 5) относительно плоскости
2x – 3y + z – 4 = 0.
Исследуйте, являются ли данные векторы 1, sin2 x, cos2 x линейно зависимыми.
В случае утвердительного ответа найдите нетривиальную линейную комбинацию, равную 0.
Линейный оператор f в базисе е1, е2 имеет матрицу
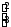
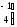 .
.
Найдите его матрицу в базисе а1 = 2е1- е2, а2 = е1+ 2е2.
Убедитесь, что векторы а1, а2 ортогональны, и дополните систему а1, а2
до ортогонального базиса, если:
а1 (1, – 2, 2, – 3), а2 (2, – 3, 2, 4)
Найдите расстояние между параллельными плоскостями:
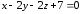 и
и
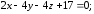
Найдите базис ядра линейного оператора
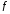 пространства
пространства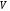 ,
заданного в некотором базисе матрицейА:
,
заданного в некотором базисе матрицейА:
А
=
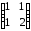
Теория вероятностей и математическая статистика
В коробке 6 деталей, причём 3 из них окрашены. Наудачу извлечены 2 детали. Найти вероятность того, что среди двух извлеченных деталей окажутся: а) одна окрашенная; б) 2 окрашенные; в) хотя бы одна окрашенная деталь.
Произведено 4 независимых испытания, в каждом из которых вероятность появления события А равна 0,6. Найти вероятность того, что событие А появится хотя бы 2 раза.
Имеются 2 урны, в одной находятся 2 черных и 2 белых шара, а в другой – 5 белых и 1 черный шар. Из взятой наудачу урны извлечен белый шар. Какова вероятность, что шар извлечен из урны, содержащей 5 белых шаров?
На отрезок АВ длины 5 наудачу брошены 4 точки. Найти вероятность того, что 3 точки будут находится от точки А на расстоянии, меньшем 1, а одна – на расстоянии, не меньшем 1.
На отрезке длиной 6 наудачу выбраны 2 точки. Найти вероятность, что сумма расстояний до левого конца превзойдет 4.
В партии из 5 деталей имеются 2 стандартных. Наудачу отобраны две детали. Составить ряд распределения, найти математическое ожидание и дисперсию числа стандартных деталей среди отобранных.
Случайная величина Х имеет плотность распределения
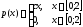 .
.
Найти параметр С, функцию распределения и математическое ожидание случайной величины Х.
