Задачи контрольной работы

В заданиях 4.2.1 – 4.2.20 найти указанные пределы.

.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.

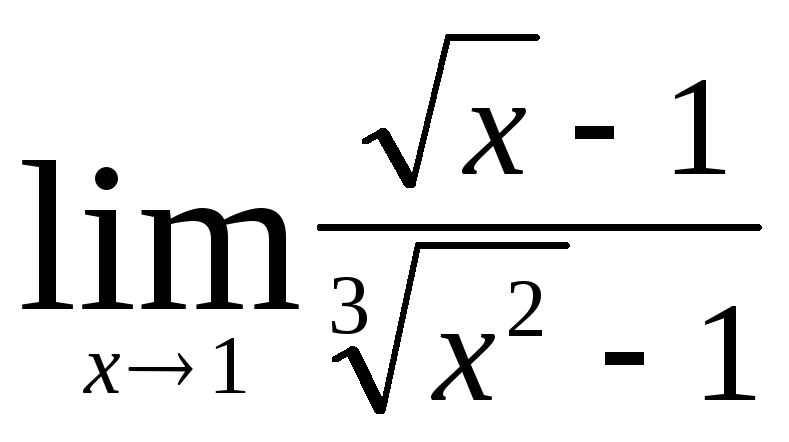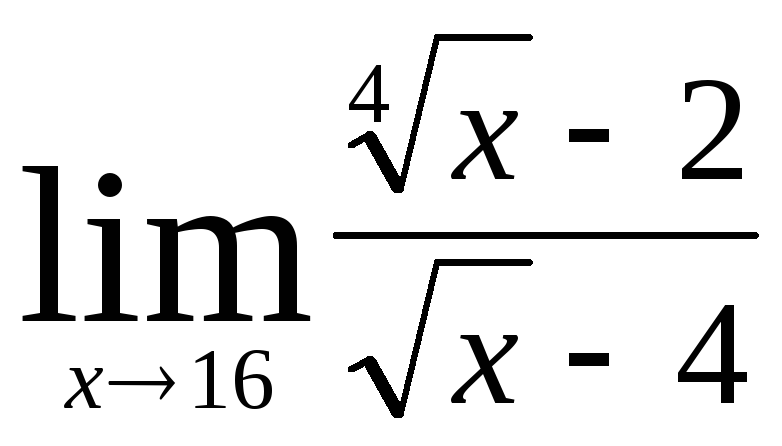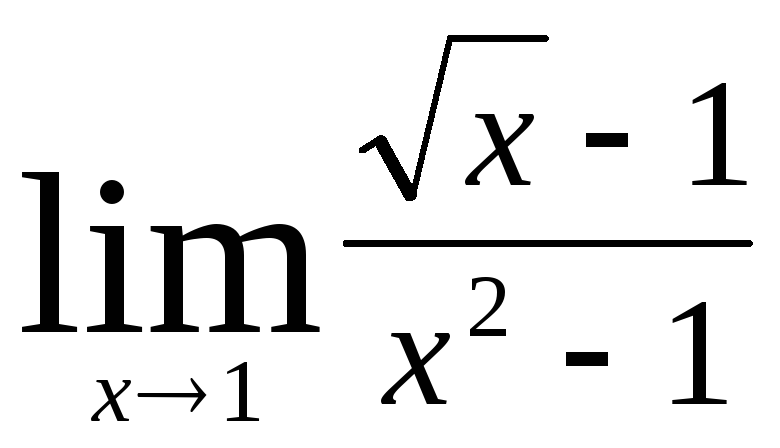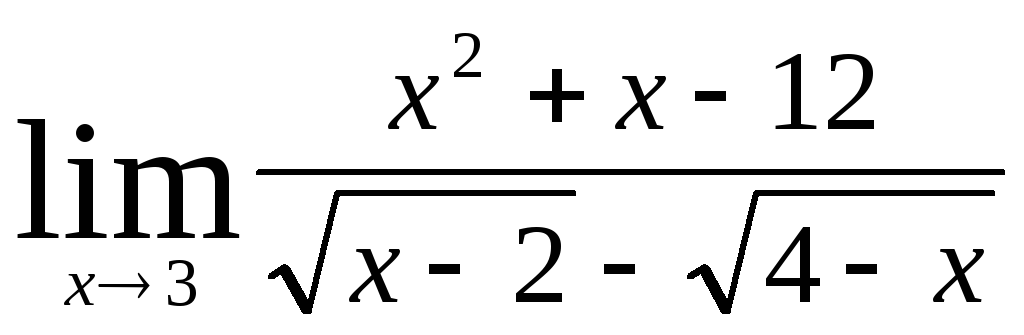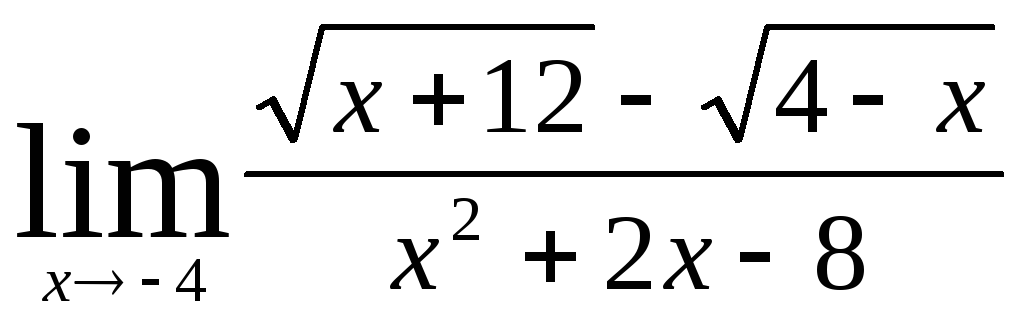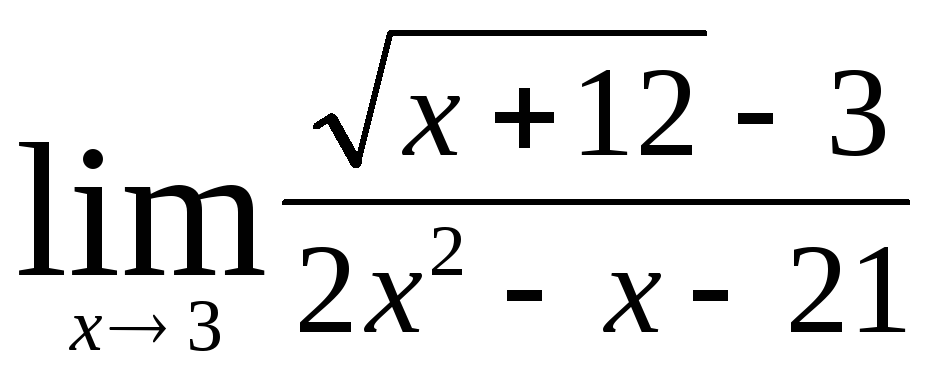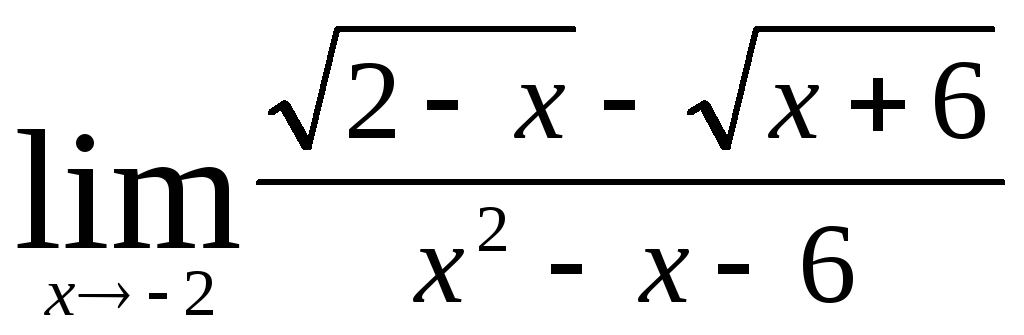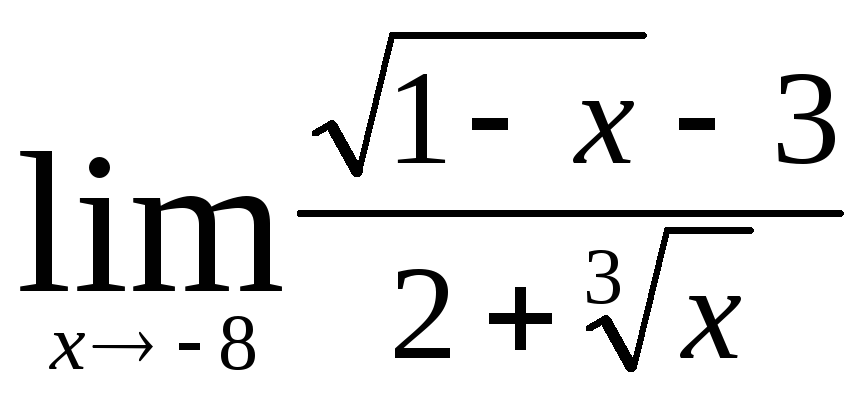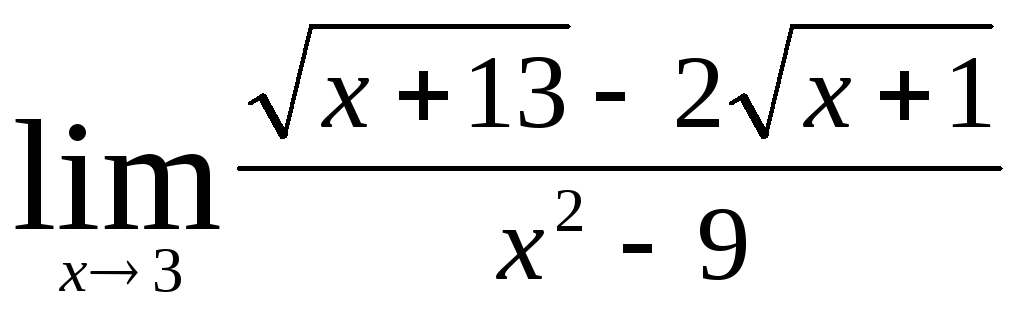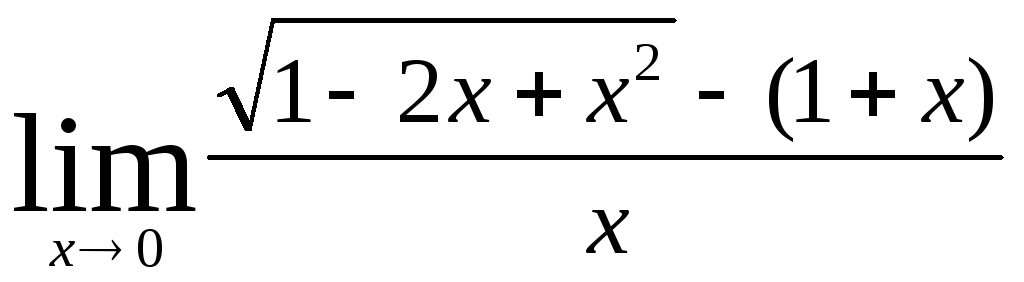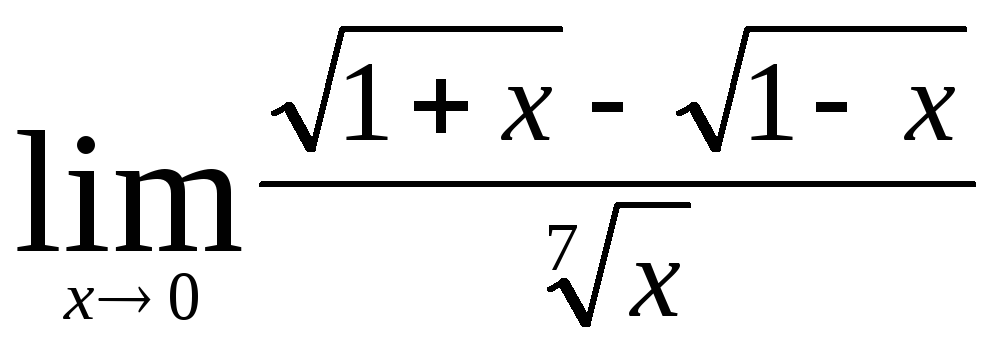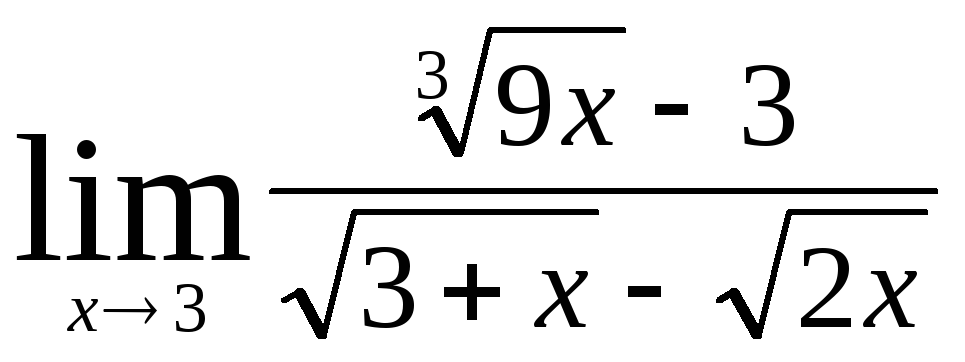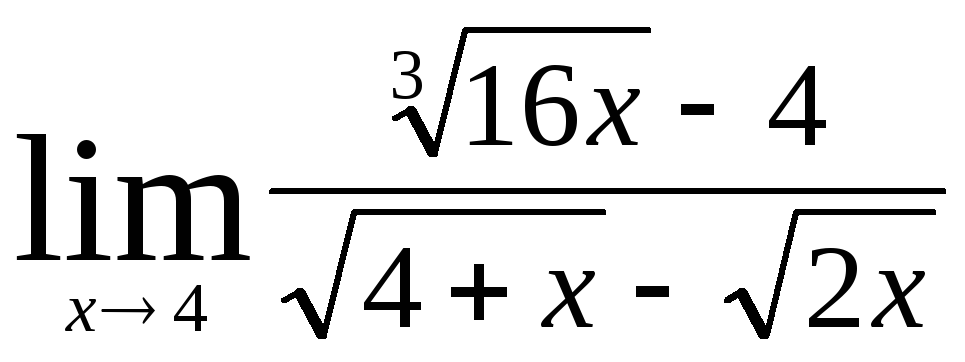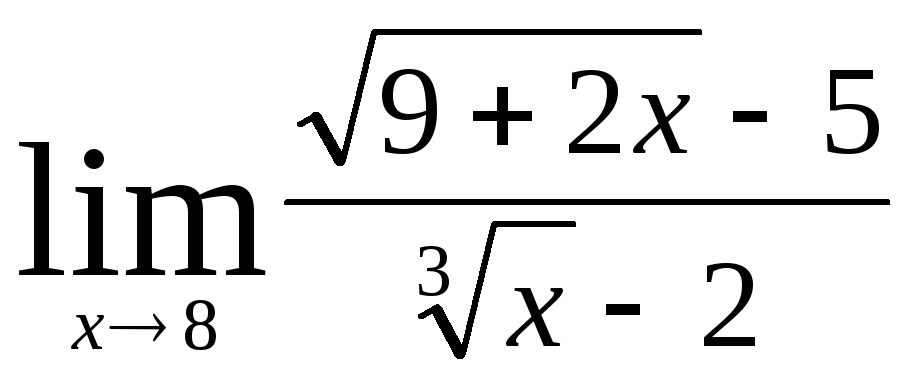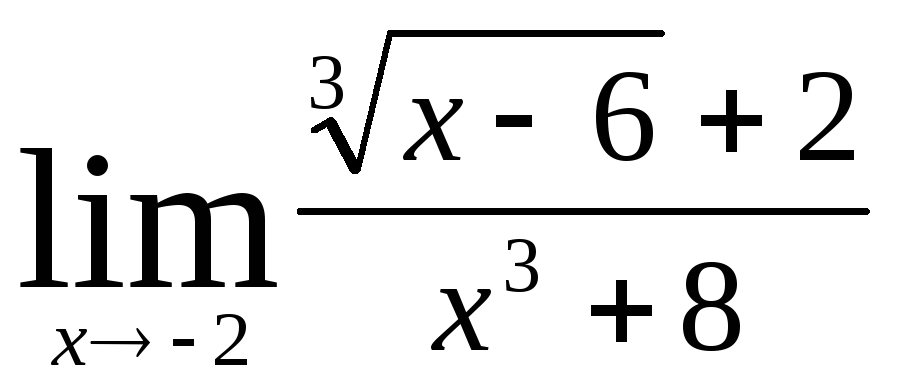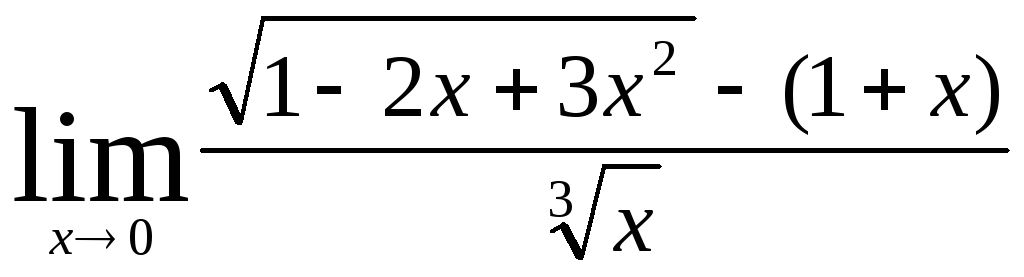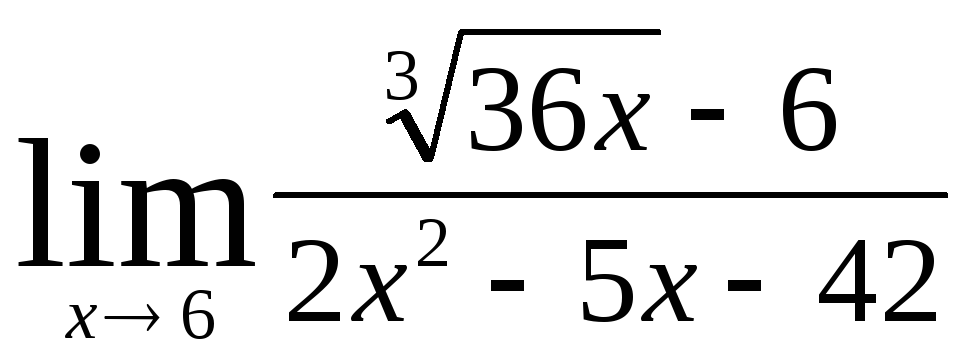Пример 4.3. Вычислить, используя первый замечательный предел:

.

Решение.

При непосредственной подстановке получаем неопределенность:

.

В данном случае для освобождения от неопределенности будем использовать первый замечательный предел . Для этого сначала домножим числитель и знаменатель дроби под знаком предела на и воспользуемся свойствами пределов (предел произведения равен произведению пределов, если эти пределы существуют):

.

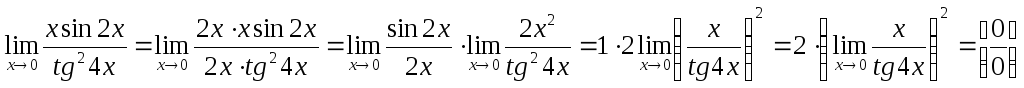Таким образом, нам не удалось избавиться от неопределенности. Воспользуемся формулами тригонометрии и еще раз применим первый замечательный предел и свойства пределов:

.

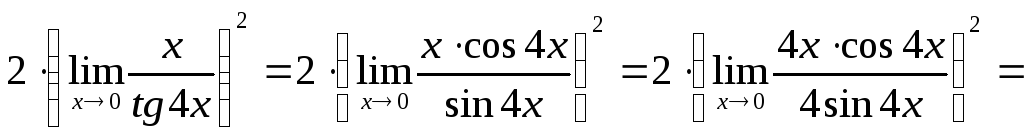
Задачи контрольной работы

В заданиях 4.3.1 – 4.3.20 найти указанные пределы, используя первый замечательный предел.

.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.

Пример 4.4. Вычислить, используя второй замечательный предел:

а) _{; б) ; в) .}

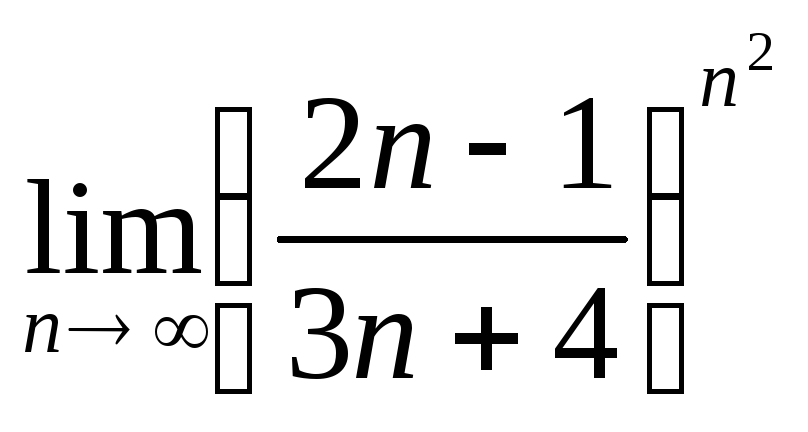Решение.

а) _.

При непосредственной подстановке получаем неопределенность:

_.

В данном случае для освобождения от неопределенности будем использовать второй замечательный предел . Для этого представим основание в виде суммы единицы и некоторой бесконечно малой величины:

.

Т.о. наш предел примет вид:

_.

_{Введем такую новую переменную , что} ,или. Припеременная_{. Показатель степени примет вид:}

.

Таким образом, пользуясь свойствами пределов и правилами действия со степенями, будем иметь:

.

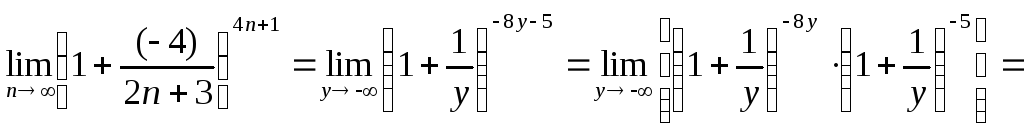
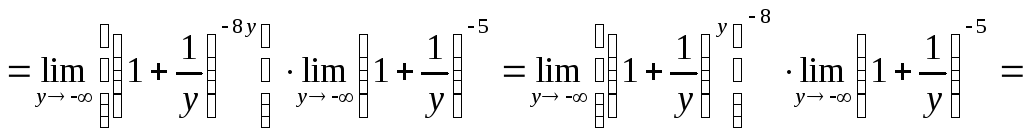
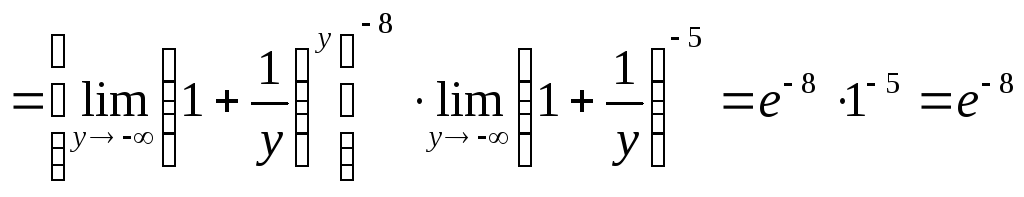б) _.

При непосредственной подстановке получаем неопределенность:

_.

В данном случае для освобождения от неопределенности будем использовать второй замечательный предел . Для этого положим, или,, тогда показатель степени примет вид: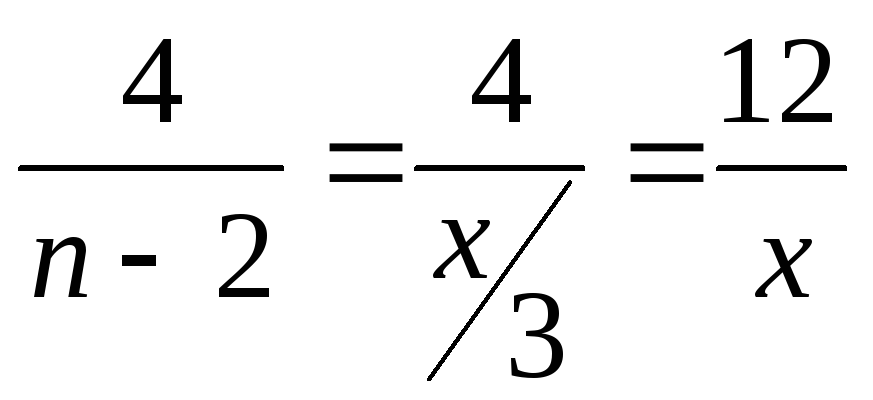. При,.

Выразив основание и показатель степени через , а также воспользовавшись свойствами пределов и правилами действия со степенями, получим

.

в) _.

При непосредственной подстановке получаем неопределенность:

_.

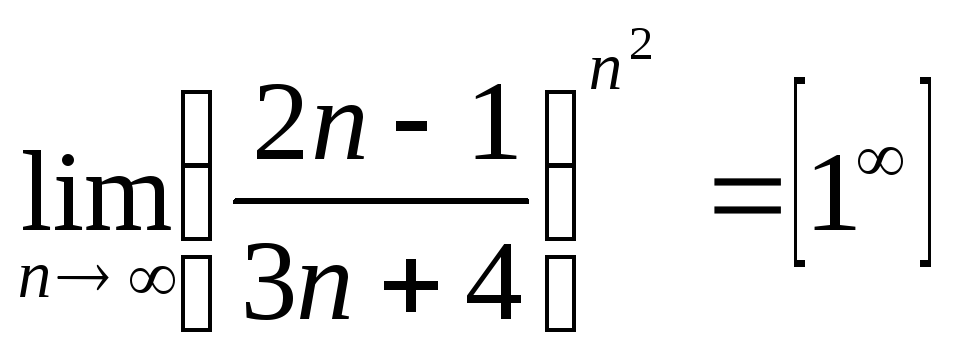В данном случае для освобождения от неопределенности будем использовать второй замечательный предел . Преобразуем выражение, стоящее в скобках. Для этого представим основание в виде суммы единицы и некоторой дроби:

.

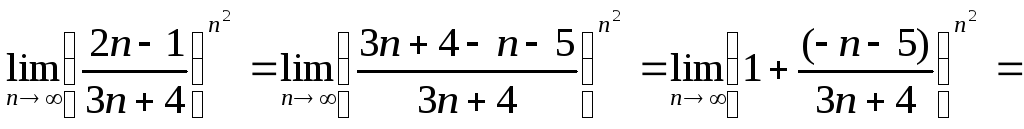
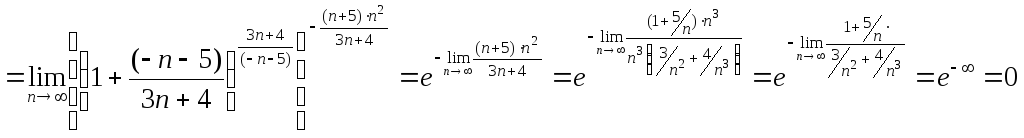Задачи контрольной работы

В заданиях 4.4.1 – 4.4.20 найти указанные пределы, используя второй замечательный предел.

.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.
.	.

5. Производные

Программные вопросы

1. Сформулируйте определение производной.

2. Каков геометрический смысл производной?

3. Что называется касательной к кривой? Напишите уравнение касательной к графику функции y = f(x).

4. Каков механический смысл первой и второй производной?

5. Каковы правила вычисления производных от суммы, произведения, частного двух функций?

6. Сформулируйте правило вычисления производной сложной функции.
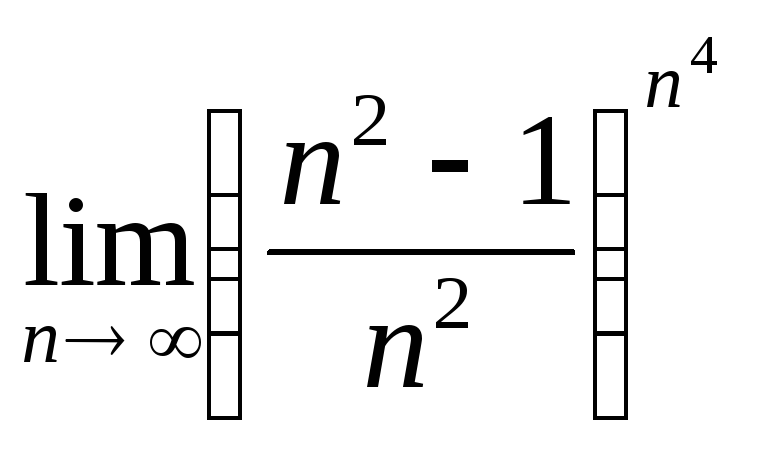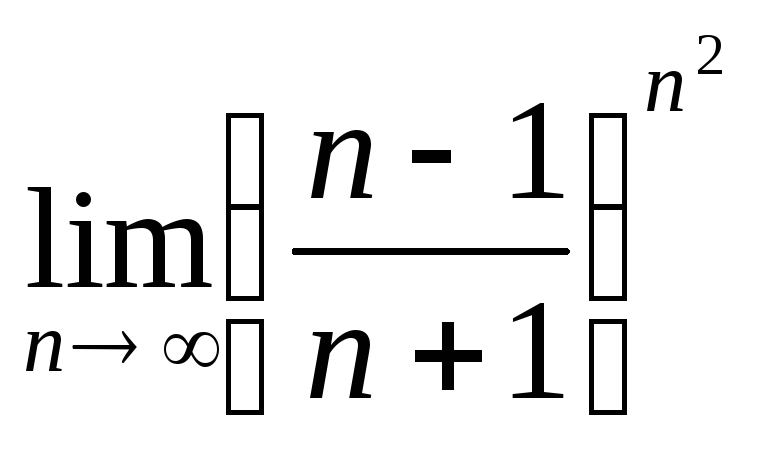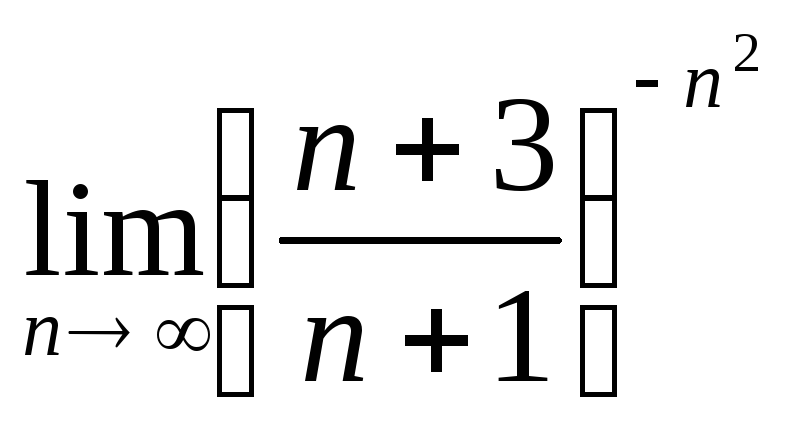