Тема II. Локальный базис криволинейной системы координат.

Пусть М х¹х²х³ – некоторая криволинейная система координат, а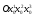– вспомогательная декартова прямоугольная система координат. Известны функции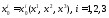, которые связывают, декартовы и криволинейные координаты, тогда локальный базис криволинейной системы координат определим как частные производные радиус-вектора точки по криволинейной координате. Мы получим тройку векторов, зависящих от выбора точки, в которой строится базис. Векторы локального базиса меняют направление и величину при переходе от одной точки к другой.

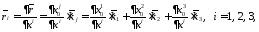
гд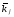е – ортонормированный базис декартовой системы координат, т.е.

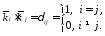
Рассмотрим различные криволинейные системы координат.

I. Полярная система координат

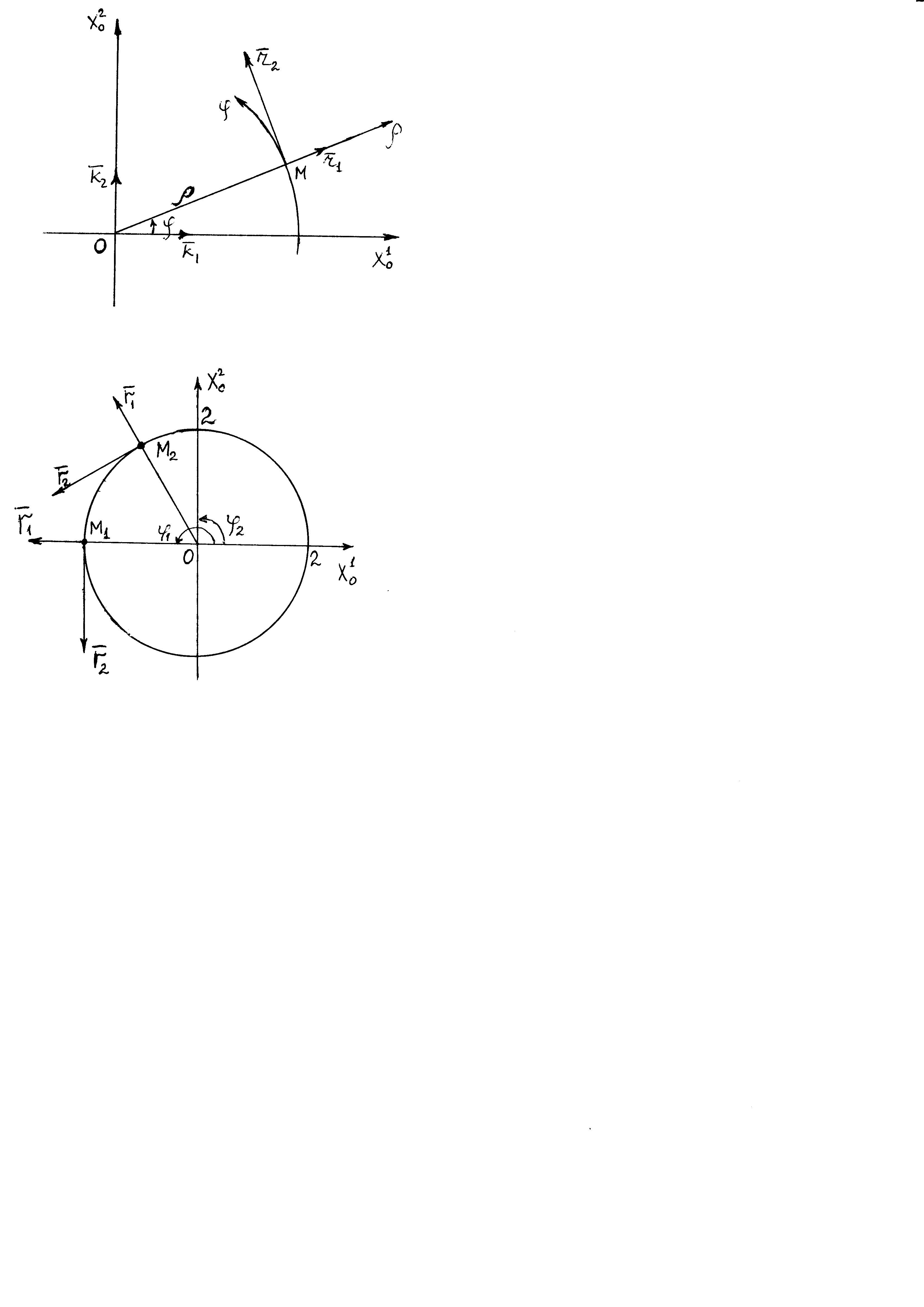
1) Введем полярные координаты:

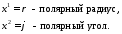
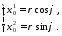
2) Определим векторы локального базиса в точке :

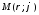Рис. 1

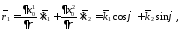
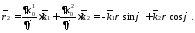
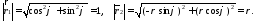
3) Построим локальный базис в точке М (рис. 1), для этого проведем через эту точку координатные линии полярной системы координат. Вдоль координатной линии изменяется только одна координата. Поэтому фиксируем каждую из координат и проводим координатную линию другой координаты. В точке М строим векторы локального базиса, которые являются касательными векторами, направленными в сторону возрастания соответствующей координаты. Длины векторов локального базиса, определяются их модулями.

Построим локальные базисы в точках М₁(2; 2π/3), М₂(2; π), рис. 2.

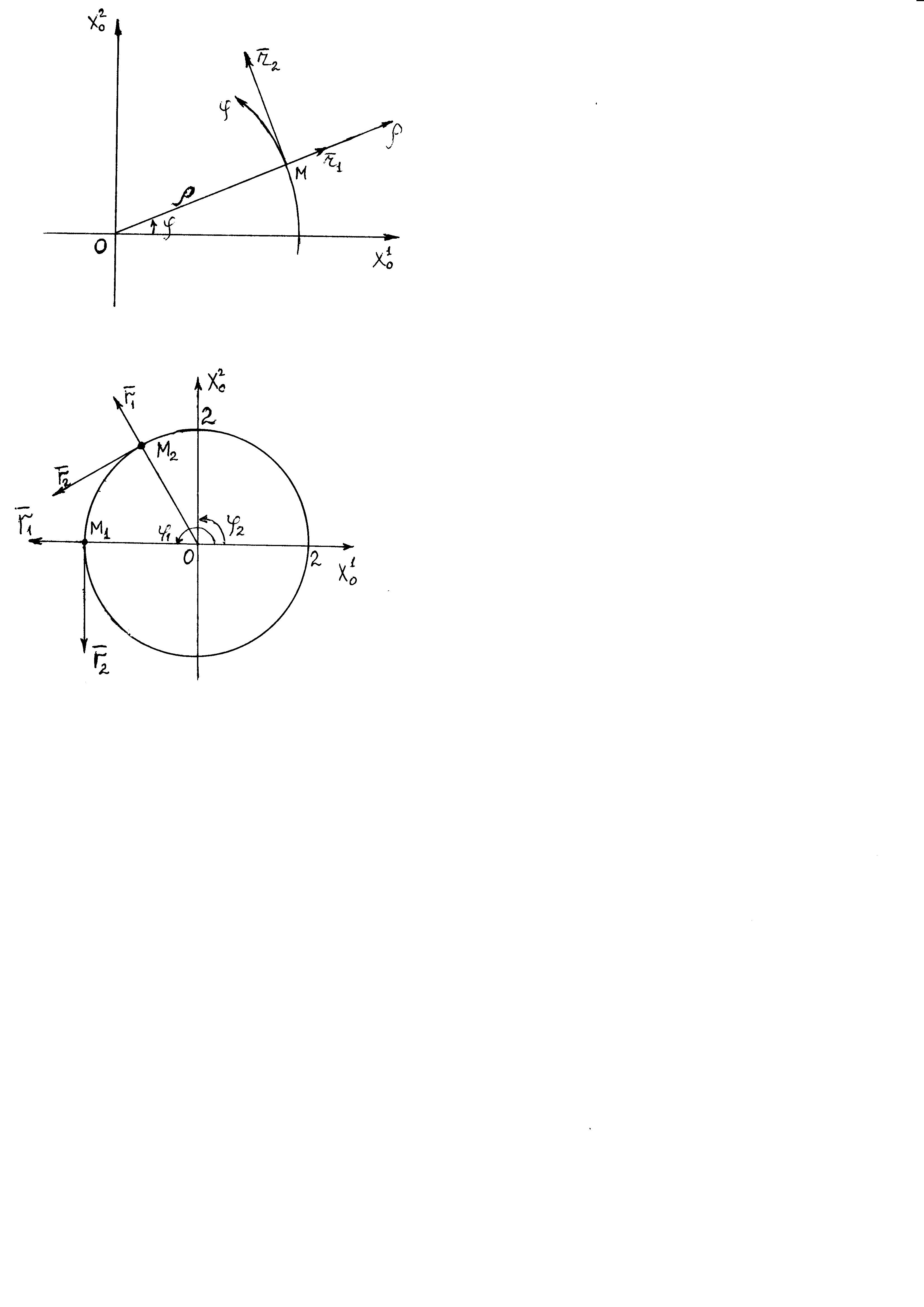
Рис. 2

II. Цилиндрическая система координат

1) Введем цилиндрические координаты: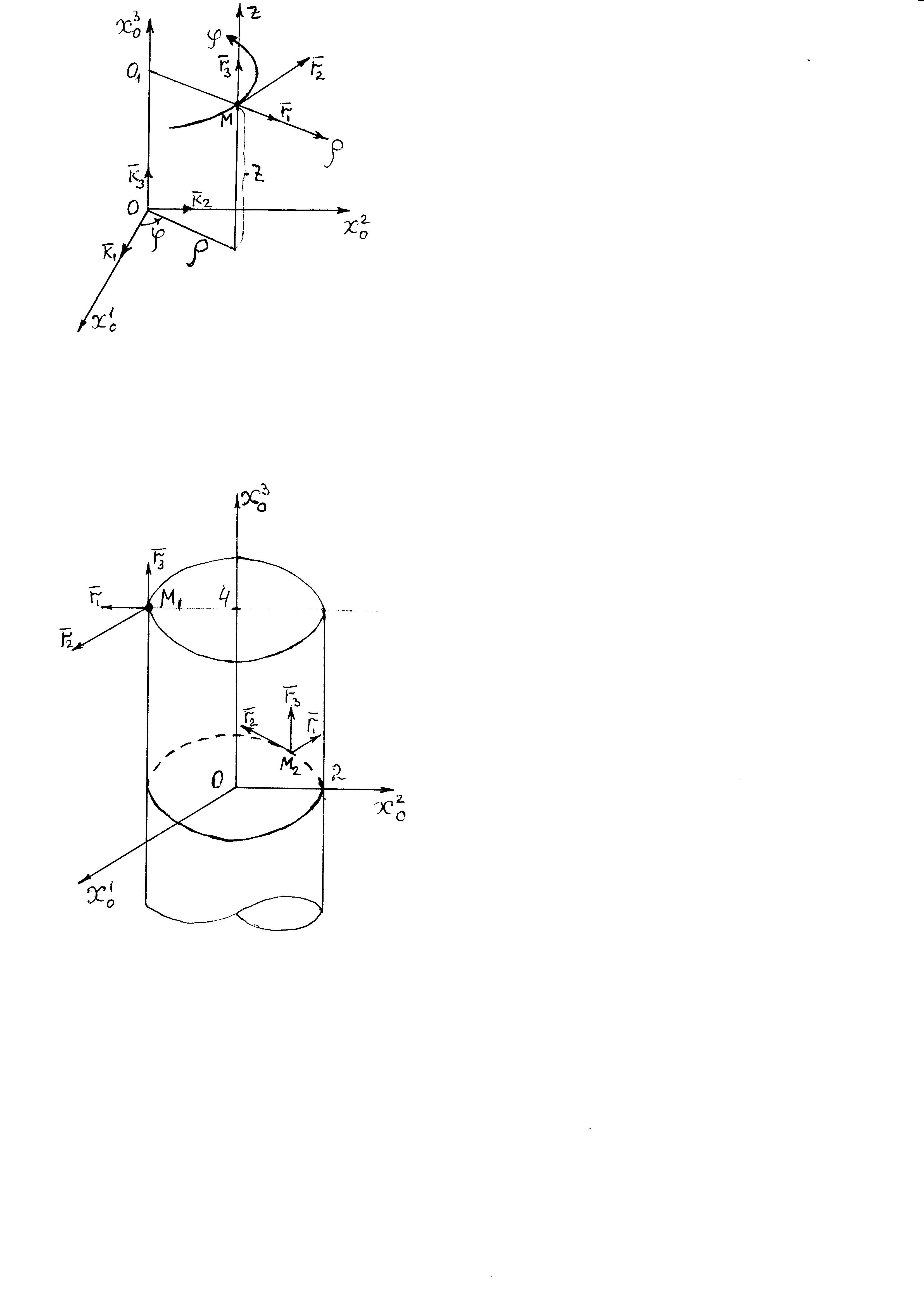

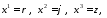
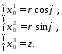
2) Определим векторы локального базиса в точке :

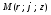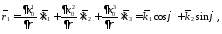
^{Рис. 3.}

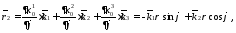
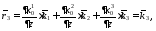
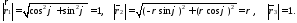
3) Построим локальный базис в точке М (Рис. 3), для этого проведем через эту точку координатные линии цилиндрической системы координат. Вдоль координатной линии изменяется только одна координата. Поэтому фиксируем две координаты и проводим координатную линию третьей координаты. В точке М строим векторы локального базиса, которые являются касательными векторами к координатным линиям. Базисные векторы направлены в сторону возрастания соответствующей координаты. Длины векторов локального базиса, определяются их модулями.

Построим локальные базисы в точках М₁(2; 3π/2; 4), М₂(2; π; 0), рис. 4.

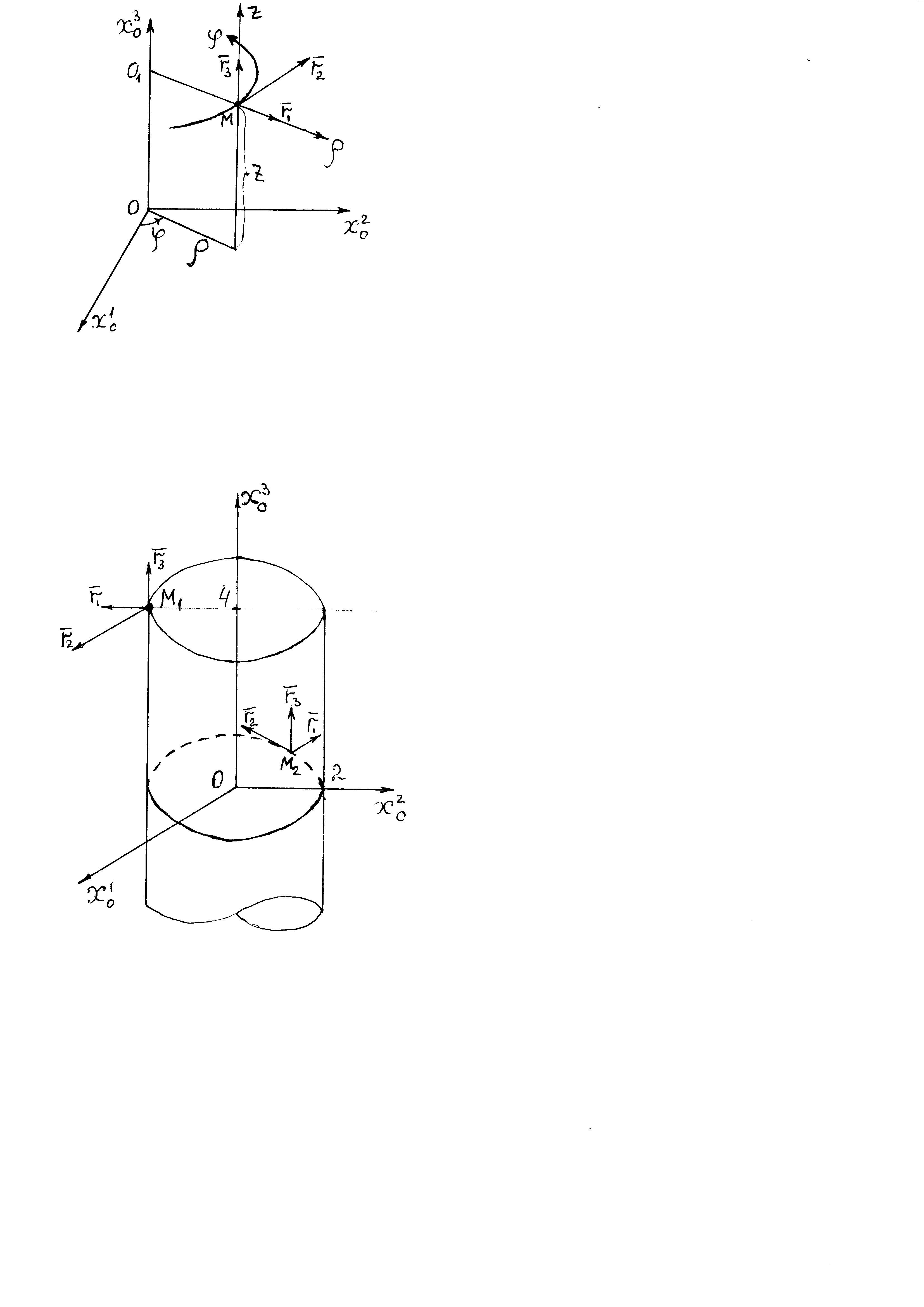
Рис. 4

III. Сферическая система координат

1) Введем сферические координаты:

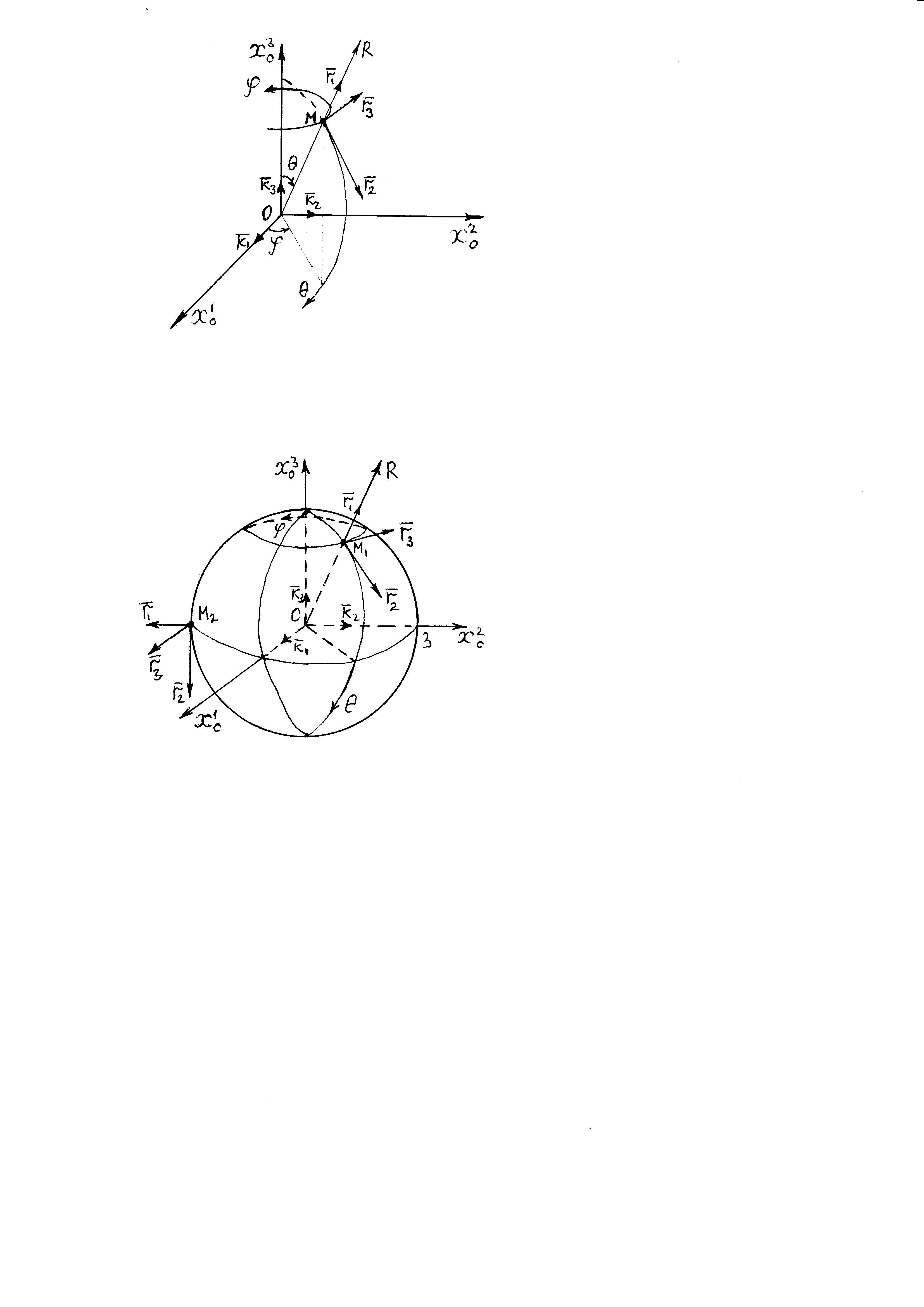
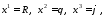
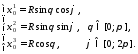
Рис. 5

2) Определим векторы локального базиса в точке :

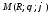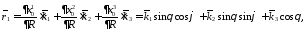
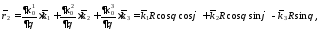
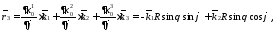
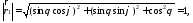
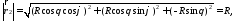
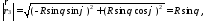
т.к.

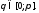
3) Построим локальный базис в точке М, для этого проведем через эту точку координатные линии сферической системы координат. Вдоль координатной линии изменяется только одна координата. Поэтому фиксируем две координаты и проводим координатную линию третьей координаты. В точке М строим векторы локального базиса, которые являются касательными векторами к координатным линиям. Базисные векторы направлены в сторону возрастания соответствующей координаты. Длины векторов локального базиса, определяются их модулями.

Построим локальные базисы в точках М₁(3; π/6; π/4), М₂(3; π/2; 3π/2). Рис. 6.

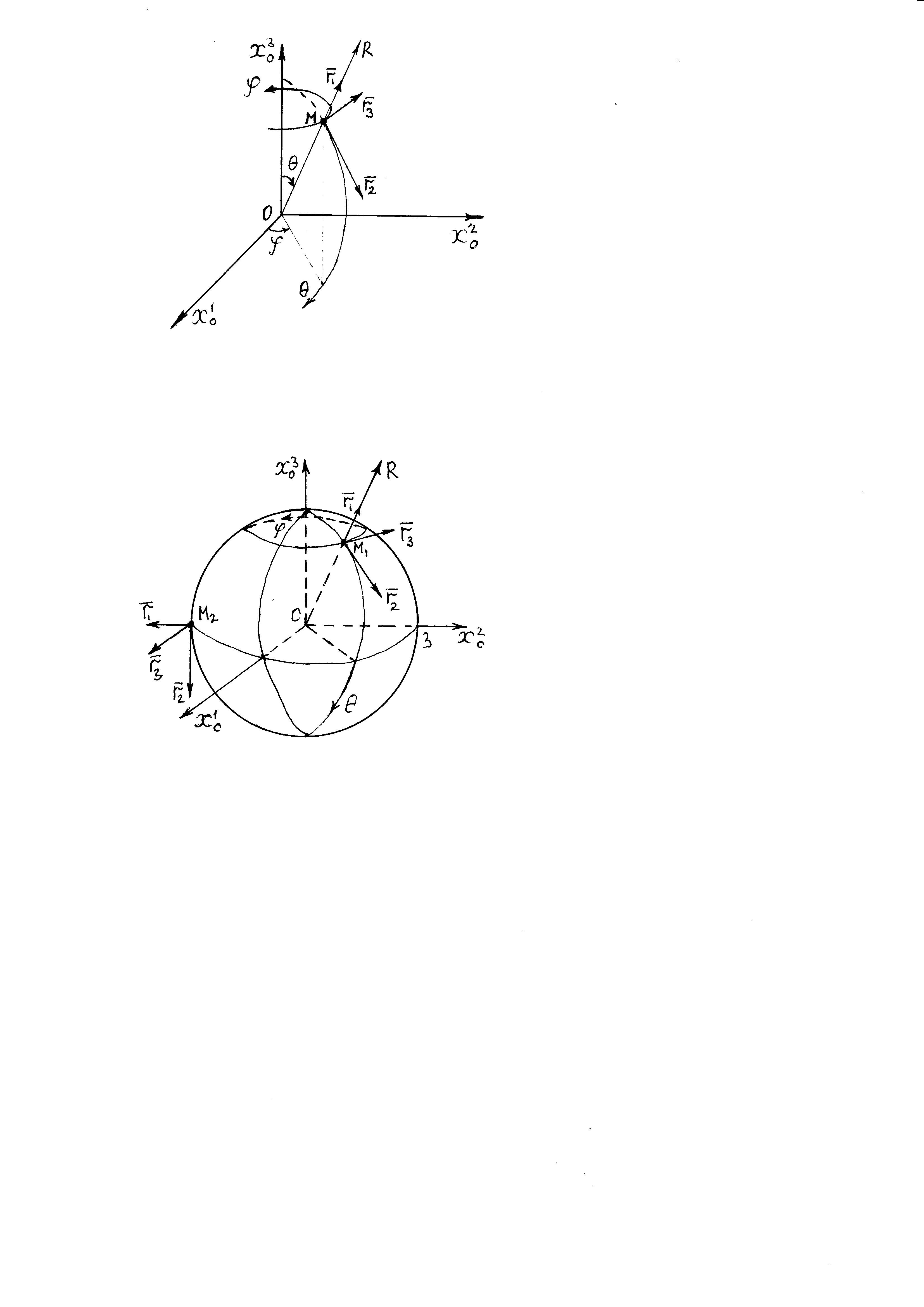
Рис. 7

IV. Тороидальная система координат.

Эту систему координат изучите самостоятельно.