
- •Министерство образования и науки Российской Федерации
- •Тема II. Локальный базис криволинейной системы координат.
- •I. Полярная система координат
- •II. Цилиндрическая система координат
- •III. Сферическая система координат
- •Тема III: Взаимный базис, ковариантные и контравариантные компоненты вектора.
- •I. Цилиндрическая система координат
- •II. Сферическая система координат
- •Тема IV. Определение тензора
- •Тема V. Операции тензорной алгебры
- •Тема VI. Элементы векторного анализа
Министерство образования и науки Российской Федерации
Челябинский государственный университет
Математический факультет
Кафедра вычислительной механики и информационных технологий
ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ
Методические указания
Челябинск 2015
Тема I. Индексные обозначения тензоров.
Развитие науки привело к необходимости введения более сложного понятия, чем скалярная величина или вектор. Новый математический объект тензор объединяет такие понятия как скаляр и вектор. Скалярная величина – это тензор нулевого ранга, вектор – это тензор первого ранга.
Индексная запись тензора – это компактная и наиболее удобная форма его записи. Сформулируем правило суммирования для индексной формы записи тензора.
Один и тот же индекс у тензора может встретиться один раз или дважды. Неповторяющийся индекс называется свободным, число свободных индексов определяет ранг тензора. Индекс, встречающийся дважды (повторяющийся индекс), является индексом суммирования, знак суммы не пишется, а подразумевается. Каждый буквенный индекс тензора может принимать значения 1, 2, … , N, где N – размерность индекса. Не теряя общности, будем в дальнейшем считать, что N=3.
Примеры записи тензоров в индексной форме:
1)
 –
тензоры нулевого ранга не имеют свободных
индексов и определяются одним числом;
–
тензоры нулевого ранга не имеют свободных
индексов и определяются одним числом;
2)
 –
тензоры первого ранга имеют один
свободный индекс, и определяются
упорядоченным набором из трех чисел
(размерность индекса равна трем);
–
тензоры первого ранга имеют один
свободный индекс, и определяются
упорядоченным набором из трех чисел
(размерность индекса равна трем);
3)
 –
тензоры второго ранга имеет два свободных
индекса, и определяются девятью числами;
–
тензоры второго ранга имеет два свободных
индекса, и определяются девятью числами;
4)
 –
тензоры третьего ранга, имеет три
свободных индекса, и определяется 27-ю
числами;
–
тензоры третьего ранга, имеет три
свободных индекса, и определяется 27-ю
числами;
5) и т.д.
Задача 1. В трехмерном евклидовом пространстве раскройте индексное выражение:



Решение. 1) Это тензор нулевого ранга, т.е. скалярная величина, ее определяет одно число:

2) Это тензор первого ранга. Один свободный индекс i определяет ранг этого тензора. Повторяющийся индекс j является индексом суммирования. Распишем тензор первого ранга как вектор:

3) Это тензор нулевого ранга, т.е. скалярная величина. Повторяющиеся индексы i и j являются индексами суммирования. Раскроем последовательно сумму сначала по индексу i, а затем по индексу j:

Задача 2. В трехмерном евклидовом пространстве раскройте индексное выражение:
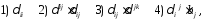
где
 – символ Кронекера.
– символ Кронекера.
Решение.  это
тензор нулевого ранга.
это
тензор нулевого ранга.
 это
тензор нулевого
ранга.
это
тензор нулевого
ранга.
 это
тензор второго ранга, состоит из 9-ти
компонент.
это
тензор второго ранга, состоит из 9-ти
компонент.
Раскрывая индексное
выражение, получим


Это тензор первого ранга, окончательно запишем результат, которым будем пользоваться в дальнейшем

Задача 3. В трехмерном евклидовом пространстве раскройте индексное выражение:


То есть имеем


Решение. 



Можно показать, что это индексная запись векторного произведения векторов в декартовой системе координат, где


Эта индексная
запись соответствует смешанному
произведению векторов:
