Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Челябинский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Матан.docx

Скачиваний:

Добавлен:

30.04.2015

Размер:

710 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Свойства неопределённого интеграла

Свойства первообразных и неопределённого интеграла вытекают из определения и соответствующих свойств производных.

1. Из определения вытекает, что

Второе равенство нужно понимать так, что производная любой из функций, составляющих неопределённый интеграл, даёт один и тот же результат, равный подынтегральной функции (это как раз и есть определение первообразной). Два написанных равенства выражают взаимную обратность операций дифференцирования и интегрирования.

2. Имеет место равенство:

где -- произвольная постоянная. Для доказательства обозначим через некоторую первообразную для , а через -- некоторую первообразную для . Тогда равенство означает, что , где -- постоянная. Это равенство верно, поскольку производные левой и правой частей дают одно и то же: , так как -- первообразная для , а , так как постоянный множитель можно вынести за знак производной и .

Итак, постоянный множитель можно вынесить за знак интеграла.

3. Интеграл от суммы равен сумме интегралов:

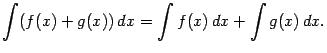
Действительно, пусть первообразная для равна , для равна , а для равна . Тогда равенство означает, что

где . Поскольку

то равенство верно; при этом мы воспользовались тем, что производная суммы равна сумме производных.

Свойства 2 и 3 называются свойствами линейности неопределённого интеграла. Из них следует, что для любых постоянных и

и, в частности,

4. Формула замены переменного. Пусть имеет смысл сложная функция , где изменяется на некотором интервале. Тогда

(1.3)

(В левой части после вычисления интеграла сделана подстановка .) Для доказательства обозначим через некоторую первообразную для и через -- первообразную для . Это означает, что и . Доказываемое равенство (1.3) эквивалентно тогда такому:

или

Для доказательства последнего соотношения достаточно проверить. что совпадают производные левой и правой частей. Но по формуле производной сложной функции получаем:

то есть то же, что и . Формула (1.3) доказана.

Заметим, что выражение в правой части (1.3) есть не что иное, как дифференциал функции . Так что мы можем записать (1.3) в виде

Теперь, после этого доказательства, мы получили право трактовать в обозначении неопределённого интеграла как некоторый дифференциал, а не просто как элемент обозначения интеграла, вроде скобки.

Линейная замена. Разберём особо случай, когда подынтегральная функция зависит от линейного выражения (где ), то есть интеграл имеет вид

В этом случае интеграл можно упростить с помощью естественной замены , откуда и . Пусть известна первообразная для :

Выполняя подстановку, получаем:

Полученную формулу

(1.4)

мы будем далее широко использовать, не всегда делая ссылки на её номер (1.4). Эту формулу следует хорошо запомнить, в особенности то, что при интегрировании с помощью линейной замены вперёд выходит множитель , а не , как при дифференцировании функции .

Например,

и т. п. При получаем

и, в частности, при

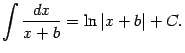
Последнюю формулу полезно рассматривать как табличную.

Замечание 1.2 При переходе от левой части к правой части в формуле интегрирования по частям происходит следующее: от функции мы переходим к функции под знаком интеграла в правой части (точнее, к дифференциалу ), то есть функцию мы дифференцируем. Одновременно от функции (или от дифференциала ) мы переходим под интегралом в правой части к , то есть функцию мы интегрируем (напомним, что первообразная для есть ).

Таким образом, применять формулу интегрирования по частям для вычисления неопределённого интеграла разумно в двух случаях:

а) либо когда функция "не слишком ухудшается" при дифференцировании, а функция "значительно улучшается" при интегрировании;

б) либо когда функция "значительно улучшается" при дифференцировании, а функция "не слишком ухудшается" при интегрировании.

Тогда дело в целом оправдано: происходит "некоторое улучшение" интеграла в правой части по сравнению с интегралом в левой части, в том смысле, что интеграл в правой части оказывается проще исходного.

В разобранном выше примере мы дифференцировали функцию , от чего она "сильно улучшилась": . Функцию мы интегрировали, отчего она "не сильно ухудшилась" (точнее говоря, совсем не изменилась, поскольку ). В результате интеграл в правой части оказался проще исходного.

Замечание 1.3 К сожалению, природа устроена так, что никакой простой формулы, позволяющей вычислить интеграл от произведения двух функций, подобно тому, как мы вычисляем производную произведения, не существует. Всё, что можно предложить по этому поводу -- это формула интегрирования по частям.

Дадим советы по наиболее часто встречающимся случаям применения этой формулы.

Если в подынтегральной функции содержатся как множители степень (где ) и синус, косинус или экспонента (показательная функция), то имеет смысл взять и дифференцировать, а к отнести синус, косинус или экспоненту, умноженные на , и интегрировать этот множитель. При этом степень при дифференцировании понизится, синус при интегрировании перейдёт в косинус, а косинус в синус (это не приведёт к сильному усложнению), экспонента же вовсе не изменится. В целом интеграл в правой части будет проще исходного.

Таким способом можно, например, вычислить интегралы , , и подобные им. Иной раз формулу интегрирования по частям приходится применять и к тому интегралу, что образовался в правой части после первого интегрирования по частям.