
- •25.Интегралы от тригонометрических функций. Универсальная тригонометрическая подстановка. Использование тригонометрических формул
- •Понижение степени подынтегральной функции
- •Метод замены переменной
- •Универсальная тригонометрическая подстановка
- •24.Интегрирование рациональных дробей
- •23.Метод неопределенных коэффициентов
- •22.Интегрирование по частям Интегрирование по частям в неопределенном интеграле
- •Интегрирование заменой переменной
- •Следствия из метода интегрирования заменой переменной
- •Первообразная и неопределенный интеграл, их свойства.
- •Экстремум функции Необходимое условие экстремума
- •Достаточное условие экстремума
- •1) Первое достаточное условие:
- •2) Второе достаточное условие
- •Дифференциал функции
- •Дифференциал функции составляет основную часть ее приращения.
- •Теоремы о дифференцируемых функциях
- •Геометрический и механический смысл производной
- •Геометрический смысл производной
- •Понятие производной Пусть задана некоторая функция . Возьмем какое-нибудь значение из области определения этой функции: . Соответствующее значение функции в этой точке будет равно .
- •Эквивалентные бесконечно малые функции. Таблица эквивалентных б.М. Функций
- •Предельные равенства для эквивалентных б.М. Функций
- •Замечательные пределы
- •Основные неопределенности пределов и их раскрытие.
- •Свойства неопределённого интеграла
- •Примеры исследования последовательностей на монотонность
- •Нестрогая монотонность
- •Основные свойства б.М. И б.Б. Последовательностей
- •Основные понятия и определения
- •Задание последовательности формулой ее общего члена
- •Рекуррентный способ задания последовательности
Замечательные пределы
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
![]()
Доказательство

Рассмотрим односторонние
пределы ![]() и
и ![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть ![]() .
Отложим этот угол на единичной окружности
(
.
Отложим этот угол на единичной окружности
(![]() ).
).
Точка K —
точка пересечения луча с окружностью,
а точка L —
с касательной к единичной окружности
в точке ![]() .
Точка H —
проекция точки K на
ось OX.
.
Точка H —
проекция точки K на
ось OX.
Очевидно, что:
![]() (1)
(1)
(где ![]() —
площадь сектора
—
площадь сектора ![]() )
)
![]()
![]()
![]()
(из ![]() :
: ![]() )
)
Подставляя в (1), получим:
![]()
Так
как при ![]() :
:
![]()
Умножаем
на ![]() :
:
![]()
Перейдём к пределу:
![]()
![]()
![]()
Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
следствия
Следствия


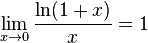

 для
для  ,
, 

Основные неопределенности пределов и их раскрытие.
Перечислим
все основные
виды неопределенностей:
ноль делить на ноль ![]() (0
на 0),
бесконечность делить на бесконечность
(0
на 0),
бесконечность делить на бесконечность ![]() ,
ноль умножить на бесконечность
,
ноль умножить на бесконечность ![]() ,
бесконечность минус бесконечность
,
бесконечность минус бесконечность ![]() ,
единица в степени бесконечность
,
единица в степени бесконечность ![]() ,
ноль в степени ноль
,
ноль в степени ноль ![]() ,
бесконечность в степени ноль
,
бесконечность в степени ноль ![]() .
.
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать неопределенности позволяет:
упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
использование замечательных пределов;
применение правила Лопиталя;
использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).
Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).
Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.

Неопределенность типа 00
Пусть заданы две функции f(x) и g(x), такие, что
limx→af(x)=0иlimx→ag(x)=0.
В этом случае говорят, что функция f(x)g(x) имеет неопределенность типа 00 в точке x=a. Чтобы найти предел при x=a, когда функция f(x)g(x) содержит неопределенность 00, нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю. Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.
Неопределенность типа ∞∞
Пусть две функции f(x) и g(x) обладают свойством
limx→af(x)=±∞иlimx→ag(x)=±∞.
где a является действительным числом, либо стремится к +∞ или −∞. Говорят, что в этом случае функция f(x)g(x) имеет в точке a неопределенность типа ∞∞. Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.
Неопределенности типа ∞−∞, 0⋅∞, ∞0, 1∞
Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа 00 и ∞∞.
1.Вычислить предел limx→1x20−1x10−1.
Решение.
Подставив напрямую значение x=1, убеждаемся, что данная функция имеет неопределенность 00 в точке x=1. Разложив числитель на множители, получаем
limx→1x20−1x10−1=[00]=limx→1(x10)2−1x10−1=limx→1(x10−1)(x10+1)x10−1=limx→1(x10+1)=110+1=2.
2.Вычислить предел limx→∞x3+3x+52x3−6x+1.
Решение.
Подстановка x→∞ показывает, что функция имеет неопределенность типа ∞∞. Разделим числитель и знаменатель на x3 (x в наивысшей степени знаменателя). В результате получаем
limx→∞x3+3x+52x3−6x+1=[∞∞]=limx→∞x3+3x+5x32x3−6x+1x3=limx→∞x3x3+3xx3+5x32x3x3−6xx3+1x3=limx→∞1+3x2+5x32−6x2+1x3=limx→∞(1+3x2+5x3)limx→∞(2−6x2+1x3)=limx→∞1+limx→∞3x2+limx→∞5x3limx→∞2−limx→∞6x2+limx→∞1x3=1+0+02−0−0=12

