Основные понятия и определения

Определение

Последовательностью называется функция, которая переводит множество натуральных чисел в некоторое множество : 

Элемент называется первым членом последовательности, - вторым, ... , - -ым или общим членом последовательности.

Пример

Задание. Для последовательности определить, чему равен третий член 

Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для заданной последовательности имеем, что 

Ответ. 

Задание последовательности формулой ее общего члена

Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Пример

Задание. Найти формулу общего члена последовательности 

Решение. Запишем каждый член последовательности в следующем виде:

Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.

Таким образом, делаем вывод, что

Ответ. Формула общего члена: 

Рекуррентный способ задания последовательности

Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член последовательности и известно, что , то есть и так далее до нужного члена.

Пример

Примером рекуррентно заданной последовательности является последовательность чисел Фибоначчи - 1, 1, 2, 3, 5, 8, 13, ... , в которой каждое последующее число, начиная с третьего, является суммой двух предыдущих: 2 = 1 + 1; 3 = 2 + 1 и так далее. Данную последовательность можно задать рекуррентно:

Интегрирование рациональных дробей

Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:

Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.

Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби: , где M(x)-многочлен, а правильная дробь.

Можно выделить несколько типов рациональных дробей:

I. Вид: .

II. Вид:(k-целое положительное число ³2).

III. Вид: .

IY. Вид:(k-целое³2).

Рассмотрим интегралы от простейших рациональных дробей.

I. .

II. =A .

III. 

=

=

+
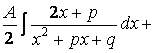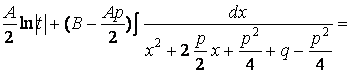