
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •1. Вычислить криволинейные интегралы:
- •2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить.
- •4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •1. Вычислить криволинейные интегралы:
- •2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить. .
- •4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •1. Вычислить криволинейные интегралы:
- •2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить.
- •4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •1. Вычислить криволинейные интегралы:
- •2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить. .
- •4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •1. Вычислить криволинейные интегралы:
- •2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить.
- •4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
- •1. Вычислить криволинейные интегралы:
- •2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить. .
- •4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
- •9. Найти производную функции u (X, y, z) в точке m по направлению , если
Вариант № 1
1. Вычислить криволинейные интегралы:
а)
![]() ,
где
,
где
![]() -
отрезок прямой, соединяющий точки
-
отрезок прямой, соединяющий точки
![]() и
и
![]() ;
;
б)
![]() ,
где
,
где
![]() -
окружность
-
окружность
![]() ;
в)
;
в)
![]() ,
где
,
где
![]() :
:
![]() от точки
от точки
![]() до
до
![]() ;
г)
;
г)
![]() ,
где
,
где
![]() :
:
![]() .
.
2. Проверить,
является ли данное выражение полным
дифференциалом функции
![]() .
Найти эту функцию. Результат проверить.
.
Найти эту функцию. Результат проверить.
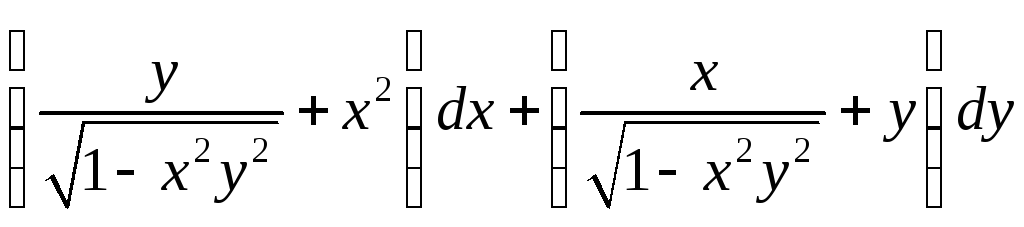
3. С помощью формулы
Грина вычислить интеграл
![]() ,
где
,
где
![]() - пробегаемый в положительном направлении
контур
- пробегаемый в положительном направлении
контур
![]() с вершинами
с вершинами
![]() .
.
4. Вычислить
поверхностный интеграл по поверхности
![]() ,
где
,
где
![]() - часть плоскости
- часть плоскости
![]() ,
отсеченная координатными плоскостями:
,
отсеченная координатными плоскостями:
![]() .
.
5. Определить координаты центра масс однородной поверхности:
![]()
6. Вычислить
поверхностный интеграл:
![]() ,
где
,
где
![]() - верхняя сторона плоскости
- верхняя сторона плоскости
![]() ,
отсеченной координатными плоскостями.
,
отсеченной координатными плоскостями.
7. Вычислить с
помощью теоремы Остроградского –
Гаусса:
![]() ,
где
,
где
![]() - внешняя сторона полной поверхности
- внешняя сторона полной поверхности
![]() .
.
8. Вычислить
интеграл, используя формулу Стокса:
![]() ,
где
,
где
![]() - эллипс
- эллипс
![]() ,
ориентированный отрицательно относительно
вектора
,
ориентированный отрицательно относительно
вектора
![]() .
.
9. Найти производную
функции u
(x,
y,
z)
в точке M
по направлению
![]() ,
если
,
если
u = x ( ln
y - arctg z ),
![]() =
8
=
8![]() +
4
+
4![]() +
8
+
8![]() ,
M(-2, 1, -1).
,
M(-2, 1, -1).
10. Вычислить поток
векторного поля
![]() (M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
(M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
![]() (M)
= 3x
(M)
= 3x![]() +
( y
+ z
)
+
( y
+ z
)![]() +
( x
- z
)
+
( x
- z
)![]() ,
(p):
x
+ 3y
+ z
= 3.
,
(p):
x
+ 3y
+ z
= 3.
11. Вычислить
циркуляцию векторного поля
![]() (M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
2x
+ y
+ 2z
= 2 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами: а) использовав определение
циркуляции; б) с помощью формулы Стокса,
если
(M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
2x
+ y
+ 2z
= 2 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами: а) использовав определение
циркуляции; б) с помощью формулы Стокса,
если
![]() (M)
= z
(M)
= z![]() +
( x
+ y
)
+
( x
+ y
)![]() +
y
+
y![]() .
.
12. Найти наибольшую
плотность циркуляции векторного поля
![]() (M)
= x
(M)
= x![]()
![]() -
xy
-
xy![]()
![]() +
z
+
z![]()
![]() в точке M
в точке M![]() (0,
1, -2).
(0,
1, -2).
13. Выяснить является
ли векторное поле
![]() (M)
= x
(M)
= x![]() y
y![]() -
2xy
-
2xy![]()
![]() +
2xyz
+
2xyz![]() соленоидальным.
соленоидальным.
Вариант № 2
1. Вычислить криволинейные интегралы:
а)
![]() ,
где
,
где
![]() -
контур треугольника с вершинами
-
контур треугольника с вершинами
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
где
,
где
![]() -
окружность
-
окружность
![]() ;
в)
;
в)
![]() ,
где
,
где
![]() - отрезок прямой от точки
- отрезок прямой от точки
![]() до
до
![]() ;
г)
;
г)
![]() ,
где
,
где
![]() :
:
![]() от точки
от точки
![]() до
до
![]() .
.
2. Проверить,
является ли данное выражение полным
дифференциалом функции
![]() .
Найти эту функцию. Результат проверить.
.
Найти эту функцию. Результат проверить.
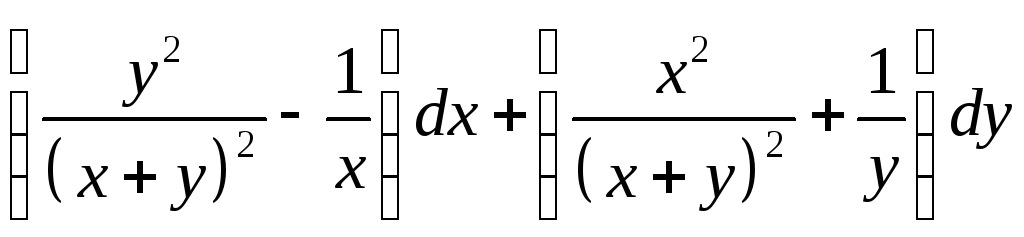 .
.
3. С помощью формулы
Грина вычислить интеграл
![]() ,
где
,
где
![]() - окружность
- окружность
![]() .
.
4. Вычислить
поверхностный интеграл по поверхности
![]() ,
где
,
где
![]() - часть плоскости
- часть плоскости
![]() ,
отсеченная координатными плоскостями:
,
отсеченная координатными плоскостями:
![]() .
.
5. Определить
координаты центра масс однородной
поверхности:
![]()
6. Вычислить
поверхностный интеграл:
![]() ,
где
,
где
![]() - внешняя сторона сферы
- внешняя сторона сферы
![]() ,
лежащая в первом октанте.
,
лежащая в первом октанте.
7. Вычислить с
помощью теоремы Остроградского –
Гаусса:
![]() ,
где
,
где
![]() - внешняя сторона поверхности тетраэдра
- внешняя сторона поверхности тетраэдра
![]() .
.
8. Вычислить
интеграл, используя формулу Стокса:
![]() ,
где
,
где
![]() - граница треугольника с вершинами в
точках
- граница треугольника с вершинами в
точках
![]() ,
,
![]() ,
,
![]() ,
ориентированная положительно относительно
вектора
,
ориентированная положительно относительно
вектора
![]() .
.
9. Найти производную
функции u
(x,
y,
z)
в точке M
по направлению
![]() ,
если
,
если
u
= ln
( 3 - x![]() )
+ xy
)
+ xy![]() z,
z,
![]() =
-
=
-![]() +
2
+
2![]() -
2
-
2![]() ,
M(1,
3, 2).
,
M(1,
3, 2).
10. Вычислить поток
векторного поля
![]() (M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
(M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
![]() (M)
= (3x
-1)
(M)
= (3x
-1)![]() +
( y
- x
+ z
)
+
( y
- x
+ z
)![]() +
4 z
+
4 z![]() ,
(p):
2x
- y
- 2z
= 2.
,
(p):
2x
- y
- 2z
= 2.
11. Вычислить
циркуляцию векторного поля
![]() (M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
3x
+ 2y
+ z
= 6 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами:
(M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
3x
+ 2y
+ z
= 6 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами:
а) использовав определение циркуляции; б) с помощью формулы Стокса, если
![]() (M)
= (x
+z)
(M)
= (x
+z)![]() +
z
+
z![]() +
(2x-y)
+
(2x-y)![]() .
.
12. Найти наибольшую
плотность циркуляции векторного поля
![]() (M)
= xy
(M)
= xy![]() +
yz
+
yz![]() +
xz
+
xz![]() в точке M
в точке M![]() (2,
0, 3).
(2,
0, 3).
13. Выяснить является
ли векторное поле
![]() (M)
= (yz
– 2x)
(M)
= (yz
– 2x)![]() +
(xz
+ zy)
+
(xz
+ zy)![]() +
xy
+
xy![]() потенциальным.
потенциальным.
Вариант № 3
1. Вычислить криволинейные интегралы:
а)
![]() ,
где
,
где
![]() -
отрезок прямой между точками
-
отрезок прямой между точками
![]() и
и
![]() ;
;
б)
![]() ,
где
,
где
![]() -
первый виток винтовой линии
-
первый виток винтовой линии
![]() ;
;
в)
![]() ,
где
,
где
![]() :
:
![]() от точки
от точки
![]() до
до
![]() ;
г)
;
г)
![]() ,
где
,
где
![]() :
:
![]() от точки
от точки
![]() до
до
![]() .
.
2. Проверить,
является ли данное выражение полным
дифференциалом функции
![]() .
Найти эту функцию. Результат проверить.
.
Найти эту функцию. Результат проверить.
![]() .
.
3. С помощью формулы
Грина вычислить интеграл
![]() ,
где
,
где
![]() - эллипс
- эллипс
![]() .
.
4. Вычислить
поверхностный интеграл по поверхности
![]() ,
где
,
где
![]() - часть плоскости
- часть плоскости
![]() ,
отсеченная координатными плоскостями:
,
отсеченная координатными плоскостями:
![]() .
.
5. Определить
координаты центра масс однородной
поверхности:
![]() .
.
6. Вычислить
поверхностный интеграл:
![]() ,
где
,
где
![]() - часть поверхности параболоида
- часть поверхности параболоида
![]() (нормальный вектор
(нормальный вектор
![]() которой образует тупой угол с ортом
которой образует тупой угол с ортом
![]() ),
вырезаемая цилиндром
),
вырезаемая цилиндром
![]() .
.
7. Вычислить с
помощью теоремы Остроградского –
Гаусса:
![]() ,
где
,
где
![]() - внутренняя сторона сферы
- внутренняя сторона сферы
![]() .
.
8. Вычислить
интеграл, используя формулу Стокса:
![]() ,
где
,
где
![]() - окружность
- окружность
![]() ,
ориентированная положительно относительно
вектора
,
ориентированная положительно относительно
вектора
![]() .
.
9. Найти производную функции u (X, y, z) в точке m по направлению , если
u
= sin(x
+2y)
+
![]() ,
,
![]() =
4
=
4![]() +
3
+
3![]() ,
M(
,
M(![]() ,
,
![]() ,
3).
,
3).
10. Вычислить поток
векторного поля
![]() (M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
(M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
![]() (M)
= x
(M)
= x![]() +
( x + z )
+
( x + z )![]() +
( y + z )
+
( y + z )![]() ,
(p): 3x + 3y + z = 3.
,
(p): 3x + 3y + z = 3.
11. Вычислить
циркуляцию векторного поля
![]() (M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
2x
+ 2y
+ z
= 2 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами:
(M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
2x
+ 2y
+ z
= 2 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами:
а) использовав определение циркуляции; б) с помощью формулы Стокса, если
![]() (M)
= (y
+ z)
(M)
= (y
+ z)![]() +
x
+
x![]() +
(y
-2z)
+
(y
-2z)![]() .
.
12. Найти наибольшую
плотность циркуляции векторного поля
![]() (M)
= xy
(M)
= xy![]()
![]() +
yz
+
yz![]()
![]() -
x
-
x![]()
![]() в точке M
в точке M![]() (1,
-2, 0).
(1,
-2, 0).
13. Выяснить является
ли векторное поле
![]() (M)
= x
(M)
= x![]() z
z![]() +
y
+
y![]()
![]() -
xz
-
xz![]()
![]() гармоническим.
гармоническим.
Вариант № 4
1. Вычислить криволинейные интегралы:
а)
![]() ,
где
,
где
![]() -
первая арка циклоиды
-
первая арка циклоиды
![]() ;
б)
;
б)
![]() ,
где
,
где
![]() -
дуга
окружности
-
дуга
окружности
![]() ;
в)
;
в)
![]() ,
где
,
где
![]() :
:
![]() от точки
от точки
![]() до
до
![]() ; г)
; г)
![]() ,
где
,
где
![]() -
контур треугольника с вершинами
-
контур треугольника с вершинами
![]() ,
,
![]() ,
,
![]() .
.
2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить.
![]() .
.
3. С помощью формулы
Грина вычислить интеграл
![]() ,
где
,
где
![]() - пробегаемый в положительном направлении
контур треугольника с вершинами в точках
- пробегаемый в положительном направлении
контур треугольника с вершинами в точках
![]() ,
,
![]() ,
,
![]() .
.
4. Вычислить поверхностный интеграл по поверхности , где - часть плоскости , отсеченная координатными плоскостями: .
5. Определить массу,
распределенную по части эллиптического
параболоида
![]() ,
с плотностью
,
с плотностью
![]() .
.
6. Вычислить
поверхностный интеграл:
![]() ,
где
,
где
![]() - часть поверхности параболоида
- часть поверхности параболоида
![]() (нормальный вектор
(нормальный вектор
![]() которой образует тупой угол с ортом
которой образует тупой угол с ортом
![]() ),
отсекаемая плоскостью
),
отсекаемая плоскостью
![]() .
.
7. Вычислить с
помощью теоремы Остроградского –
Гаусса:
![]() ,
где
,
где
![]() - сфера
- сфера
![]() .
.
8. Вычислить
интеграл, используя формулу Стокса:
![]() ,
где
,
где
![]() - окружность
- окружность
![]() ,
ориентированная положительно относительно
вектора
,
ориентированная положительно относительно
вектора
![]() .
.
9. Найти производную функции u (X, y, z) в точке m по направлению , если
u
= x![]() y
y![]() z
- ln
(z
- 1),
z
- ln
(z
- 1),
![]() =
5
=
5![]() +
6
+
6![]() +
2
+
2![]()
![]() ,
M(1,
1, 2).
,
M(1,
1, 2).
10. Вычислить поток
векторного поля
![]() (M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
(M)
через внешнюю поверхность пирамиды,
образуемую плоскостью (p)
и координатными плоскостями, двумя
способами: а) использовав определение
потока; б) с помощью формулы Остроградского
- Гаусса, если
![]() (M)
= (x + z)
(M)
= (x + z)![]() +
(z - x)
+
(z - x)![]() +
(x +2y + z )
+
(x +2y + z )![]() ,
(p): x + y + z = 2.
,
(p): x + y + z = 2.
11. Вычислить
циркуляцию векторного поля
![]() (M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
x
+ 3y
+ 2z
= 6 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами:
(M)
по контуру треугольника, полученного
в результате пересечения плоскости
(p):
x
+ 3y
+ 2z
= 6 с координатными плоскостями, при
положительном направлении обхода
относительно нормального вектора
плоскости (p)
двумя способами:
а) использовав определение циркуляции; б) с помощью формулы Стокса, если
![]() (M)
= (2y
-z)
(M)
= (2y
-z)![]() +
( x
+ 2y
)
+
( x
+ 2y
)![]() +
y
+
y![]() .
.
12. Найти наибольшую
плотность циркуляции векторного поля
![]() (M)
= xz
(M)
= xz![]() +
z
+
z![]() +
yz
+
yz![]() в точке M
в точке M![]() (3,
0, 1).
(3,
0, 1).
13. Выяснить является
ли векторное поле
![]() (M)
= (yz
- 2x)
(M)
= (yz
- 2x)![]() +
(xz
+ 2y)
+
(xz
+ 2y)![]() +
xy
+
xy![]() соленоидальным.
соленоидальным.
Вариант № 5
1. Вычислить криволинейные интегралы:
а)
![]() ,
где
,
где
![]() -
отрезок прямой от
точки
-
отрезок прямой от
точки
![]() до
до
![]() ;
б)
;
б)
![]() ,
где
,
где
![]() -
окружность
-
окружность
![]() ;
в)
;
в)
![]() ,
где
,
где
![]() -
отрезок прямой от
точки
-
отрезок прямой от
точки
![]() до
до
![]() ;
; г)
;
; г)
![]() ,
где
,
где
![]() :
:
![]() от
точки
от
точки
![]() до точки
до точки
![]() .
.
2. Проверить, является ли данное выражение полным дифференциалом функции . Найти эту функцию. Результат проверить. .
3. С помощью формулы
Грина вычислить интеграл
![]() ,
где
,
где
![]() -эллипс
-эллипс
![]() ,
пробегаемый в положительном направлении.
,
пробегаемый в положительном направлении.
