
Отчеты / Отчет13
.doc
файл:
ЛР_13_Образец_отчёта.doc
www.pds-01.boom.ru







5.7. Таблица с разрешенными кодовыми комбинациями
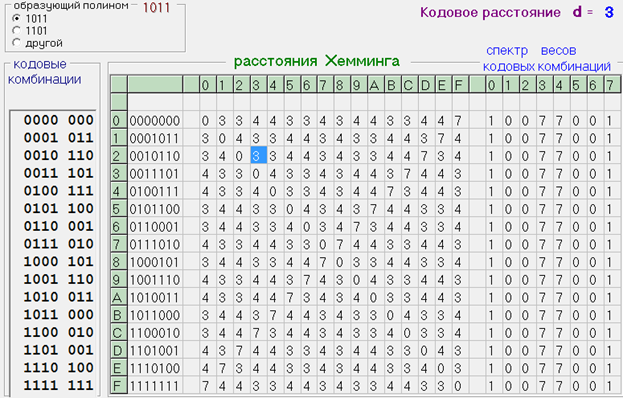
Выводы по работе:
Данная работа помогла мне в изучении основных принципов помехоустойчивого кодирования, правил построения циклических кодов и их свойств. Я исследовала обнаруживающие и исправляющие свойства циклических кодов и познакомилась с принципом построения кодирующих и декодирующих устройств циклических кодов.
Ответ на контрольные вопросы:
-
Что такое кодовое расстояние?
Кодовое расстояние d, определяемое как наименьшее расстояние Хемминга между всеми возможными парами кодовых слов, в линейном коде равно минимальному весу ненулевого кодового слова.
-
Определение и основные свойства циклического кода.
Циклическим кодом называется такой линейный код, у которого при любом циклическом сдвиге какого-либо кодового слова получается другое кодовое слово. Основное свойство: условие замкнутости по отношению к операции циклического сдвига кодовых слов.
-
Что такое расстояние Хемминга?
Расстояние Хемминга между двумя кодовыми словами равно числу единиц в сумме этих слов по модулю 2, т.е. количеству разрядов, в которых различаются эти два кодовых слова.
-
Какие векторы ошибок не могут быть обнаружены линейным циклическим кодом?
Векторы ошибок, совпадающие с кодовыми словами, не могут быть обнаружены декодером циклического кода.
-
Как связаны кратности гарантированно исправляемых кодом ошибок t и гарантированно обнаруживаемых кодом ошибок о с кодовым расстоянием d?
Кодовое расстояние d связано с кратностью t исправляемых ошибок по формуле: d>=2t+1
Кодовое расстояние d связано с кратностью o обнаруживаемых ошибок по формуле: d>=o+1
-
Как по одной известной разрешённой комбинации циклического кода определить все остальные кодовые комбинации этого кода ?
Получить все разрешённые комбинации циклического кода можно по одной известной кодовой комбинации (не нулевой). Для этого сначала надо циклически сдвинуть известную комбинацию k-1 раз. В результате получится n комбинаций. Затем сложить попарно по модулю 2 получившиеся комбинации в различных сочитаниях (по две, по три и.т.д).






