
- •Хромой Борис Петрович
- •Глава 6. Методы измерения напряжения и мощности
- •8.4.Измерение амплитудно-частотных характеристик.
- •11.2. Нормативно-правовые основы метрологии.
- •11.3. Нормативные документы по поверке и калибровке средств измерений.
- •Стандарты:
- •Инструкции.
- •11.4.Поверка средств измерений.
- •11.5. Периодическая поверка средств измерений.
- •11.10. Метрологическая аттестация средств измерений и испытательного оборудования
- •Для получения права проведения поверочных и калибровочных работ необходима метрологическая аттестация испытательного оборудования.
- •11.11.Выбор метода поверки и рабочих эталонов.
- •21. ГОСТ 12.1 – ГОСТ 12.4. Серия системы стандартов безопасности труда (ССБТ)
- •52. Вострокнутов Н.Н. Цифровые измерительные устройства. М.: издательство Эноргоатомиздат, 1990.
- •53. Хромой Б.П., Моисеев Ю.Г. Электрорадиоизмерения: учебник для техникумов,М.: издательство Радио и связь,1985.
- •54. Блюдин Е.К. и др. Портативные осциллографы. М.:издательство Сов. радио,1978.

1
Хромой Борис Петрович
Метрология и измерения в телекоммуникационных системах (Том.1).
Рассматриваются вопросы метрологии, методов и средств измерений параметров и электрических цепей, применяющихся в технике связи. Основное внимание уделено методам и средствам относящимся к общим измерениям.
В дальнейшем предполагается издание второго тома, содержание которого будет направлено на специальные измерения, применяющиеся в аналоговых и цифровых телекоммуникационных системах.
Книга рассчитана на специалистов отрасли «связь», работающих с широким ассортиментом средств измерений при строительстве, эксплуатации и ремонте оборудования, поверителей средств измерений.
Книга может использоваться как учебное пособие студентами, изучающими курсы; «Метрология стандартизация и сертификация» (специальности 07170001, 07190001, 2090006ДО, 20110001, 20120002, 20180001, 22040001); «Метрология и радиоизмерения» (специальности 07150001, 20070001); «Метрологическое обеспечение телекоммуникационных систем» (специальности 201000, 071700);«Метрологическое обеспечение технической эксплуатации телекоммуникационных систем» (специальность 2010001).
2
ПРЕДИСЛОВИЕ
На протяжении всего XX столетия потребности техники связи служило мощным стимулом развития методов и средств измерения электрических величин или, как их обычно называют - «электрических» измерений. Первоначально, еще в конце XIX века в массовом порядке измерялись лишь постоянные электрические величины. Когда электроэнергетика перешла на переменный ток, электроизмерения поднялись на уровень промышленной частоты. Расширялся и «ассортимент» измеряемых физических величин их диапазон. Так применение синусоидального тока в энергетике привел к необходимости конструирования трансформаторов, электродвигателей и различных исполнительных устройств, работающих на переменном токе, а следовательно, измерение индуктивностей, емкостей, переменных токов и напряжений.
Появление проводной связи, основанной на использовании азбуки Морзе, первоначально не вызвало появления новых измерительных задач, однако когда были проложены трансатлантические кабели и стало очевидным целесообразность увеличения эффективности их использования путем увеличения скорости передачи, появились проблема конструирования более совершенных кабелей и измерения коэффициента отражения, параметров согласования входа и выхода, комплексных сопротивлений и распределенных параметров L, R, С. Далее нарастание «потребностей» техники связи происходило стремительными темпами, особенно с развитием радиосвязи. Напомню молодым читателям, что еще до второй мировой войны, в 1935-37 годах, промышленность ряда стран выпускала радиоприемники, устанавливаемые в автомобилях. Уже в эти годы издавались книги, объемом более 500 страниц, специально посвященные измерениям в автомобильных радиоприемниках. «Электроизмерения», теперь стали именоваться «электрорадиоизмерениями».
Дальнейшее развитие связи шло в направлении освоения все новых более высоких частотных диапазонов. Использование диапазона УКВ привело к распространению новых видов модуляции, требующих большой полосы частот для организации радиоканала, например частотной модуляции. Появилась необходимость в измерении параметров новых видов модуляции и соответствующих средств измерений. Промышленность, удовлетворяя задачам телевизионной техники, спутниковых и радиорелейных линий осваивала выпуск средств измерения новых типов в частотном диапазоне вплоть до верхней границы СВЧ. Параллельно развивались системы проводной многоканальной связи с частотным уплотнением. Специфика этих систем такова, что для их настройки в процессе строительства и эксплуатации появились не только специализированные средства измерения, но и новая терминология, относящаяся к нормируемым и измеряемым
3
параметрам.
Появление современных цифровых систем передачи организованных как обычным электрическим, так и по волоконно-оптическим кабелям, атак же систем подвижной связи вызвало новую волну научных и промышленных проблем в развитии средств измерений, или как теперь принято говорить, «метрологического обеспечения». В обиход вошли новые типы параметров, такие как «джиттер» или «вандер», для которых не всегда удобно подходят отечественные термины. Появилисьи необходимые для их измерения приборы.
С появление цифровых систем связи появились и новые измерительные задачи, вообще говоря, не относящиеся к физическим величинам. Так, например, измеритель коэффициента ошибок, предназначенный для измерения отношения ошибочно принятых к символов к объему числу символов, принятых за определенный интервал времени не является физической величиной (нет такого эталона), однако данный параметр является одним из определяющих качество функционирования цифровой системы передачи. К подобным средствам измерений следует отнести многочисленные так называемые «анализаторы протоколов», предназначенные для контроля за правильностью функционирования аппаратуры при пакетной передаче информации, систем сигнализации ит.п.
Расширилась номенклатура и традиционных типов средств измерений, так например, семейство генераторов измерительных сигналов пополнилось генератором псевдослучайных последовательностей, семейство различных анализаторов пополнилось анализатором логических состояний и др.
Многолетняя педагогическая практика автора данной книги в МТУСИ, показала, что изучение метрологических аспектов современной техники связи методически целесообразно разбить на два последовательных этапа. На первом этапе изучаются основы метрологии и общих измерительных задач, на втором этапе изучаются особенности специальных измерений, относящихся к современным телекоммуникационным системам. Здесь должна соблюдаться та же последовательность, что и при изучении литературы: вначале изучается алфавит, части речи и грамматика, а затем читаются книги, или в музыке - вначале изучаются гаммы, нотная грамота, а затем музыкальные произведения. Однако, в отличие от приведенных выше примеров при изучении измерительных техники связи дело не только в том, что читателю предлагается идти от простого к сложному. Многие вопросы, такие как теоретические основы метрологии, никак нельзя отнести к простым. Дело в том, что параллельно переходу к цифровым методам передачи, осуществлялся переход к конструированию средств измерений на основе цифровых методах обработки информации. Было бы неправильным считать, что цифровые приборы
4
существенно, или вообще сложнее аналоговых. Достаточно изучить принципы дискретизации, квантования и кодирования, общие для всех цифровых измерительных приборов, и читатель легко разберется как работает цифровой измеритель временных интервалов, частотомер или вольтметр, однако при условии, если он уже знает об их аналоговых эквивалентах. Например, для такого, что бы разобраться как действует уравновешенный мост в цифровом приборе, целесообразно вообще иметь знания о свойствах мостовых схем. Тем не менее, цифровые измерительные приборы общего назначения сравнительно легко изучаются, поскольку значительная часть их разрабатывалась и выпускалась в советское время и их принцип действия, а иногда и полные принципиальные схемы прикладывались в виде описания к самому прибору. Иначе обстоит дело в настоящее время. Современный рынок измерительной техники весьма насыщен и в условия жесткой конкуренции, фирмы ограничиваются лишь той документацией, которая позволяет грамотно эксплуатировать прибор, но в качестве «черного ящика». Структура прибора, устройство его частей, алгоритмы работы, а тем более программное обеспечение, являются секретами фирмы. Именно по этой причине, в большинстве книг, в которых рассматриваются вопросы измерений в телекоммуникационных системах, измерительные приборы представляются ящиком с двумя проводами, соединенными со стойкой аппаратуры и изображается пользовательский интерфейс на экране дисплея. Измерительные задачи, если они изучаются сразу с цифровых телекоммуникационных систем, зачастую остаются не понятыми.
Публикуемая книга рассчитана на широкий круг читателей: инженеров, занимающихся эксплуатацией оборудования и измерительной техники, поверителей средств измерений, учащихся.
Автор.
6
Глава 1. Предмет и задачи метрологии.
1.1. Основные термины, применяемые в метрологии.
Термин метрология (англ.- metrology) произошел от греческих слов: μετρον-
мера и λογοζ- учение, слово. В современном понимании – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
К основным направлениям метрологии относятся: общая теория измерений; единицы физических величин и их системы; методы и средства измерений; методы определения точности измерений, основы обеспечения единства измерений; эталоны и образцовые средства измерений; методы передачи размеров единиц от эталонов рабочим средствам измерений. Часть задач, решаемых метрологией, носит научный характер. Раздел метрологии, предметом которого является разработка фундаментальных основ метрологии называется теоретической метрологией. Иногда применяют термин фундаментальная метрология.
Раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимой точности измерений в интересах общества, называется законодательной метрологией (англ.- en legal metrology).
Раздел метрологии, предметом которого являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии называется практической (прикладной) метрологией.
К практическим задачам метрологии относятся производство и выпуск в обращение рабочих средств измерений, обеспечивающих определение с требуемой точностью характеристик продукции, государственные испытания средств измерений, ведомственные поверки средств измерений, ревизии состояния измерений на предприятиях и организациях.
Термины и определения основных понятий метрологии необходимы для понимания книги. Определение отдельных терминов будет даваться по мере необходимости, однако ряд терминов необходимо освоить на первых этапах изучения метрологии. Более подробно со стандартизированными терминами можно ознакомиться в документе РМГ29-99 [1].
7
Измерение (англ.- measurement) – процесс нахождения значения физического величины опытным путем с помощью специальных технических средств.
Единство измерений (англ.- informity of measurements, traceability)– состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны с заданной вероятностью и не выходят за установленные пределы.
Погрешность измерения (англ.- en error of a measurement) – отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Точность измерений (англ.- en accuracy of a measurement) одна из характеристик качества измерений, отражающая близость их результатов к нулю погрешности результата измерения.
Средство измерения (англ.- en measuring instrument) – техническое средство,
предназначенное для измерений, имеющее нормированные метрологические характеристики воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени. По техническому назначению средства измерений подразделяются на меры, измерительные приборы, измерительные преобразователи, вспомогательные средства измерений, измерительные установки и измерительные системы.
Мера (англ.- en material measure) - средство измерений, предназначенное для воспроизведения и\или хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.
Различают следующие разновидности мер:
однозначная мера – мера, воспроизводящая физическую величину одного размера (например, гиря 1 кг);
многозначная мера - мера, воспроизводящая ряд воспроизводящая физическую величину разного размера;
набор мер - комплект мер разного размера одной и той же физической величины, предназначенных для применения на практике как в отдельности, так и в различных сочетаниях;
8
магазин мер - набор мер, конструктивно объединенных в единое устройство, в котором имеются приспособления для их соединения в различных комбинациях.
Измерительный прибор (англ.- en measuring instrument) - средство измерений,
предназначенное для получения значения измеряемой физической величины в установленном диапазоне. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно и их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называют показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.
Измерительная установка (англ.- en measuring installation) –cовокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей и других устройств, предназначенная для измерений одной или нескольких физических величин и расположенных в одном месте.
Измерительная система (англ.- en measuring system) –cовокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей и других технических средств, размещенных в разных точках контролируемого объекта и т.п. с целью измерений одной или нескольких физических величин, свойственных этому объекту, и выработки измерительных сигналов в разных целях.
Измерительно-вычислительный комплекс - функционально объединенная cовокупность средств измерений, ЭВМ и вспомогательных устройств, предназначенная для выполнения в составе измерительной системы конкретной измерительной задачи.
Измерительный преобразователь (англ.- en measuring transducer) – техническое средство с нормативными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или печати.
По характеру преобразования различают аналоговые, аналого-цифровые, цифроаналоговые преобразователи. По месту в измерительной цепи различают первичные и промежуточные преобразователи. Первичный преобразователь - измерительный преобразователь, на который непосредственно воздействует измеряемая физическая величина, т.е. первый преобразователь в измерительной цепи измерительного прибора (установки, системы). Масштабный преобразователь служит для изменения измеряемой физической величины в заданное число раз.
9
Вспомогательное средство измерений (англ.-auxiliary measuring instrument) -
средство той физической величины, влияние которой на основное средство измерений или объект измерений необходимо учитывать для получения результатов измерений требуемой точности.
1.2.Классификация измерений.
Принято различать несколько видов измерений. Их классификация осуществляется на основе характера зависимости измеряемой величины от времени, условий, определяющих погрешность результата измерений, и способов выражения результатов.
По характеру зависимости измеряемой величины от времени измерения делятся, на статические и динамические. Статические измерения соответствуют случаю, когда измеряемая величина остается постоянной, динамические, когда измеряемая величина изменяется.
По способам получения результатов различают прямые, косвенные, совокупные и совместные измерения.
Прямым методом измерений называют метод, искомое значение величины получают непосредственно. В качестве примера можно привести измерение напряжения вольтметром.
Косвенным методом измерений – называют метод, при котором искомое значение физической величины определяют на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или сложно измерить непосредственно. Например, затухание, вносимое четырехполюсником, обычно вычисляют по измеренным значениям входного и выходного напряжений.
Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых и искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. Например, значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнения) масс различных сочетаний гирь. Для определения значения исходных величин число уравнений должно быть не меньше числа величин.
10
Совместные измерения - производимые одновременно измерения двух или нескольких неодноименных величин для нахождения функциональной связи между ними. Например, сопротивление измерительного резистора при температуре 20оС и температурные коэффициенты сопротивления, находят по результатам прямых измерений его сопротивления при различных температурах.
По способу выражения результатов измерений принято различать абсолютные и относительные измерения. Абсолютное измерение основано на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Примером абсолютного измерения является измерение силы тока в амперах. Относительным называют измерение отношения величины к одноименной величине, играющей роль единицы, или изменения величины по отношению к одноименной величине, принимаемой за исходную. Примером относительного измерения является измерение коэффициента отражения в линии.
Измерения классифицируются также по используемому методу измерения- совокупности приемов использования принципов и средств измерений. Различают следующие методы измерений.
Метод непосредственной оценки, в котором значение величины определяют непосредственно по показывающему средству измерения.
Метод сравнения с мерой, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
Этот метод имеет следующие модификации: нулевой метод, метод замещения,
метод дополнения, дифференциальный метод.
Нулевой метод - метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
Метод замещения - метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
Метод дополнения - метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
Дифференциальный метод – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.
1.3. Основные характеристики измерений.
11
Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность измерений.
Принцип измерений - физическое явление или эффект, положенное в основу измерений. Например, измерение мощности с использованием термоэлектрического эффекта.
Погрешность измерений - отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Истинное значение физической величины – значение, которое идеальным образом отражает свойства объекта в качественном и количественном отношениях. Истинное значение неизвестно (иначе не было бы смысла проводить измерения), и по этой причине в метрологии используют так называемое действительное значение, которое приближается к нему в степени достаточной для практических целей.
Точность измерения – качество измерения, отражающее близость к нулю погрешности результата измерения. Считают, что чем меньше погрешность измерения, тем выше его точность.
Правильность измерений - качество измерений, отражающее близость к нулю систематических погрешностей (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит от того технического состояния, в котором находились средства измерений при проведении эксперимента.
Достоверность измерения - степень доверия к результатам измерений. Измерения, для которых известны вероятностные характеристики отклонения результатов от истинного значения, относятся к категории достоверных.
Сходимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполненных в одинаковых условиях.
Воспроизводимость измерений - качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в различное время, в различных местах).
1.4. Физические величины и единицы.
Согласно РМГ29-99 «Рекомендации по межгосударственной стандартизации ГСИ. Метрология. Основные термины и определения» [1] под физической величиной понимается: « Одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в

12
количественном отношении индивидуальное для каждого из них». Индивидуальность в количественном отношении следует понимать в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого.
Развитие науки и техники, рост научно-технических и экономических связей привели к необходимости установления единообразия единиц измерений в международном масштабе. Требовалась единая система единиц физических величин, практически удобная и охватывающая различные области измерений. Международный комитет по мерам и весам выделил из своего состава комиссию по разработке единой Международной системы единиц. Этой комиссией был разработан проект Международный системы единиц, который был утвержден XI Генеральной конференцией по мерам и весам. Принятая система была названа Международной системой единиц, сокращенно СИ (SI — начальные буквы французского наименования
Sуstéme Inernаtiоnаl).
В РФ действует ГОСТ 8.417—81 ГСИ «Единицы физических величин». Наиболее употребительные в электрорадиоизмерениях единицы приведены в табл. 1.1.
Таблица 1.1
Величина |
|
|
Единица |
|
|
|
|
|
|
Наименование |
Размерность |
Наименование |
Обозначение |
|
|
|
|
Международное |
|
|
|
|
Русское |
|
|
|
|
J |
|
Энергия, работа, |
L2 MT-2 |
джоуль |
Дж |
|
количество теплоты |
|
|
W |
|
Мощность, поток |
L2 MT-3 |
ватт |
Вт |
|
энергии |
|
|
C |
|
Количество |
TI |
кулон |
Кл |
|
электричества |
|
|
|
|
(электрический заряд) |
|
|
V |
|
Электрическое |
L2 MT-3I-1 |
вольт |
В |
|
напряжение, |
|
|
|
|
электрический |
|
|
|
|
потенциал, разность |
|
|
|
|
электрических |
|
|
|
|
потенциалов, |
|
|
|
|
электродвижущая сила |
|
|
F |
|
Электрическая емкость |
L-2M-1T4I2 |
фарад |
Ф |
|
Электрическое |
L2MT-3I-2 |
ом |
Ω |
Ом |
сопротивление |
|
|
S |
|
Электрическая |
L-2M-1T3I2 |
сименс |
См |
|
проводимость |
|
|
H |
|
Индуктивность, |
L2MT-2I-2 |
генри |
Гн |
|
взаимная |
|
|
|
|
индуктивность |
|
|
Т |
|
Плотность магнитного |
МТ-2I-1 |
тесла |
Тл |
|

13
потока, магнитная |
|
|
|
|
индукция |
|
|
Wb |
|
Поток магнитной |
L2MT-2I-1 |
вебер |
Вб |
|
индукции, магнитный |
|
|
|
|
поток |
|
|
Hz |
|
Частота |
Т-1 |
герц |
Гц |
|
Сила электрического |
I |
ампер |
А |
А |
тока |
|
|
|
|
При разработке системы СИ специалисты исходили из того, чтобы охватить системой все области науки и техники; принять удобные для практики размеры основных единиц, уже получивших распространение; выбрать в качестве основных единицы таких величин, воспроизведение которых возможно с наибольшей точностью. В системе СИ в качестве основных единиц приняты: метр - единица длины, килограмм
-единица массы, кельвин - единица температуры, кандела - единица силы света, ампер
-единица силы тока, секунда - единица времени, моль - количество вещества. Остальные единицы являются производными.
Для выражения результатов измерений в узаконенных единицах размер последних должен либо храниться или воспроизводиться на месте, либо передаваться каким-то образом с места хранения или воспроизведения. В зависимости от этого различают централизованное и децентрализованное воспроизведение единиц физических величин. В первом случае оно осуществляется с помощью специальных технических средств, называемых эталонами, а для передачи размера единиц используются образцовые средства измерений. Во втором случае единица производной физической величины (например, площади) воспроизводится на месте через единицы основных физических величин. Последние, хранятся и воспроизводятся только централизованно в соответствии с их определением.
Главной задачей современной метрологии является создание полной системы взаимосвязанных естественных эталонов на основе использования фундаментальных физических констант и высокостабильных квантовых явлений. Важный шаг в решении этой задачи сделан XVII Генеральной конференцией по мерам и весам, принявшей в 1983 г. новое определение метра - как длины пути, проходимого светом в вакууме за промежуток времени, равный 1/299792458 с. При таком подходе единица длины может воспроизводиться децентрализованно, с помощью фундаментальной физической константы - скорости света - и единицы времени-секунды, определяемой через период эталонной частоты, передаваемой по радио. Единица времени, и частоты воспроизводятся сейчас с наименьшей погрешностью.
14
1.5. Эталоны и образцовые средства измерений.
Чтобы обеспечить единство измерений, необходима тождественность единиц, в которых проградуированы все средства измерений одной и той же физической величины. Для этого применяют средства измерений, хранящие и воспроизводящие установленные единицы физических величин и передающие их соответствующим средствам измерений. Высшим звеном в метрологической цепи передачи размеров единиц являются эталоны.
Эталон единицы - средство измерений (или комплекс средств измерений), предназначенное для воспроизведения и (или) хранения единицы с целью передачи ее размера нижестоящим по поверочной схеме средствам измерений, и утвержденное в качестве эталона в установленном порядке. Классификацию, назначение и общие требования к эталонам устанавливает ГОСТ 8.057-80.
Эталон, обеспечивающий воспроизведение единицы с наивысшей в стране (по сравнению с другими эталонами той же единицы) точностью, называется первичным. Первичные эталоны составляют основу государственной системы обеспечения единства измерений.
Государственный эталон — это первичный эталон, признанный решением уполномоченного на то государственного органа в качестве исходного на территории государства. Государственные эталоны создаются, хранятся и используются центральными метрологическими научными институтами страны. Государственные эталоны подлежат периодическим сличениям с государственными эталонами других стран. Термин "национальный эталон" применяется в случаях проведения сличения эталонов, принадлежащих отдельным государствам или с международным эталоном.
Примером государственного эталона может служить Государственный первичный эталон единицы электродвижущей силы (ГОСТ 8.027—89). Государственные эталоны утверждаются Федеральным агенством по техническому регулированию и метрологии.
Специальный эталон воспроизводит единицу в особых условиях и заменяет при этих условиях первичный эталон. Примером специального эталона является Государственный специальный эталон единицы напряжения переменного тока в диапазоне частот от 100 до 1500 МГц (ГОСТ 8072—73).
Вторичный эталон - эталон, получающий размер единицы непосредственно от первичного эталона данной единицы. Вторичные эталоны являются частью подчиненных средств хранения единиц и передачи их размеров, они создаются в тех случаях, когда это необходимо для организации поверочных работ, а также для
15
обеспечения сохранности и наименьшего износа государственного эталона. Вторичный или рабочий эталон, являющийся исходным для министерства (ведомства), иногда называют ведомственным эталоном.
Эталон сравнения – эталон, применяемый для сличения эталонов, которые по тем или иным причинам не могут быть непосредственно сличены друг с другом. Примером его является так называемый, нормальный элемент, используемый для сличения государственного эталона вольта РФ с эталоном вольта Международного бюро мер и весов.
Рабочий эталон — эталон, предназначенный для передачи размера единицы рабочим средствам измерений. Это самые распространенные эталоны. С целью повышения точности измерений ФВ рабочие эталоны применяются во многих территориальных метрологических органах и лабораториях министерств и ведомств. Рабочие эталоны при необходимости подразделяются на разряды 1-й, 2-й и т.д., определяющие порядок их соподчинения. Для различных видов измерений устанавливается, исходя из требований практики, различное число разрядов рабочих эталонов.
Международный эталон - эталон, принятый по международному соглашению в качестве международной основы для согласования с ним размеров единиц воспроизводимых и хранимых национальными эталонами.
Исходный эталон- эталон, обладающий наивысшими метрологическими свойствами (в данной лаборатории, организации, на предприятии), от которого передают размер единицы подчиненным эталонам и имеющимся средствам измерений. Исходным эталоном в стране служит первичный эталон, исходным для республики, региона, министерства (ведомства) или предприятия может быть вторичный или рабочий эталон.
Рабочее средство измерений – средство измерений, предназначенное для измерений, не связанных с передачей размеров единиц другим средствам измерений.
Поверка средств измерений – установление органом государственной метрологической службы (или другим официально уполномоченным органом, организацией) пригодности средства измерений к применению на основе экспериментально определенных метрологических характеристик и подтверждения их соответствия установлены обязательным требованиям. Основной метрологической характеристикой, определяемой при поверке СИ, является его погрешность. Она находится путем сравнений показаний поверяемого СИ и рабочего эталона.
16
Различают поверку первичную, периодическую, внеочередную, инспекционную, комплексную, поэлементную и выборочную [1]. Основные требования к организации и проведению поверки определены в правилах по метрологии и рекомендациях [2-4]. Поверка выполняется метрологическими службами, которым дано на это право. На средство измерений, признанное годным к применению, выдается свидетельство о поверке и наносится поверительное клеймо.
Градуировка – нанесение отметок на шкалу, соответствующих показаниям рабочего эталона или определения по его показаниям уточненных значений величины, соответствующих нанесенным отметкам на шкале рабочего средства измерений.
Калибровка – совокупность операций, устанавливающих соотношение между значением величины, полученным с помощью данного средства измерений и соответствующего значения величины, определенного с помощью эталона с целью определения действительных метрологических характеристик этого средства измерений. Если средства измерений не подлежат обязательному метрологическому контролю и надзору, то они могут подвергаться калибровке.
По результатам калибровки определяют действительное значение измеряемой величины, показываемое данным средством измерений, или поправки к его показаниям. Калибровка позволяет оценить погрешность средства измерений и ряд других метрологических характеристик.
Метрологическая цепь передачи размеров единиц от первичных эталонов рабочим эталонам, и далее рабочим средствам измерений, показана на рис. 1.1. Передача размеров единиц осуществляется посредством измерений. Утвержденный в установленном порядке документ, определяющий соподчинение средств измерений, участвующих в передаче размера единицы от эталона к рабочим СИ, методы и точность передачи размера единицы от эталона или образцового средства измерений рабочим средствам, называется поверочной схемой и оформляется в виде чертежа и текстовой части. Основные положения о поверочных схемах приведены в ГОСТ 8.061-80 [Л.5].
Поверочные схемы подразделяют на государственные, и локальные. Государственная поверочная схема распространяется на все средства измерений конкретной физической величины, имеющиеся в стране. Государственные поверочные схемы разрабатываются метрологическими институтами, утверждаются в качестве государственных стандартов и состоят из чертежа поверочной схемы и текстовой части, содержащие пояснения к чертежу.
Локальная поверочная схема распространяется на средства измерений данной физической величины, применяемые в данном регионе, отрасли, ведомстве или на
17
отдельном предприятии (организации). Локальные поверочные схемы не должны противоречить государственным поверочным схемам средств измерений одних и тех же физических величин. Локальная поверочная схема может быть разработана и при отсутствии государственной поверочной схемы. На рис. 1.1 представлены различные варианты построения локальных поверочных схем. Обычно в поверочных схемах
даются названия и необходимые сведения о применяемых |
рабочих |
эталонах, |
|
поверяемых СИ и методах передачи размеров физических величин. |
|
|
|
Локальная поверочная схема может быть разработана |
и при |
отсутствии |
|
государственной поверочной |
схемы. На рис. 1.1 представлены |
различные |
|
варианты построения локальных поверочных схем. Обычно в поверочных схемах даются названия и необходимые сведения о применяемых рабочих эталонах, поверяемых СИ и методах передачи размеров физических величин.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рабочий |
|
|
|
|
|
|
Рабочий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рабочий |
|
|
|
||||||||||||||
|
|
|
эталон |
|
|
|
|
|
|
эталон |
|
|
|
|
|
|
эталон |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод |
|
|
|
|
Метод |
||||||||||||
|
|
|
|
|
|
|
Метод |
|
||||||||||||||||||||||||
|
|
|
Метод |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
Передачи |
|
|
|
передачи |
|
|
|
|
передачи |
|
|
|
|
||||||||||||||
|
|
|
передачи |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объект |
|
|
|
|
Объект |
|
||||||
|
|
|
Объект |
|
|
|
|
|
|
|
Объект |
|
|
|
|
поверки 1 |
|
|
|
|
поверки 2 |
|
||||||||||
|
|
|
поверки |
|
|
|
|
|
|
поверки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
а) |
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Рис.1.1
1.6.Метрологическая служба РФ.
Вразвитии отечественной метрологии можно отметить четыре этапа. Первый этап охватывает почти весь XIX век. Этот период характерен активизацией метрологической деятельности и началом широкого участия русских ученых в работе международных метрологических организаций. В 1842 г. на территории Петропавловской крепости в специально построенном помещении было открыто первое централизованное метрологическое и поверочное учреждение России — Депо образцовых мер и весов, в котором хранились эталоны длины и массы (платиновая сажень и платиновый фунт), их копии, а также образцы различных
18
иностранных мер. В Депо изготавливались образцовые меры, проводилась поверка
исличение их с иностранными мерами. Эта деятельность регламентировалась «Положением о мерах и весах» (1842 т.), которое заложило основы государственного подхода к обеспечению единства измерений.
Для русских ученых этого времени характерно глубокое понимание роли места метрологии в науке и жизни. В 1869 г. Петербургская академия наук направила в Парижскую академию наук доклад, в котором предлагалась с целью обеспечения единства измерений в международном масштабе изготовить новые международные прототипы метра и килограмма и распределить их однотипные копии между заинтересованными государствами. Это предложение было принято,
ив результате последующей работы ученых разных стран была подписала 1 марта 1875 г. Метрическая конвенция. Она способствовала унификации мер и расширению метрологической деятельности в национальном и международном масштабе. В соответствии с конвенцией Россия получила платино-иридиевые эталоны единицы массы № 12 и 26 и эталоны единицы длины № 11 и 28.
В1892 г. управляющим Депо был назначен Д. И. Менделеев, который так много сделал для отечественной метрологии, что период с 1892 г. по 1917 г. называют менделеевским этапом развития метрологии. В 1893 г. он преобразует Депо образцовых мер и весов в Главную палату мер и весов - одно из первых в мире научно-исследовательских учреждений метрологического профиля. Лишь через семь лет в Англии было организовано метрологическое отделение Национальной физической лаборатории, а год спустя в США — Национальное бюро эталонов. Под руководством Д. И Менделеева была начата работа по созданию русской системы эталонов и сличению их с английскими и метрическими мерами, а также государственной метрологической службы, реализована широкая программа научных исследований в области метрологии.
Собственные работы Д. И. Менделеева по метрологии не утратили своего значения и в наше время. Ему принадлежит высказывание — «Наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры». Основанные Д.И.Менделеевым научные направления на долгие годы определили пути развития отечественной метрологии, обеспечили ей передовые позиции и высокий авторитет на международной арене. Но даже Д. И. Менделееву не удалось внедрить в России метрическую систему. С 1899 г. она применялась в стране факультативно, наряду со старой русской и британской (дюймовой) системами.
19
Метрическая система была принята декретом «О введении международной метрической системы мер и весов» был принят Советом Народных Комиссаров (СНК) 14 сентября 1918 г. С введением метрической системы начался третий этап в развитии отечественной метрологии, который продолжался до Великой Отечественной войны. Главным его содержанием является переход к государственной метрологической деятельности.
С первых лет Советской власти правительство уделяло большое внимание упорядочению состояния измерений в стране. Ряд постановлений Совета Народных Комиссаров и Совета труда и обороны (СТО) обеспечил систематическое и планомерное развитие научной и организационно-технической деятельности в области метрологии. В 1925 г» СНК СССР принимает постановление «О признании заключенной в Париже 20 мая 1875 г. Международной метрической конвенции для обеспечения международного единства и усовершенствования метрической системы, имеющей силу в СССР». Тем самым возобновлялись международные связи нашей страны в области метрологии. В этом же году создается Комитет по стандартизации при СТО. К 1927 г. завершилась метрическая реформа в СССР.
Четвертый, послевоенный период, характеризуется небывалым размахом всей метрологической деятельности в стране. Отличительной её особенностью является повсеместное внедрение стандартизации как главной организационноправовой формы обеспечения единства измерений. Была разработана и внедрена Государственная система стандартизации (ГСС), Организационные принципы построения и основные задачи метрологической службы страны в рамках ГСС регламентировались Госстандартом. В 1973 г. структура метрологической службы была закреплена основополагающим ГОСТ 1.25—76 «ГСС. Метрологическое обеспечение. Основные положения». В соответствии с этим документом Государственная метрологическая служба состояла из институтов и территориальных органов, возглавляемых Государственным Комитетом по стандартам и республиканскими управлениями.
Главным центром Государственной метрологической службы был назначен Всесоюзный научно-исследовательский институт метрологической службы (ВНИИМС), задачи которого заключались в разработке научно-методических, технико-экономических, организационных и правовых основ метрологического обеспечения и научно-методическое руководство метрологической службой, развитие эталонной базы и образцовых средств измерений, проведение
20
государственных испытаний, стандартизацией в области обеспечения единства измерений, работы по международному сотрудничеству в области метрологии. Главными центрами государственных эталонов были назначены Научнопроизводственное объединение «Всесоюзный научно-исследовательский институт метрологии им. Д. И. Менделеева» (ВНИИМ); Всесоюзный научноисследовательский институт физико-технических и радиотехнических измерений (ВНИИФТРИ), Сибирский государственный научно-исследовательский институт метрологии (СНИИМ) и др.
Внастоящее время единства измерений в РФ основывается на Законе Российской Федерации «Об обеспечении единства измерений», который устанавливает правовые основы обеспечения единства измерений и регулирует отношения государственных органов управления с юридическими и физическими лицами по вопросам производства, эксплуатации и ремонта средств измерений.
Вдекабре 2002 г. Государственной Думой принят Закон Российской Федерации «О техническом регулировании», одобренный Советом Федерации.
Закон направлен на установление правил государственного регулирования требований к продукции, включая товары народного потребления, связанных с нею процессов, а также требований к работам и услугам в интересах потребителей. Закон предусматривает освобождение предпринимателей от мелочной опеки органов исполнительной власти и кардинальное повышение уровня правового регулирования
вважной сфере деятельности. Закон разработан в соответствии с практикой работы в данной области стран с развитой рыночной экономикой, требованиями международных экономических организаций, включая Всемирную торговую организацию. Это обстоятельство является необходимым условием интеграции России
вмировой экономический процесс.
Втерминологическом разделе Закона (статья 2) техническое регулирование определено как - правовое регулирование отношений в области установления, применения и исполнения обязательных требований к продукции, процессам производства, эксплуатации, хранения, перевозки, реализации и утилизации, а также в области установления и применения на добровольной основе требований к продукции, процессам производства, эксплуатации, хранения, перевозки, реализации и утилизации, выполнению работ или оказанию услуг и правовое регулирование отношений в области оценки соответствия.
Всоответствии с Законом РФ «О техническом регулировании» в РФ будут действовать общие и специальные технические регламенты. Технический регламент
21 (статья 2 Закона), это документ, который принят международным договором Российской Федерации, ратифицированным в порядке, установленном законодательством Российской Федерации, или федеральным законом, или указом Президента Российской Федерации, или постановлением Правительства Российской Федерации и устанавливает обязательные для применения и исполнения требования к объектам технического регулирования (продукции, в том числе зданиям, строениям и сооружениям, процессам производства, эксплуатации, хранения, перевозки, реализации и утилизации).
В общих технических регламентах должны содержаться требования, обязательные для применения и соблюдения в отношении любых видов выпускаемой продукции, процессов производства, эксплуатации и утилизации, в частности по вопросам пожарной безопасности, экологической безопасности и другие требования. В специальных технических регламентах будут содержаться требования, учитывающие технические и иные особенности отдельных видов деятельности или продукции.
Закон РФ «О техническом регулировании» изменил некоторые принципы стандартизации, что не может не отразиться на организационных основах метрологического обеспечения в стране. К новым принципам можно отнести то, что стандартизация осуществляется на основе:
-добровольного применения стандартов;
-максимального учета при разработке стандартов законных интересов заинтересованных лиц;
-применения международного стандарта как основы разработки национального стандарта, за исключением случаев, если такое применение признано невозможным вследствие несоответствия требований международных стандартов климатическим и географическим особенностям Российской Федерации, техническим и (или) технологическим особенностям или по иным основаниям;
-недопустимости создания препятствий производству и обращению продукции, выполнению работ и оказанию услуг;
-недопустимости установления таких стандартов, которые противоречат техническим регламентам;
-обеспечения условий для единообразного применения стандартов. Регулирование стандартизации в Законе не означает признание за ней государственного статуса. Однако ряд его положений, однозначно свидетельствуют,
22
что стандартизация является функцией государства, несмотря на добровольность применения стандартов. Придание национальным стандартам статуса необязательных документов не исключает их из круга вопросов, регулируемых государством в лице соответствующих органов РФ. Национальные стандарты, играя роль рекомендаций, являются всё же документами, разработанными по правилам, определённым государством.
Организацию всей работы по стандартизации в РФ согласно Закону осуществляет Национальный орган РФ по стандартизации. Этот орган выполняет ряд функции, главные из которых:
-принятие программы разработки национальных стандартов;
-организация экспертизы проектов национальных стандартов;
-утверждение национальных стандартов;
-создание технических комитетов по стандартизации и координация их деятельности;
- участие в разработке международных стандартов.
-представление РФ в международных организациях, осуществляющих деятельность в области стандартизации.
В Российской Федерации функции национального органа по стандартизации реализует Федеральное агентство по техническому регулированию и метрологии, которое действует на основании Положения о Федеральном агентстве по техническому регулированию и метрологии, утвержденного Постановлением Правительства Российской Федерации от 17 июня
2004 г. №294.
К основным задачам федерального агентства по техническому регулированию и метрологии относятся:
-реализация функций национального органа по стандартизации;
-обеспечение единства измерений;
-осуществление работ по аккредитации органов по сертификации и испытательных лабораторий (центров);
-осуществление государственного контроля (надзора) за соблюдением требований технических регламентов и обязательных требований стандартов;
-создание и ведение федерального информационного фонда технических регламентов и стандартов и единой информационной системы по техническому регулированию;
-оказание государственных услуг в сфере, стандартизации, технического
23
регулирования и метрологии.
Федеральное агентство осуществляет свою деятельность непосредственно и через подведомственные ему организации, которые составляют единую систему, в которую входят:
- Центральный аппарат; -Федеральные государственные учреждения - центры стандартизации,
метрологии и сертификации;
-Научно-исследовательские институты;
-Опытные заводы;
-Территориальные органы;
-Учебные заведения и другие организации.
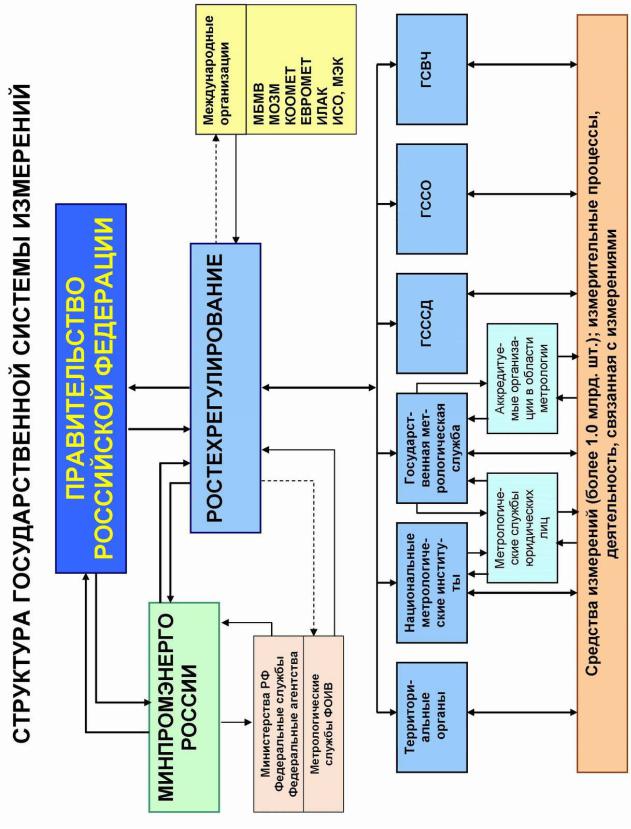
Структура Государственной системы измерений поясняющая взаимодействие в этом вопросе правительства РФ, Министерств РФ, Федеральных служб, и Федеральных агенств, представлена на рис. 1.2.
Основная функция Правительства Российской Федерации в области метрологии заключается в формировании в стране такого положения, при котором обеспечивается доверие к результатам измерений и эффективная защита от недостоверных измерений, а также – непрерывное развитие метрологии, достаточное для решения приоритетных, перспективных задач в жизненно важных сферах Российской Федерации.
На Минпромэнерго России возложена обязанность по выработке государственной политики и нормативно – правовому регулированию в области обеспечения единства измерений.
Ростехрегулирование выполняет функции по оказанию государственных услуг и управлению государственным имуществом в сфере метрологии, осуществлению государственного метрологического надзора, а также по межотраслевой и межведомственной координации в области обеспечения единства измерений и взаимодействию в установленном порядке с международными организациями в сфере метрологии. При этом Ростехрегулирование определен подведомственным Минпромэнерго России.
24
Рис 1.2.
25
Выполнение своих функций Ростехрегулирование осуществляет с помощью организационной структуры изображенной на рис. 1.2. и включающей:
национальные метрологические институты (всего 7); государственные службы по обеспечению единства измерений в Российской
Федерации (всего 4); центры стандартизации и метрологии в субъектах Федерации (всего 86),
выполняющие функции территориальных органов государственной метрологической службы;
территориальные органы Ростехрегулирования (всего 7); аккредитованные организации на компетентность в области метрологии (более
6500);
метрологические службы (МС) федеральных органов исполнительной власти (ФОИВ);
метрологические службы юридических лиц; государственная служба стандартных справочных данных (ГСССД); государственная служба стандартных образцов (ГССО); государственная служба времени и частоты (ГСВЧ).
Структура ГСИ в части, которая управляется Ростехрегулированием, складывалась в течение последних 10 лет и практически не претерпела изменений при административной реформе.
Отрасль «Связь» по использованию средств измерений занимает одно из ведущих мест среди других отраслей. Это объясняется целым рядом факторов, главные из которых заключаются в следующем:
широкий диапазон частот измеряемых колебаний, который простирается от нулевых частот (измерение постоянного тока и напряжения) до частот лазерного излучения;
широкий диапазон измеряемых физических величин (напряжения, тока, мощности), который начинается с долей микровольт, микроампер и микроватт и простирается до сотен киловольт, ампер и киловатт;
наличие большого количества узкопрофильных средств измерений, таких как приборы для оценки правильности функционирования цифровых сетей связи, приборы для измерений в области телевидения (включая световые измерения), звукового вещания (включая акустические измерения) и т.п.;
средства связи в нашей стране распространены на громадной территории, выполняя не только задачи обслуживания населения, но и задачи обеспечения
26
эффективного функционирования других отраслей – железнодорожного и авиационного транспорта, нефтяной и газовой промышленности, электроэнергетики и др.;
широкий диапазон климатических условий функционирования средств связи, а следовательно и средств измерений, используемых как при строительстве объектов связи, так и при их эксплуатации.
Ведомственная метрологическая служба Министерства связи и информатизации в своей деятельности взаимодействует с Федеральным агенством по техническому регулированию и метрологии и его службами, а так же с национальными метрологическими институтами. В их числе ФГУП Всероссийский научно - исследовательский институт метрологической службы (ВНИИМС), ФГУП Всероссийский научно – исследовательский институт метрологии им. Д. И. Менделеева (ВНИИМ), ФГУП Всероссийский научно - исследовательский институт физико-технических и радиотехнических измерений (ВНИИФТРИ), ФГУП Всероссийский научно - исследовательский институт оптико-физических измерений (ВНИИОФИ).
Научные и практические вопросы метрологии в отрасли связь разрабатывают в научно-исследовательских институтах отрасли: ФГУП Центральный научноисследовательский институт связи (ЦНИИС), ФГУП Научно-исследовательский институт радио (НИИР). ЦНИИС является головной научно-исследовательской организацией и одновременно базовой организацией по вопросам измерений в проводной связи, НИИР – базовой организацией по измерениям в радиосвязи.
1.7.Планирование измерительного эксперимента. Модели объекта и измерительных сигналов.
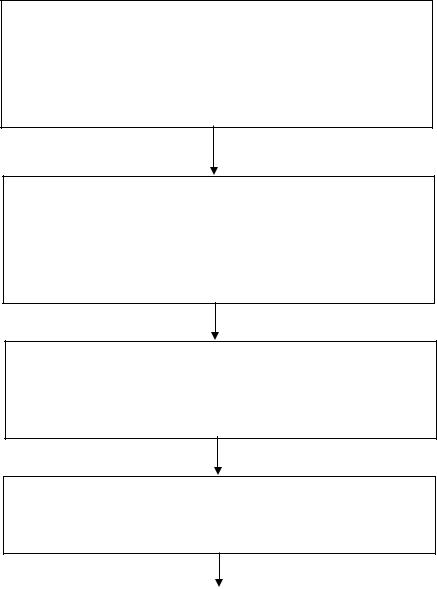
Всякая измерительная процедура выполняется с целью экспериментального исследования свойств изучаемого объекта. При правильной постановке эксперимента, он, прежде всего, должен быть спланирован. Последовательные этапы планирования и проведения эксперимента представлены на рис.1.3
27
1
Изучение объекта измерений и его свойств. Определение порядка измеряемых величин. Обоснование необходимой точности (или допустимой погрешности) измерений. Подбор модели измеряемого объекта.
2
Выбор моделей измерительных сигналов, необходимых для проведения измерений с требуемой точностью
3
Разработка программы измерений. Выбор средств измерений.
4
Проведение измерений, составление протокола.
Рис.1.3
5 |
Рис.1.3. |
Анализ результатов измерений оценка погрешностей. |
|
|
|
Изучение объекта измерений до их проведения является совершенно необходимым. Конечно, речь идет о достаточно сложных объектах. Но даже простые измерительные задачи иногда не имеют решения. Например, может так случиться, что невозможно взвесить ровно 1 кг болтов при их покупке, если конечно, речь идет о их целом числе. Чем больше масса отдельного изделия, тем больше может быть отклонение от необходимой величины массы. В данном случае измеряемый объект имеет дискретную структуру и погрешность, с которой может быть решена задача, приближается к величине ±m - массе отдельного изделия. Если допустить такую погрешность, то, очевидно, нет смысла использовать высокоточные весы. Может быть и другое решение: следует отказаться от задачи взвешивания массы ровно в 1 кг,
28
взвесить несколько больше или меньше и учесть эту разницу при определении стоимости товара. Здесь то же может не быть абсолютно точного решения, поскольку имеется дискретность денежной единицы в 1 копейку. Безусловно, второе решение рациональнее и на практике так и поступают.
В случае сложных объектов, с которыми приходится иметь дело в технике связи, выбор оптимального решения не так очевиден, и реальный объект обычно заменяется его моделью. К сожалению, большинство инженеров, имеющие дело с измерениями, забывают, что, разрабатывая методику измерений, они фактически имеют дело с моделью объекта, которая не является абсолютно точной и не отражает всех его свойств.
При моделировании используются процедуры абстрагирования и идеализации. Эта особенность моделирования особенно существенна, когда речь идет о сложных системах, поведение которых зависит от большого числа взаимосвязанных факторов различной природы. К таким системам, безусловно, относятся системы телекоммуникаций. Используя при разработке таких систем уравнения Максвелла и определенные граничные условия, детерминированные функции непрерывного времени и преобразования Фурье, Лапласа, Котельникова, мы имеем дело с моделями реальных процессов.
От правильного выбора модели, являющейся основой гипотезы о свойствах реального объекта, степени её адекватности объекту зависит обоснованность выводов, объективность оценки состояния объекта исследования и достоверность прогнозирования.
Значение применяемой при измерениях модели, даже на начальной стадии изучения метрологии, можно оценить на простом примере. Представим себе, что на токарном станке изготовлена некоторая деталь, размеры которой подлежат измерению. В первом представлении моделью детали может служить прямой круговой цилиндр. Требуется измерить диаметр (порядка 10 мм) с требуемой в документации точностью.
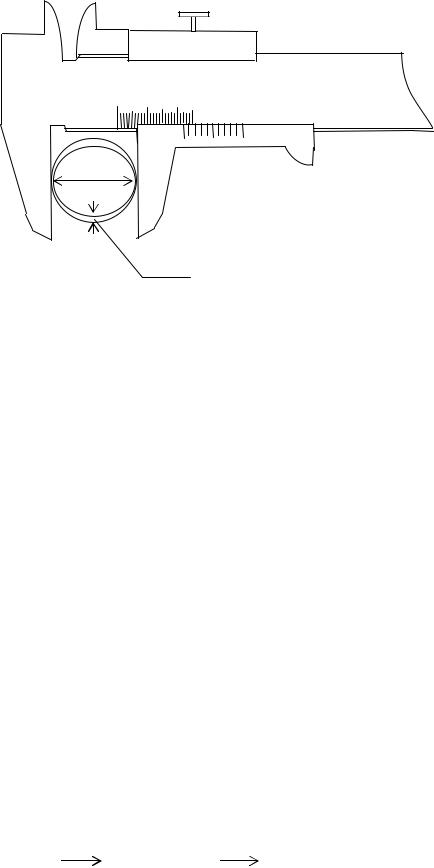
29
0,1 мм
0 1 2
d
Рис. 1.4.
Если задано требование найти диаметр с погрешностью ± 1 мм, то модель «круг», несомненно, адекватна объекту, имеет физический смысл и результат может быть получен одним измерением с помощью простого штангенциркуля, как показано на рис. 1.4. При таком допуске результаты измерений, проведенные по различным направлениям, вероятнее всего совпадут. Иначе обстоит дело, в случае если допустимое отклонение не должно превышать ± 1 мкм. Как видно из рис.1.4., действительная форма объекта, отображенная пунктирной линией, имеет эллиптичность и если отклонение от диаметра модели –d, обозначенное , существенно превышает 1 мкм, поставленная задача не имеет решения, так как при повороте детали будет получатся каждый раз новый результат. Неравенство результатов измерений выявит неадекватность модели (круга) объекту и как следствие, отсутствие физического диаметра, так как диаметр присущ только кругу и может иметь только одну величину. Никаким совершенствованием метода измерений нельзя найти диаметр, так как его физически нет.
При проведении измерений в технике связи широко используются измерительные сигналы. Основная идея применения измерительных сигналов иллюстрируется рис. 1.5.
Источник |
|
Исследуемый |
|
Измерительный |
измерительного |
|
объект |
|
прибор |
сигнала |
|
|
|
|
(генератор) |
|
|
|
|
|
|
Рис. 1.5 |
|
|
30
Как видно из рис.1.5., на исследуемый объект воздействует измерительный сигнал, поступающий от генератора. Выбор типа генератора, и соответственно, измерительного сигнала, определяется теми свойствами объекта, которые необходимо изучить. Например, если объектом является усилитель аналоговых сигналов, то вероятнее всего в качестве генератора следует применить генератор гармонического сигнала с соответствующим диапазоном частот и с требуемой амплитудой сигнала. Выбирая сигнал, мы выбираем фактически его модель, так как невозможно создать генератор, вырабатывающий абсолютно точно гармонический сигнал. Допустимые отклонения формы реального сигнала определяются поставленной измерительной задачей. Последним звеном является измерительный прибор – анализатор отклика исследуемого объекта на измерительный сигнал. Его выбор определяется тем параметром выходного сигнала, который несет в себе искомую информацию об исследуемом объекте. Возможно, что в ходе эксперимента измерительные приборы будут меняться, или к выходу исследуемого объекта будет подключено сразу несколько приборов (например, вольтметр, измеритель нелинейных искажений, осциллограф и др.)
Результатом проведенной работы будут данные о свойствах исследуемого объекта, точность и достоверность которых в значительной степени будут зависеть от того, насколько измерительный сигнал соответствует принятой модели. Каким образом даже небольшие отклонения реального сигнала от принятой модели влияют на результат измерения можно видеть из следующего простого примера, смысл которого ясен даже для читателя неискушенного в тонкостях метрологии.
Предположим, что согласно схеме рис.1.5., проводится измерение частотной характеристики фильтра, т.е. зависимости затухания фильтра от частоты. Таким образом, фильтр является объектом исследования. В этом случае в качестве источника сигнала используется перестраиваемый по частоте генератор гармонического сигнала, а качестве измерительного прибора обычный вольтметр. Предположим, что расчетная характеристика затухания фильтра имеет вид, представленный на рис. 1.6.
αдБ
60 дБ
1 дБ
ω1 |
2ω1 |
ω |
Рис.1.6.
31
Для измерения затухания на частоте ω1 необходимо установить сигнал на входе исследуемого объекта- Uвх и измерить сигнал на выходе - Uвых . Затухание, вносимое фильтром, определится из соотношения:
α = 20 lg Uвх/ Uвых
Предположим, что входной сигнал определяется выражением Uвх= 100 sin ω1 t.
Будем считать, что амплитуда сигнала составляет 100 мВ. Поскольку на частоте ω1
затухание составляет 60 дБ (т.е. сигнал ослабляется в 1000 раз), измерительный прибор должен показать напряжение 0,1 мВ.
Положим, что измерительный сигнал, вырабатываемый генератором в действительности не является чисто гармоническим и содержит вторую гармонику, т.е.
Uвх= Uвх1+ Uвх2= 100 sin ω1 t +2 sin 2ω1 t.
Как видно из последнего выражения амплитуда второй гармоники составляет всего 2 мВ и, следовательно, на первый взгляд не сможет повлиять на результат измерения, т.к. составляет всего 2% от величины основного сигнала. Проверим, что же будет в действительности. Величина первой гармоники как в первом случае уменьшится в 1000 раз и составит 0,1 мВ. Амплитуда второй гармоники изменится значительно меньше.
Как видно из рис.1.6 частоте 2ω1 соответствует минимум кривой затухания. Затухание для неё всего 1 дБ (т.е. она ослабляется всего в 1,12 раза) и амплитуда составит 2/1,12=1,78 мВ. Таким образом, вторая гармоника на выходе устройства оказалась в 1,78/0,1=17,8 раза больше основной. Если пренебречь основной гармоникой, то можно считать, что прибор покажет напряжение 1,78 мВ., следовательно, затухание окажется равным
α= 20 lg 100/ 1,78 = 35 дБ.
Совершенно очевидно, что проведенный эксперимент нельзя считать удовлетворительным. Слишком далек полученный результат от правильного значения, которое составляет 60 дБ. Следует обратить внимание, что отличие реального сигнала, от его модели весьма незначительное. Вторая гармоника имеет амплитуду, которая, составляет всего 2% от основной гармоники! Большая погрешность измерения

32
безусловно связана с особенностями исследуемого объекта. Так случилось, что минимум кривой затухания пришелся точно на частоту второй гармоники.
При исследовании других объектов такой погрешности может и не быть. Однако приведенный пример показывает, на сколько тщательно необходимо изучать особенности исследуемого объекта и правильно подбирать измерительную аппаратуру. Это касается не только генератора, но и вольтметра. Погрешность измерения можно существенно уменьшить, если, не меняя генератора, выбрать в качестве прибора, измеряющего напряжение на выходе исследуемого, объекта избирательный (селективный) вольтметр и при проведении измерений настроить его на частоту первой гармоники.
Модели измерительных сигналов
1.Прямоугольный импульс
Графическое определение |
|
Аналитическое определение |
|
|||||||||||
х |
|
|
|
|
|
|
|
|
0; |
t |
<0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
b |
|
|
с |
|
|
||||||
Ап |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
А ; 0≤t≤τ |
П |
|||
|
|
|
|
|
|
|
|
|
|
x(t) = |
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
0; t > |
τ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
а |
|
τп |
|
|
|
|
П |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
τп-длительность прямоугольного импульса ( ПИ) Ап- пиковое значение прямоугольного импульса.
Отрезок аb называют фронтом ПИ, bc- вершиной ПИ, cd- срезом ПИ.
2. Трапецеидальный импульс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Графическое определение |
|
|
|
|
|
|
|
|
|
Аналитическое определение |
|
|||||||||||
|
|
|
|
АТ-пиковое значение трапецеидального импульса (ТИ), τТ –длительность ТИ, |
||||||||||||||||||
|
|
|
|
τф –длительность фронта ТИ, τс- длительность среза ТИ. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
х |
|
|
|
|
|
|
|
|
|
0; t < 0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
; 0 ≤ t ≤τ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
τс |
|
|
ф |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
АТ |
|
b |
c |
|
|
|
|
|
|
|
Т |
τф |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
АТ |
; τф ≤ t ≤τ −τc ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) = |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
d |
t |
|
|
|
|
t −τТ +τ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
τ-τС |
τ |
Т |
|
|
|
− |
с |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
τф |
|
|
|
|
|
АТ |
1 |
τс |
|
|
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−τс ≤ t ≤τТ ; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τТ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ; t ≥τТ |
|
|
|
||||

33
3.Пилообразный импульс
Графическое определение
|
|
|
х |
|
Апл |
b |
|
|
|
|
|
|
|
|
c t |
|
|
|
|
|
a |
||
|
|
|
τпл |
|
|
|
|
Апл- пиковое значение пилообразного импульса (ПЛИ),
τпл-длительность пилообразного импульса. Отрезок ab-называется прямым ходом ПЛИ, bc –обратным ходом ПЛИ.
Аналитическое определение
|
|
|
|
|
0; t <0 |
||||
|
АПЛ |
t |
|
|
x(t) = |
;0 ≤t ≤τПЛ ; |
|||
|
|
|||
τПЛ |
|
|
||
|
|
≥τПЛ |
||
0;t |
||||
4. Треугольный импульс |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Графическое определение |
Аналитическое определение |
|||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0;t <0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
b |
АТГt |
|
|
|
|
|
|
||||||||
|
Атг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
;0 |
≤t ≤τФТ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t −τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФТ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
x(t) = |
|
|
|
|
;; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
АТГ 1 − |
τСТ |
|
||||||||
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τфт |
|
|
|
τст |
|
|
|
τФТ ≤ t ≤τТГ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0;t >τТГ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
τтг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отрезок аb-называется фронтом треугольно импульса (ТИ), отрезок bcсрезом ТИ
34
5. Колоколообразный импульс |
|
|
|
|
|
|
||||
Графическое определение |
Аналитическое определение |
|||||||||
|
Ак |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
t |
2 |
||
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
x(t) = А е |
|
|
|
к |
|
|
|
|
0 |
t |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2τк |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Ак −пиковое значение колоколообразного импульса 2τк −интервал времени между точками перегиба колоколообразного
импульса (определяются также по уровню 0,606 |
Ак |
|
|
|
|
|
|
|
|
||||||||||
6.Косинусквадратный импульс |
|
|
|
|
|
|
|
|
|
||||||||||
Графическое определение |
Аналитическое определение |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Ас |
|
|
|
|
|
|
|
x(t) = A |
cos2 |
π |
t ; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
τc |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
−τс ≤t ≤τc ; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τc |
|
|
|
|
|
|
|
0 |
|
|
|
t |
0 ; |
|
t |
|
> |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
τc/2 |
|
|
|
τc/2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ас -пиковое значение косинусквадратного импульса; τс - длительность косинусквадратного импульса. (Значение параметраτс определяется также по уровню Ас )
35
7. Гармонический сигнал
Графическое определение |
Аналитическое определение |
x
x(t) = A sin(ωt +ϕ);
−∞<t <∞
A
0
 t
t
φ/ω |
|
Т = |
2π |
|
ω |
||
|
|
|
А – амплитуда гармонического сигнала; ω- круговая частота; φ- начальная фаза
8. Периодическая последовательность прямоугольных импульсов
Графическое определение |
|
Аналитическое определение |
|
||||||||||||||
x |
|
|
|
|
|
|
|
|
A |
,kT ≤ t ≤kT +τ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) = П |
|
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
АП |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0, kT +τП <t <kT =T |
|||||
τП |
|
|
|
|
|
|
|
|
|
|
t |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|||
Отношение |
Т |
−называется скважностью, а обратная величина – |
|
||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
τП |
Т |
|
|
|
|||||||
коэффициентом заполнения. При |
= 2 периодическая последовательность |
||||||||||||||||
τП |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
импульсов называется меандром.
9.Реальные измерительные сигналы и их отличие от моделей.
При планировании и проведении измерений приходится учитывать отличие реальных сигналов, от сигналов рассмотренных ранее. В процессе формирования и при различных преобразованиях сигналов происходит искажение их формы. Как правило, не всегда принципиально возможно формирование идеальных сигналов в соответствии с
36
принятыми моделями. Так, например, невозможно формирование фронта импульса с длительностью равной нулю. В реальной аппаратуре имеются паразитные емкости, из-за которых мгновенный скачок напряжения невозможен. Принципиально невозможно сформировать идеально линейную зависимость напряжения от времени. Обычно такое напряжение формируется с помощью заряда или разряда конденсатора, однако реальные цепи имеют сопротивление, поэтому заряд и разряд конденсатора осуществляется не по линейному, а по экспоненциальному закону. Возможна коррекция нелинейности, однако остаточная нелинейность всегда имеет место.
При усилении сигналов возникают линейные, фазовые и нелинейные искажения.. Сигналы по разному реагируют на эти искажения. Так, например, частотные искажения (спад или подъем частотной характеристики в области нижних и верхних частот) могут существенно изменить форму импульсов, однако при этом совершенно неизменной будет форма гармонического сигнала. В то же время нелинейные искажения (например, ограничение сигнала) не повлияют на форму прямоугольного импульса, однако сразу проявятся на гармоническом сигнале.
Подверженность измерительных сигналов искажениям вовсе не является их недостатком. Наоборот, при проведении измерений именно по изменениям формы измерительных сигналов судят о характеристиках исследуемых объектов, однако до входа измерительного объекта сигнал по возможности должен приближаться к идеальному сигналу, т.е. соответствовать модели. Что происходит при искажении измерительного сигнала до его попадания на исследуемый объект, было уже рассмотрено на рис. 1.6. В связи с тем, что существует устоявшаяся терминология не только применительно к измерительным сигналам, но и их искажениям, рассмотрим форму прямоугольного импульса, в том виде в котором она обычно воспроизводится на экране осциллографа.
u

 δП
δП
АП |
0,9АП |
|
|
|
0,1АП |
 t
t
τФ τс
Рис. 1.13
37
На рис. 1.13 –τф- длительность фронта импульса, которая оценивается как время нарастания сигнала от уровня 0,1 АП до 0,9 АП, δП -неравномерность вершины прямоугольного импульса. Как видно из рис. 1.13., осциллограмма импульса имеет выброс как после фронта импульса, так и после его спада. Так как перечисленные искажения формы импульса вызываются разными причинами, целесообразно рассматривать их отдельно, связав с конкретными явлениями, происходящими в электрических цепях.

38
Глава 2. Погрешности измерений
Основные понятия.
При любом измерении неизбежны, обусловленные различными причинами, отклонения результатов измерений от истинного значения измеряемой величины. Истинное значение является объективной оценкой объекта. Результаты измерения представляют собой приближённые оценки значений величин, найденные путём измерения. Они зависят от метода измерения, от средств измерений, от оператора.
Погрешность измерения – отклонение результата измерения от истинного значения измеряемой величины. Различают абсолютную и относительную погрешность измерения. Абсолютная погрешность измерения равна разности между результатом измерения А и истинным значением измеряемой величины Х:
= A− X (2.1)
Относительная погрешность измерения представляет собой отношение (в
процентах) абсолютной погрешности измерения к истинному значению измеряемой
величины: |
|
δ = X |
(2.2) |
Для определения погрешностей по формулам необходимо знать истинное значение измеряемой величины Х. Поскольку истинное значение измеряемой величины неизвестно, для получения приближённых сведений о погрешностях приходится в приведенные выше формулы подставлять так называемые действительные значение. Под действительным значением измеряемой величины понимаёт её значение, найденное опытным путём и настолько приближающиеся к истинному, что для данной цели оно может быть использовано вместо него.
Абсолютная погрешность измерения выражается в тех же единицах, что и измеряемая величина, относительная погрешность безразмерна. К причинам возникновения погрешностей относят несовершенство метода измерений, технических средств, применяемых при измерениях, и органов чувств человека-оператора. В отдельную группу объединяются погрешности, связанные с внешними условиями проведения измерений. Температура окружающей среды, влажность и другие внешние факторы влияют на измеряемые величины и на работу измерительных приборов.
Погрешности измерений имеют случайную и систематическую составляющие. Составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины, называется случайной погрешностью измерения. Случайная погрешность определяется факторами, проявляющимися нерегулярно с
39
изменяющейся интенсивностью. Значение случайной составляющей невозможно предвидеть и, следовательно, невозможно исключить. Влияние случайной погрешности уменьшают применением многократных измерений. Отдельные результаты измерений могут иногда сильно отличаться от ожидаемых, что вызывается кратковременным и сильным воздействием какого-либо фактора (например, броском напряжения питания сети). Возникающая при этом погрешность, существенно превышающая ожидаемую, называется грубой погрешностью измерения.
Кроме случайных имеются погрешности, которые при повторных измерениях остаются неизменными или закономерно изменяются. Такие погрешности называются систематическими. В качестве примера можно привести погрешность, связанную с несоответствием действительного значения меры, с помощью которой осуществляются измерения, её номинальному значению. Систематические погрешности в ряде случаев можно вычислить и исключить из результата измерения. Систематические погрешности классифицируют в зависимости от причин возникновения и по характеру проявления в процессе измерений.
Методическая погрешность – составляющая погрешности измерения, происходящая от несовершенства метода измерений.
Инструментальная (аппаратурная) погрешность измерения – составляющая погрешности измерения, зависящая от погрешностей применяемых средств измерений.
Внешние погрешности, обусловлены внешними по отношению к прибору влияниями, т.е. условиями, при которых происходят измерения.
Субъективные погрешности – составляющие погрешности измерения, обусловленными индивидуальными особенностями оператора. Например, погрешность интерполяции при отсчёте показания.
Помимо понятия погрешности измерения, широко используются понятие точности измерения, являющееся характеристикой качества измерения и отражающего близость его результата к истинному значению измеряемой величины. Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Например, если погрешность измерения равна 10-2 %=10-4 , то точность равна 104.
2.1.Систематические погрешности.
Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематические погрешности вызываются неслучайными факторами, состав которых зависит от конструктивных особенностей средств измерений, условий их
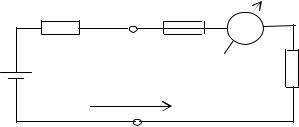
40
применения, а также индивидуальных качеств наблюдателя. Иногда систематические погрешности подчиняются сложным детерминированным закономерностям, которые определяются либо в процессе разработки средств измерений и комплектации измерительной аппаратуры, либо в процессе подготовки и проведения измерительного эксперимента. Совершенствование СИ, методов измерений, применение совершенных материалов позволяют существенно уменьшить влияние систематических погрешностей и в ряде случаев свести к минимуму, настолько, что при обработке результатов измерений с ними можно не считаться.
Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру проявления при измерениях.
2.1.1. Методические погрешности.
Методические погрешности (иногда их называют теоретическими погрешностями), проистекают из-за ошибочности или недостаточной разработки принятого метода измерения. Теоретическое обоснование принятого метода измерения всегда опирается на определенные допущения и упрощения. Так, например, часто прибегают к экстраполяции свойств измеренных на ограниченной части объекта, ко всему объекту. Если эти свойства неоднородны, то возникает методическая погрешность. В технике связи такие проблемы могут возникнуть при измерении параметров протяженных объектов, например кабелей.
К методическим погрешностям следует отнести те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Получаемые при этом результаты становятся настолько приближенными или даже недействительными, как только СИ отключаются от измеряемого объекта. Возникновение методической погрешности из-за взаимодействия СИ с объектом можно проследить на следующем простом примере.
Предположим, что измеряется сила тока, протекающего по последовательной цепи, показанной на рисунке 2.1.1.
Ri |
|
А |
RA |
Rн |
|
E |
|
i
Рис.2.1.1
41
На этом рисунке. пунктиром показан резистор RА, представляющий на схеме эквивалентное сопротивление амперметра. Если пренебречь этим сопротивлением, то ток, протекающий в последовательной цепи, может быть рассчитан с помощью выражения:
i = |
E |
|
|
. |
|
Ri + RН |
||
Это формула определяет значение тока до включения амперметра в состав цепи. При включении амперметра необходимо учесть его внутреннее сопротивление RА и формула принимает следующий вид:
i1 = |
E |
. |
|
Ri + RН + RA |
|||
|
|
Ясно, что ток i1 < i , однако величина неравенства зависит от соотношений между RА и
суммой Ri + RН .
Определим относительную погрешность измерения тока в цепи:
δ = |
i − i1 |
100 = ( 1 − |
|
Ri + RН |
|
)100. |
||
i |
R |
|
|
|||||
|
|
+ R |
Н |
+ R |
A |
|||
|
|
|
i |
|
|
|||
Из выведенной формулы ясно, что если RА составляет малую часть от суммарного сопротивления последовательной цепи, включая сопротивление источника напряжения и нагрузки, то им можно пренебречь и исключить из знаменателя. При этом относительная погрешность будет равна нулю. Иначе обстоит дело если сопротивление амперметра соизмеримо с сопротивлением цепи. Например, если положить общее сопротивление цепи включая сопротивление источника и нагрузки равным 1 Ом, а сопротивление амперметра 0,1 Ом, то погрешность составит 9,1%, т.е. является существенной.
Из данного примера следует, что при определенных сочетаниях параметров измеряемого объекта и средств измерений возникает достаточно большая систематическая погрешность. Следует подчеркнуть, что в примере использована типовая схема измерения тока с помощью амперметра. Из данного примера следует, что даже, применяя измерительные приборы по их прямому назначению и используя типовые схемы, следует внимательно оценивать возможные методические погрешности.
Следует отметить, однако, что данную погрешность можно устранить из результата измерений, если воспользоваться законом Ома и увеличить результат, считанный со шкалы
42
амперметра на некоторую величину. В метрологии этот процесс называется введением поправки. Сложение или вычитание поправки и результата измерений, а так же умножение результата измерений на поправочный множитель позволяет «исправить» результат измерений. Однако не всегда это сделать достаточно просто. Даже в рассмотренном нами случае, хотя поправка рассчитается на основе элементарной формулы, получение её может оказаться проблематичным, поскольку необходимо знание точных значений всех входящих в ее состав сопротивлений. Конечно, сопротивления можно измерить, но тоже с погрешностями. Иными словами решаемая задача заменяется другой измерительной задачей, решение которой может оказаться не менее сложным.
2.1.2. Инструментальные погрешности.
Этот тип погрешностей определяются свойствами применяемых СИ. При разработке СИ преобразования информационного измерительного сигнала осуществляется по определенному алгоритму. Не всегда, из-за трудностей реализации, используется точный алгоритм преобразований. Например, при косвенных методах измерений точная функция преобразования не всегда может быть реализована в приборе из-за технических трудностей и используется метод аппроксимации, что и приводит к погрешности. Кроме того, сама аппроксимирующая функция не может быть точно реализована из-за технологических погрешностей в процессе производства прибора, из-за разброса параметров комплектующих изделий и т.п.
Всем СИ, имеющим шкалу, в большей или меньшей степени присущи погрешности, возникающие в результате неточности нанесения отметок шкалы, так называемые погрешности градуировки. В тех случаях, когда деления шкалы строго равномерны, отметки на шкалы наносятся механически с помощью соответствующих приспособлений. Несовершенство конструкции, износ или неисправности этих приспособлений могут привести к тому, что некоторые отметки окажутся смещенными в ту или иную сторону. При этом в процессе измерений результаты всегда будут содержать ту или иную погрешность.
Более или менее точные измерительные приборы, шкалы которых неравномерны, градуируются на первых этапах часто вручную. Процесс градуировки осуществляется следующим образом. Градуируемый измерительный прибор с основанием, подготовленным для нанесения шкалы, и образцовый измерительный прибор, погрешности которого значительно меньше погрешностей предельно допускаемых для градуируемого прибора, подключают к регулируемому источнику измеряемой величины. Устанавливая различные значения измеряемой величины по показаниям образцового измерительного прибора,
43
одновременно наносят отметки на шкалу градуируемого измерительного прибора. Уже на данном этапе возможно появление погрешностей, например вследствие того, что исполнитель при нанесении отметки будет смотреть не строго перпендикулярно к плоскости шкалы. В результате отметка окажется смещенной либо влево, либо вправо от правильного положения (погрешность из-за параллакса). При градуировке на шкалу наносят только основные или числовые отметки, т.е. отметки, против которых ставят числовые обозначения.
Промежуточные отметки в соответствии с характером шкалы наносят на глаз или с помощью приспособлений различной степени сложности. На этом этапе возможно появление погрешностей градуировки вследствие глазомерных ошибок или несовершенство приспособления, недостаточно точно воспроизводящего в малых делениях характер неравномерности шкалы. Эти погрешности опасны тем, что при поверке прибора, как правило, ограничиваются сличением их показаний с показаниями образцовых СИ также только на числовых отметках. Таким образом, систематические погрешности на промежуточных отметках могут остаться незамеченными.
Большинство современных стрелочных приборов изготовляются с применением печатных шкал (типографским, фотоспособом), однако и в этом случае погрешность градуировки остается. В процессе эксплуатации приборов вследствие износа деталей, старения материала, нарушения регулировки суммарная погрешность может выйти за установленные пределы.
2.1.3. Инструментальные погрешности, являющиеся следствием износа, старения или неисправности СИ.
Износ и старение материалов могут быть причиной появления систематических погрешностей. СИ изнашиваются непрерывно и постепенно со скоростью, зависящей от интенсивности эксплуатации. Следовательно, и погрешности, как правило, возрастают постепенно. Однако этот рост происходит настолько медленно, что в определенный отрезок времени мы можем принимать погрешности, явившиеся следствием износа, постоянными и даже пользоваться соответствующими поправками. Только тогда, когда эти погрешности достигнут определенного порога, дальнейшее применение данного СИ считается недопустимым.
Несколько иначе обстоит дело со старением. Под старением, понимается изменение каких либо свойств материалов с течением времени, а иногда и в зависимости от условий применения или хранения. Процесс старения может протекать различно. Старение может привести к потере каких-либо свойств или к их стабилизации. Одним из характерных
44
примеров старения второго вида является старение манганина. Манганинэто сплав меди, марганца, никеля и некоторых других компонентов. Обладая сравнительно большим удельным электрическим сопротивлением, манганин в то же время имеет малый температурный коэффициент сопротивления. Однако манганин имеет одно отрицательное свойство- с течением времени его сопротивление хотя и медленно, но изменяется. По истечении времени (двух-трех лет) процесс практически прекращается и сопротивление изделия из манганина стабилизируется. Были разработаны приемы искусственного ускорения процесса старения манганина, стабилизации его свойств. Так как полной стабилизации добиться не удается, то для более точных приборов первые годы эксплуатации проводят более частые поверки. В особо ответственных случаях готовое изделие выдерживают годами без применениядо полной стабилизации его свойств, например катушки сопротивления высшей точности. К причинам появления систематических погрешностей можно также отнести перегрузки - механические, электрические, тепловые, вызывающие остаточные изменения в материале или в механизме СИ.
Неисправности, ведущие к появлению небольших систематических погрешностей, гораздо опаснее тех, которые вызывают большие погрешности, которые быстро обнаруживаются «на глаз», по значительному несоответствию результатов измерений ожидаемым. Небольшие систематические погрешности, которые, однако, в два-четыре раза могут превышать допустимые, могут в течение длительного времени оставаться незамеченными.
Особую опасность появление или изменение систематических погрешностей в образцовых средствах измерений, применяемых для поверки других средств измерений. Мало того, что каждое СИ, поверенное или отградуированное с помощью такого образцового СИ, с самого начала будет нести в себе скрытую погрешность, оно будет передавать эту погрешность всем объектам, которые по этому прибору будут измеряться или поверяться. Если вред, приносимый скрытой систематической погрешностью рабочего СИ, можно было бы выразить математически, то для выражения вреда, приносимого систематической погрешностью образцового СИ, это выражение следовало бы возвести в квадрат или даже в четвертую степень для случая поверки образцового СИ следующего, более низкого разряда.
2.1.4. Погрешности, возникающие вследствие неправильной установки СИ, их неправильным взаимным расположением, влиянием внешних воздействий.
Правильность показаний ряда СИ зависит от их положения в пространстве. К ним относятся все СИ, принцип действия которых связан с механическим равновесием.
45
Отклонение такого СИ от правильного положения, которое указывается в технической документации, может привести к прямому или косвенному искажению его показаний. Неудачная взаимная установка СИ может привести к их влиянию друг на друга через магнитные и электрические поля, тепловые воздушные потоки, вибрации, ионизирующие излучения и т.п. Наибольшую опасность представляют величины, действующие непрерывно в течение процесса измерения. Они вносят систематические погрешности, которые могут оставаться незамеченными вследствие их неизменности. Изменения в действии влияющей величины, включение или выключение порождающего ее источника в течение процесса измерения, в большинстве случаев отмечаются по неожиданным изменениям показаний СИ. Это всегда побуждает выявить причины изменений и неоднократно повторить измерения.
Температура окружающей среды может существенно исказить результаты измерения и особенно при неравномерном воздействии на измерительные устройства или на объект измерения. Источники направленного тепла (или холода) имеются практически повсюду.
Это радиаторы центрального отопления, трубы с горячей водой, окна-источники потока холодного воздуха зимой; расположенная рядом аппаратура, потребляющая значительную энергию. Ряд СИ изменяет свои показания при одностороннем незначительном нагреве во много раз больше, чем при равностороннем нагреве. Э.д.с. нормального элемента существенно изменяется даже при незначительной разности температур двух его сообщающихся сосудов. Влияние на работу СИ может оказывать и неравномерность температурного поля помещения. Для точных измерений и поверочных работ часто выделяют сухие подвальные помещения, в которых температуру удается в разные времена года поддерживать постоянной или с очень небольшими колебаниями (в пределах одного градуса). Однако часто в таких помещениях при большой устойчивости температуры на одном уровне разность температур у пола и на высоте человеческого роста может достигать несколько градусов. Следовательно, разные части относительно высокого СИ могут иметь различную температуру, что в течение длительного времени может оставаться незамеченным.
Нередко тепло может быть причиной ошибочных измерений, так как тело, принесенное в помещение с другой температурой, не сразу принимает температуру окружающего воздуха. При включении измерительного прибора различные детали конструкции нагреваются с разной скоростью в зависимости от потребляемой электроэнергии и массы. Со временем за счет явлений излучения, конвекции происходит перераспределения тепла и внутри прибора устанавливается стационарный тепловой режим . Калибровка прибора обычно осуществляется в стационарном режиме. Однако если начать
46
производить измерения до установления теплового режима, можно получить достаточно большую систематическую погрешность.
Виды магнитных полей очень разнообразны - от постоянного магнитного поля Земли до переменного магнитного поля, создаваемого близко расположенными электрическими установками и проводами. Влияние магнитного поля на показание прибора зависит от принципа его действия, конструкции и напряженности магнитного поля. Особенно часто остаются незамеченными магнитные поля создаваемые проводами скрытой проводки, провода цилиндрических реостатов, маломощных трансформаторов. Создают электромагнитные поля и измерительные приборы, которые могут оказывать взаимное влияние.
Магнитные поля могут оказывать влияние на показания любого измерительного прибора, имеющего подвижные части из магнитного материала (сталь, никель). Это влияние может выразиться в намагничивании этих частей и отклонении их от нормального положения под действием постороннего магнитного поля, например магнитного поля Земли. Особенно заметное действие оказывают на показания СИ высокочастотные магнитные поля. Но даже на частоте 50 Гц при точных измерениях бывает нелегко освободиться от влияния посторонних полей, а так же вредного воздействия одних частей измерительных цепей на другие.
Электрические поля так же могут оказывать существенное влияние на показания СИ. При близком расположении отдельных частей цепи, приборов или проводов, между ними возникает емкостная связь, которая может исказить результаты измерений.
2.1.5.Субъективные систематические погрешности.
Эти погрешности, как правило, являются следствием индивидуальных свойств человека, обусловленных свойствами его организма или укоренившимися неправильными навыками. Практика показывает, что у опытного экспериментатора может быть значительная субъективная систематическая погрешность, связанная с его привычками. Эта систематическая погрешность устойчиво повторяется при повторении измерений, при малом случайном разбросе результатов. Наоборот, у малоопытного экспериментатора субъективная систематическая погрешность может отсутствовать, однако разброс результатов от опыта к опыту может быть существенным.
В возникновении субъективных погрешностей большую роль играет также скорость реакции на полученный сигнал. У каждых лиц она различна, но в течение более или менее продолжительного времени достаточно устойчива.
47
2.1.6.Характер проявления систематических погрешностей.
По характеру проявлений систематические погрешности подразделяют на постоянные и переменные. Переменные погрешности в свою очередь подразделяют на
прогрессивные, периодически изменяющиеся по сложному закону. Постоянные систематические погрешности характеризуются тем, что в течение всего времени измерений их значение и знак остаются неизменными. Тот факт, что такие погрешности в течение длительного времени остаются неизменными, является весьма важным при их учете. Постоянные систематические погрешности имеют большинство мер, катушек индуктивностей, магазинов сопротивлений, погрешности градуировки шкал приборов, смещение установки нуля стрелочных приборов и т.п.
Прогрессивные погрешности – погрешности, которые в процессе измерений постепенно возрастают или убывают. Одной из причин появления таких погрешностей является, например, разряд питающего аккумулятора или батареи в процессе измерений.
Периодические погрешности, периодически изменяющие свое значение и знак, возникают при применении средств измерений с круговой шкалой, стрелка которых при измерениях совершает несколько оборотов, например индикаторы часового типа, органы управления частотой измерительного генератора. Систематические погрешности периодического типа возникают в таких случаях, когда ось вращения стрелки не совпадает с центром окружности шкалы.
Погрешности, изменяющиеся по сложному закону, могут быть выражены в виде формулы или графика. Такого типа погрешности возникают при изменении по определенному закону, какого либо влияющего фактора, например изменения температуры.
2.1.7. Способы исключения и учета систематических погрешностей.
Способы исключения и учета систематических погрешностей можно разделить на четыре основные группы:
•устранение источников погрешностей до начала измерений;
•исключение погрешностей в процессе измерения способами замещения, компенсации погрешности по знаку, противопоставления, симметричных наблюдений;
•внесение поправок в результат измерения;
•оценка границ, не исключенных систематических погрешностей.
Устранение источников погрешностей до начала измерений – наиболее рациональный способ исключения систематических погрешностей. Он освобождает экспериментатора от необходимости вычислять результат с учетом поправок, устранять погрешности в процессе измерений и т.п. Под устранением источника погрешностей понимается как его
48
непосредственное удаление (например, удаление источника тепла), так и защиту СИ и измеряемого объекта от влияния этих источников. Источники инструментальной погрешности, присущие конкретному экземпляру СИ, могут быть устранены путем его калибровки или ремонта. Источники погрешностей, связанные с неудачным взаимным расположением СИ могут быть устранены перед началом измерений.
Устранение влияния температурных колебаний и, как следствие, температурной погрешности может быть достигнуто термостатированием как помещений в целом, так и отдельных СИ или их частей. В настоящее время термостатирование часто заменяется кондиционированием воздуха. При кондиционировании поддерживается на требуемом уровне не только температура, но и влажность. Однако результат от этих мероприятий оказывается эффективным при равномерном распределении тепла, так как неравномерное распределение тепла по объему СИ может вызывать погрешности. Следует так же обращать внимание на те СИ, которые имеют внутри корпуса достаточно мощные источники тепла. Такие устройства перед началом измерений обычно некоторое время прогревают.
Устранение влияния магнитных полей обычно осуществляется методом экранирования. Одним из источников погрешностей является магнитное поле Земли. Напряженность магнитного поля Земли невелика, поэтому опасность его воздействия возникает только при применении приборов, отличающихся повышенной чувствительностью. Единственным средством защиты приборов в этом случае является устройство замкнутых экранов из магнито - мягких материалов. Магнитные силовые линии должны огибать экранируемое пространство. Эффективное экранирование достигается применением пермаллоя с большой магнитной проницаемостью и малой коэрцитивной силой. Применение магнитного экрана даже из пермаллоя может вызывать и нежелательные явления, поскольку приводит к изменению конфигурации магнитного поля внутри экрана и влиять на показания СИ.
Несколько легче осуществляется экранирование от внешних высокочастотных электромагнитных полей. В этом случае целесообразно применение материалов, обладающих большой электропроводностью. Эффект достигается за счет вихревых токов и создаваемых ими встречных электромагнитных полей.
Устранение влияния вибраций и сотрясений осуществляется путем амортизации СИ, для чего используют самые разные поглотители колебаний. Тип поглотителей, а также эластичные подвесы, пружины подбираются в зависимости от частоты колебаний и чувствительности к этим влияниям конкретных СИ.
Исключение систематических погрешностей в процессе измерений обычно не связано с применением, каких либо приспособлений. Как правило, устранение систематических
49
погрешностей в этом случае связано с применением тех или иных способов измерений и приемов. Исключению таким путем в основном поддаются инструментальные погрешности, погрешности от взаимной установки и погрешности от внешних влияний.
Одним из наиболее распространенных способов исключения систематических погрешностей является способ замещения. Он заключается в том, что измеряемый объект заменяется известной мерой, находящейся в тех же условиях, в какой находился он сам.
Применительно к измерению электрических параметров – сопротивления, индуктивности, ёмкости, прием замещения заключается в следующем.
Объект, электрическое сопротивление, индуктивность или ёмкость которого необходимо измерить, включают в измерительную цепь. В большинстве случаев применяю нулевые методы измерений (мостовые, компенсационные и др.) при которых осуществляется электрическое уравновешивание цепи. После уравновешивания вместо измеряемого объекта, не изменяя схемы, включают многозначную меру: магазин сопротивления, ёмкости, индуктивности. Изменяя их значение, добиваются восстановления равновесия цепи. Способ замещения позволяет исключить влияние остаточной неуравновешенности мостовых цепей, влияние на цепь магнитных и электрических полей, взаимные влияния отдельных элементов цепи, утечек и других паразитных явлений.
Способ компенсации погрешности по знаку заключается в том, что измерение проводят дважды так, чтобы известная по природе, но неизвестная по размеру погрешность входила в результаты измерений с противоположными знаками. Погрешность исключается при вычислении среднего значения. В алгебраической форме это можно выразить
следующим |
образом. |
Пусть |
х1 , х2 − результаты |
двух измерений; - |
систематическая |
||||||
погрешность, природа которой известна, но неизвестна её величина; |
хД - значение |
||||||||||
измеряемой |
величины, |
свободное от данной |
составляющей погрешности. Тогда |
||||||||
х1 = хД + ; х2 = хД + . |
|
|
|
|
|||||||
Среднее значение равно: |
|
|
|
|
|
|
|
|
|||
|
х = |
х + х |
2 |
= |
(хД + )+ (хД − |
) |
= хД . |
|
|||
|
|
1 |
|
|
|
|
|
||||
|
|
|
2 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
С целью повышения точности результата можно провести и большее чем два, количество измерений, однако их число обязательно должно быть четным. В этом случае все погрешности с положительным знаком, уравновешивались точно таким же количеством
50
погрешностей с отрицательным знаком. Данный способ может быть рекомендован для исключения таких погрешностей, источники которых имеют направленное действие. Данный способ широко используется для исключения погрешности связанной с влиянием магнитного поля Земли. Первое измерение можно проводить, когда СИ находится в произвольном положении. Перед проведением второго измерения СИ поворачивают в горизонтальной плоскости на 1800 . Если в первом случае магнитное поле Земли, складываясь магнитным полем прибора, вызывает погрешность с положительным знаком, то при повороте на 1800 магнитное поле Земли будет оказывать противоположное действие и вызовет погрешность равную по величине, но противоположного знак. Применение данного метода для компенсации влияния магнитных полей искусственного происхождения ограничено, поскольку магнитные поля такого типа обычно неравномерны в пространстве.
Пользуясь способом компенсации систематической погрешности по знаку, можно исключить погрешности, вызванные гистерезисом в магнитных материалах.
Внесение известных поправок позволяет путем вычислений исправить результат измерения. Наиболее распространено алгебраическое сложение результата измерения и поправки с учетом её знака. Поправка по числовому значению равна систематической погрешности и противоположна ей по знаку.
Вдругих случаях погрешность исключают путем умножения результата измерения на поправочный множитель, который может быть несколько больше или меньше единицы. Можно рассчитывать на высокую точность исправленного результата, если поправка мала по сравнению измеренной величиной или поправочный множитель близок к единице.
Имеются некоторые тонкости вычислений при использовании поправочных множителей. Как отмечалось, поправочный множитель близок к единице. Величина 1,1 тем не менее слишком велика, так как единица в десятичном знаке составляет 10 %, а такие погрешности слишком велики. Поэтому речь обычно идет о поправочных множителях порядка 1,01; 1,02; 1,03 и т.д.
Вряде случаев исключение систематических погрешностей оказывается практически невозможным. Это относится к методам измерений, систематические погрешности которых плохо изучены. Ограничено применение поправок в показания счетчиков электроэнергии. Угловая скорость диска в каждый данный момент пропорциональна потребляемой мощности. Однако в действительности она не строго пропорциональна потребляемой мощности, отчего возникают систематические погрешности, зависящие от мощности. Использовать поправки можно лишь в том случае, если потребляемая мощность постоянна в течение всего процесса измерения. Поскольку этого не бывает на практике, приходится ограничиваться оценкой возможных границ систематических погрешностей.
51
2.2. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ.
2.2.1. Определение случайных погрешностей.
При проведении повторных измерений одной и той же не изменяющейся величины даже при одинаковых условиях, часто получаются отличающиеся друг от друга результаты. Различие результатов отдельных измерений свидетельствует о наличии случайной погрешности. Случайная погрешность возникает при одновременном воздействии нескольких факторов. Каждый фактор может осуществлять достаточно малое влияние на результат наблюдений, но их суммарное воздействие может оказаться достаточно сильным. Если влияющие факторы не имеют закономерной связи между собой, их влияние на результат измерения носит случайный характер. Такой характер воздействия на результат измерения приводит к тому, что заметные расхождения в результатах отдельных измерений, проявляются без закономерной связи с предыдущими и последующими результатами. Это и дает основание говорить о случайных погрешностях. Следует отметить, что случайные погрешности проявляются при использовании достаточно точных приборов и речь идет о весьма малых отклонениях отдельных результатов измерений.
Изучение случайных погрешностей осуществляется на основе теории вероятностей и математической статистики. Развитие метрологии показало, что математический аппарат теории вероятностей и математической статистики соответствует задаче изучения случайных погрешностей и при его корректном применении теоретические результаты хорошо согласуется с опытными данными. Причинами расхождений результатов повторных измерений могут оказаться случайные изменения самой измеряемой величины. Выяснить, что является причиной расхождения результатов отдельных измерений иногда достаточно сложно.
2.2.2. Математические модели случайной погрешности.
При наличии случайных погрешностей результат отдельного измерения Хi может отличаться от истинного значения Х измеряемой величины: X i − X = X . Эту разность называют случайной погрешностью отдельного измерения. Истинное значение Х нам неизвестно, однако математическая статистика позволяет на основе результатов многократных измерений вычислить так называемое «действительное» значение, которое может с достаточной для практики степени точности заменить истинное значение при определении погрешности Х.
52
Универсальным способом описания поведения случайных погрешностей является функция распределения F(x), определяющая вероятность того, что случайная величина Х в результате измерений примет значение меньшее х, т.е. F(x) = P (X< x). Геометрически это можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Непрерывную случайную величину можно также задать другой функцией, которую называют плотностью распределения, или плотностью вероятности. Плотностью распределения вероятностей непрерывной случайной величины называют функцию f ( x ) – первую производную от функции распределения F(x) По своему смыслу плотность вероятности равна отношению вероятности попадания случайной величины внутрь
интервала |
Х к длине этого интервала в предположении, что последняя стремится к нулю: |
|
|
f ( x ) = F ' (x). |
( 2.1) |
Применительно к рассматриваемой задаче функция плотности распределения имеет отношение, как результатам отдельных измерений, так и к их погрешностям. Дело в том, что при наличии случайной погрешности принята, так называемая, интервальная оценка, как результата измерения, так и погрешности. В этом случае определяется наиболее вероятное значение измеряемой величины и некий интервал (плюс-минус) в котором может оказаться отдельный результат измерения с определенной вероятностью. Определение этой вероятности может осуществляться на основе известной теоремы - «Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, в), равна определенному интегралу от плотности распределения вероятности, взятому в пределах от а до б»:
P (a < X < b)= ∫b |
f (x)dx . |
(2.2) |
a |
|
|
Конкретный вид функции плотности вероятности f (x) зависит от свойств применяемого средства измерения. Достаточно часто для оценки случайной погрешности измерения применяется нормальный закон распределения (закон Гаусса):
f (x)= |
|
1 |
e−(x−a)2 / 2σ2 |
(2.3). |
|
σ |
2π |
||||
|
|
|
Из (2.3) видно, что нормальное распределение определяется двумя параметрами: а и σ. Вероятностный смысл этих величин таков: а – величина математического ожидания, σ – среднее квадратическое отклонение нормального распределения.
Математическое ожидание определяется через интеграл:

53
M (X )=+∞∫x f (x)dx |
(2.4). |
−∞ |
|
Среднее квадратическое отклонение определяется через дисперсию непрерывной случайной величины. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [cd ] , то
D(X )= ∫d [x − M (X )]2 f (x)dx |
(2.4). |
c |
|
Среднее квадратическое отклонение, входящее в формулу (2.3), определяется равенством
σ(X )= D(X ) |
(2.5). |
Применив формулу 2.3. к описанию плотности вероятности погрешности измерений, получим:
p( X ) = |
1 |
|
e−( X )2 2σ 2 |
|
|
|
|
||
|
σ 2π |
(2.6), |
|
|
|
|
|
|
|
где p( X) – плотность |
вероятности случайной погрешности |
X = X i − X ; |
||
σ – среднее квадратическое отклонение – параметр, характеризующий степень случайного разброса результатов отдельных наблюдений относительно истинного значения Х.
Величину среднего квадратического отклонения погрешности измерения определяют из соотношения:
|
n |
|
n |
|
|
σ = |
∑(X i − X )2 |
= |
∑( X i )2 |
|
|
1 |
1 |
(2.7), |
|||
n |
n |
||||
|
|
|
в котором Xi – результат отдельного измерения, n – количество измерений, Х – истинное значение измеряемой величины.
Графики функции, описываемых выражением (2.6), показаны на рис. 2.1.а для трёх значений σ. По горизонтальной оси отложена нормированная величина Х/σ, т.е величина погрешности отнесенная к среднеквадратическому отклонению. Функция (2.6) графически
54
изображается колоколообразной кривой, симметричной относительно ординат, асимптотически приближающейся к оси абсцисс. Максимум этой кривой получается в точке
Х=0, а величина этого максимума p( X ) = 1 σ
σ  2π . Как видно из рис. 2. 1.а, чем меньше σ,
2π . Как видно из рис. 2. 1.а, чем меньше σ,
тем уже кривая и, следовательно, реже встречаются большие отклонения, т.е. тем точнее выполняются измерения.
1 |
|
P( x) |
|
|
P( x) |
0,8
|
0,4 |
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
-ε |
ε |
|
x/σ |
|
|
|
|
||
|
|
|
|
-ε |
x1 |
x2 +ε |
+ x |
||
-3 -2 -1 |
0 |
1 2 |
3 |
- x |
|||||
|
|||||||||
а) |
б) |
|
Рис. 2.1
Вероятность появления погрешности в пределах между Х1 и Х2 определяется площадью заштрихованного участка на рис. 2.1.б, т.е. определённым интегралом от функции p( Х):
|
|
|
x2 |
|
1 |
− |
1 |
|
X 2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
p( X ≤ X ≤ X |
2 |
) = |
∫x |
|
e |
2 |
|
σ d( X) |
|
||
|
|
|
|
|
|||||||
1 |
|
σ |
2π |
|
|
|
|
|
(2.8). |
||
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
Значения интеграла вычислены для различных пределов и сведены в таблицы.
Интеграл, вычисленный для пределов X1= – ∞ и X2= +∞, равен единице, т. е. вероятность появления случайной погрешности в интервале от –∞ до +∞ равна единице. При проведении
расчетов часто величины |
Х1 и Х2 принимают равными по величине и |

55
противоположными по знаку, что позволяет вместо них ввести более удобный символ ε, и
интервал, в котором оценивается вероятность обозначать ±ε . Данный интервал на рис.2.1а
располагается симметрично относительно вертикальной оси.
Величину ε удобно связать со средним квадратическим отклонением с помощью безразмерного коэффициента k, т.е. принять ε = kσ . Величину ±ε принято называть
доверительным интервалом, а вероятность Р с которой погрешность укладывается в данный интервал, доверительной вероятностью. Результат измерения можно представить в виде А ±ε ; Р.
Необходимые расчеты можно выполнить используя функцию Лапласа, значения которой табулированы и имеются в математических справочниках. Для этого формулу 2.8 следует преобразовать, введя новую переменную k = ε/σ:
p (−x ≤ k ≤ x) =2 Ф(x)= |
2 |
∫x e− k 2 / 2 dt |
(2.9). |
|
2π |
||||
|
0 |
|
При выводе формулы (2.9) учитывалась симметричность функции нормального распределения относительно вертикальной оси, что позволил нижний предел интегрирования установить равным нулю и ввести коэффициент 2 перед интегралом.
Таблица 2.1. Значения интеграла вероятностей |
|
|
|||||
х |
2Ф(х) |
х |
2Ф(х) |
х |
2Ф(х) |
х |
2Ф(х) |
0,00 |
0,00000 |
0,70 |
0,51607 |
1,40 |
0,83849 |
2,25 |
0,97555 |
0,10 |
0,07966 |
0,80 |
0,57629 |
1,50 |
0,86639 |
2,50 |
0,98758 |
0,20 |
0,15852 |
0,90 |
0,63188 |
1,60 |
0,89040 |
2,75 |
0,99404 |
0,30 |
0,23585 |
1,00 |
0,68269 |
1,70 |
0,91087 |
3,00 |
0,99730 |
0,40 |
0,31084 |
1,10 |
0,72867 |
1,80 |
0,92814 |
3,30 |
0,99903 |
0,50 |
0,38292 |
1,20 |
0,76986 |
1,90 |
0,94257 |
3,50 |
0,99953 |
0,60 |
0,45149 |
1,30 |
0,80640 |
2,00 |
0,95450 |
4,00 |
0,99994 |
Из таблицы 2.1, следует, что значение интеграла в (2.9):
P(−σ ≤ X ≤ σ) = 0,68269; P(−3σ ≤ X ≤ 3σ) = 0,99730 |
(2.10). |
Таким образом, с вероятностью 0,68269 случайные погрешности измерения не выходят за пределы ±σ. С вероятностью 0,99730 случайная погрешность находится в пределах ±3σ. Это соотношение называется законом трёх сигм. Округлив 0,99730 до 0,997 можно сказать, что вероятно только 3 измерения из 1000 могут дать погрешность превышающую ±3σ.
56
Случайные величины и их вероятности, к которым относятся результаты отдельных наблюдений, можно изучать статистическим методом, проводя для этой цели большое количество измерений. Определение, таким образом, законов распределения случайных величин, достаточно трудоёмкий процесс. Поэтому обычно на основании теоретических соображений прогнозируется вид функции распределения случайных величин, а далее на основе сравнительно небольшого ряда измерений, она определяется количественно. Хотя отдельные факторы, влияющие на случайную погрешность измерения, могут иметь различные функции распределения вероятностей, результирующая функция будет определяться законом Гаусса, вследствие явления «нормализации» Для большого числа встречающихся на практике измерений случайная погрешность определяется суммой большого количества влияющих факторов поэтому с большой вероятностью можно ожидать наличия нормального закона распределения погрешностей.
Как отмечалось ранее при наличии случайных погрешностей результат отдельного
измерения Хi |
может |
отличаться от |
истинного |
значения |
Х измеряемой |
величины: |
X i − X = |
X . |
Эту разность |
называют |
случайной |
погрешностью |
отдельного |
измерения. Истинное значение Х нам неизвестно. Однако, проведя большое количество наблюдений исследуемой величины Х, можно выявить следующие статистические закономерности, характерные для нормального распределения.
Если проводить серию измерений исследуемой величины и определить среднее значение, то положительные и отрицательные отклонения отдельных результатов наблюдений от среднего значения имеют приблизительно равную вероятность. Это является причиной того, что имеется равная вероятность (частота) отклонения результатов наблюдений от истинного значения величины в сторону уменьшения и увеличения, в том случае, когда систематическая погрешность равна нулю. Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине. При вычислении среднего арифметического большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются. Другая закономерность заключается в том, что вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности появления малых отклонений.
Эти статистические закономерности справедливы лишь при многократном повторении измерений. После обработки результатов измерений, получается не абсолютно достоверный, а наиболее вероятный результат и этим результатом будет среднее

57
арифметическое ряда измерений:
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
X |
|
+ X |
|
+ X |
|
+K+ X |
|
|
∑X i |
|
|
X = |
1 |
2 |
3 |
n |
= |
i=1 |
(2.11) |
||||||
|
|
|
|
||||||||||
|
|
|
|
n |
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
где n – число измерений.
Для определения случайной погрешности X i = Ai − X необходимо знать истинное значение измеряемой величины, которое неизвестно. Однако среднее арифметическое является наиболее достоверным значением, которое можно приписать измеряемой величине. Поэтому можно использовать среднее арифметическое в качестве её оценки. В этом случае отклонения результатов отдельных измерений от среднего арифметического равны
X i − X =Ui .
В теории погрешностей показывается, что среднее арифметическое X удовлетворяет следующим условиям:
•алгебраическая сумма случайных отклонений отдельных измерений от среднего
арифметического при достаточно большом количестве измерений равна нулю:
n |
|
n |
∑(X i − |
|
) = ∑Ui = 0 ; |
X |
||
1 |
1 |
|
•сумма квадратов отклонений от среднего арифметического
n |
n |
|
||
∑(X i − |
|
)2 |
= ∑Ui2 |
|
X |
имеет наименьшее значение. |
|||
1 |
|
|
1 |
|
Представленные выше формулы выведены из условия, что число наблюдений n → ∞. На практике число измерений конечно, и это приводит к необходимости введения поправок,
роль которых снижается при увеличении числа измерений, так как X и Х всё больше сближаются и в пределе становятся равными. Это означает, что все выводы, относящиеся к случайным погрешностям Х (в частности закон Гаусса), можно применить и к отклонениям от среднего арифметического. Если вместо Х ввести X и вместо Xi ввести Ui, то, как доказывается в математической статистике, формула (2.5) принимает вид:
|
n |
|
n |
2 |
||
|
∑Ui2 |
|
∑(X i − |
|
) |
|
|
X |
|||||
s = |
1 |
= |
1 |
|
|
|
n −1 |
n −1 |
|
||||
|
|
|
||||
58
При приближенных вычислениях, когда вместо Х используется U, а вместо Х берётся
X , среднее квадратическое отклонение обозначают обычно через s вместо σ.
Данным соотношением можно пользоваться при n ≥ 10. Из выражения 2.12. следует, что проведя в 100 раз больше измерений, можно получить с той же вероятностью результат на один дополнительный десятичный знак более точный. Однако нельзя забывать, что данный результат может быть получен только при обеспечении постоянства и единообразия условий измерений. Чем больше число измерений, тем больше времени необходимо для их проведения и труднее выполнить это условие.
Следует иметь в виду, что в пределе при n → ∞ значение X = X лишь в случае, когда все систематические погрешности исключены из результатов измерений и чувствительность измерительного прибора достаточно велика. Если в условиях практических измерений стократное увеличение числа измерений не всегда целесообразно, то увеличение числа наблюдений в два или четыре раза безусловно заметно повышает точность и надежность результата измерений. Так, теоретически случайная погрешность результата измерения при увеличении числа наблюдений в четыре раза уменьшится приблизительно в два раза, а при увеличении в десять раз - примерно в три раза при одной и той же доверительной вероятности.
На практике широко пользуются понятием максимальной погрешности, под которым понимают закон трёх сигм. Так как на практике число измерений не превышает нескольких десятков, то появление погрешности равной ±3σ , маловероятно. Поэтому погрешность ±3σ
считается максимально возможной случайной погрешностью. Погрешности более ±3σ считаются промахами и при обработке результатов измерений не учитываются.
Как отмечалось среднее арифметическое ряда измерений X является лишь наиболее достоверным значением измеряемой величины. Представляет интерес оценка погрешности определения самого среднего арифметического. Если проводить серии измерений и для каждой серии вычислить среднее арифметическое, то будут получены значения
X 1 , X 2 , X 3 KX n . Эти величины будут отличаться друг от друга и, следовательно, для них
может быть определено среднее квадратическое отклонение от среднего арифметического. Если случайные погрешности результатов отдельных наблюдений подчиняются нормальному распределению, то и погрешности средних значений их повторных рядов подчиняются этому же закону, но уже с другим рассеянием. Рассеяние средних значений меньше, чем рассеяние результатов отдельных наблюдений. В теории вероятностей доказана теорема : « Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в  n раз меньше среднего
n раз меньше среднего

59
квадратического отклонения каждой из величин». На основании этой теоремы получаем следующее выражение среднего квадратического отклонения для среднего арифметического значения.
|
|
|
|
|
n |
|
s |
|
= |
s |
= |
∑Ui2 |
|
|
1 |
(2.13), |
||||
X |
n |
n(n −1) |
||||
|
|
|
|
|
где sX – средняя квадратическая погрешность среднего арифметического из ряда измерений; s – средняя квадратическая погрешность отдельного измерения; n – число измерений в серии. Из данного выражения видно, что увеличение числа повторных измерений n приводит к уменьшению средней квадратической погрешности результата измерений в  n раз.
n раз.
На практике (особенно при малом значении n) необходимо оценить надёжность и точность полученных результатов. Для этой цели пользуются доверительной вероятностью и доверительным интервалом. Под доверительной вероятностью понимают вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называется доверительным интервалом, а характеризующую её вероятность p – доверительной вероятностью.
При гауссовском законе распределения по таблице интеграла вероятности можно определить значения доверительных интервалов. При увеличении доверительных интервалов значение доверительной вероятности возрастает, стремясь к своему пределу, равному единице. Как уже отмечалось, для интервала ±3σ значение вероятности составляет 0,9973. С введением новых понятий это можно интерпретировать так, для доверительного интервала от – 3σ до +3σ доверительная вероятность равна 0, 9973. Для оценки погрешности отдельного измерения пользуются также вероятной погрешностью ρ, под которой понимают величину, характерную тем, что все случайные погрешности данного ряда из n измерений она делит на две равные части; в одной находятся n 2 случайных погрешностей,
2 случайных погрешностей,
превышающих ρ, а в другой n 2 случайных погрешностей, меньших ρ. Иначе говоря,
2 случайных погрешностей, меньших ρ. Иначе говоря,
вероятность того, что некоторая случайная погрешность лежит в пределах от –ρ до +ρ, должна равняться 0,5. Вероятная погрешность для гауссовского закона равна:
|
|
|
|
|
n |
|
ρ = |
2 |
s = |
2 |
|
∑Ui2 |
|
1 |
(2.14) |
|||||
3 |
3 |
|
n −1 |
|||
|
|
|
|
|||
60
Определение доверительных интервалов с использованием соотношения (2.8) справедливо лишь при числе измерений n ≥ 17 . На практике приходится оценивать погрешности по результатам сравнительно небольшого количества измерений. Применение формулы (2.8) в данном случае даст заниженное значение доверительного интервала, т. е. оценка точности измерения оказывается неоправданно завышенной. В этом случае уточнить доверительный интервал можно с помощью коэффициентов Стьюдента tn, которые зависят от задаваемой доверительной вероятности p и числа измерений n.
Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат можно записать так:
X = X ± tn S X .
Величина tn определяется распределением Стьюдента (псевдоним математика В.С.
Госсета). Распределением Стьюдента при любом числе измерений при n ≥ 2 называется распределение с плотностью вероятности р(t,n) :
S(t, n)= |
1 |
|
|
Г(n / 2) |
|
|
|
|
t |
2 |
−n / 2 |
|
|
|
|
1 |
+ |
|
|
||||
|
|
|
|
|
|
|
|||||
π(n |
−1) |
|
Г((n −1)/ |
|
|
|
|
|
|||
|
|
2) |
|
|
n −1 |
||||||
Где n – число измерений; Г- гамма-функция;
t = n X − X sX
нормированное значение случайной величины.
|
t(n,р) |
(I) р(н) |
|
0,4 |
|
|
|
|
(II) n=5 |
0,3 |
|
(III) n=3 |
|
0,2 |
0,1
-6 -4 -2 0 2 4 6
(2.15),
(2.16),
t

61
Рис.2.2.
Графически плотность распределения вероятности по Стьюденту представлена на рис.2.2. Для сравнения на рис. 2.2. (кривая I) изображен график нормального распределения вероятностей для n ≥ 17 . Графики распределения Стьюдента для количества измерений n =5 и 3 представлены кривыми (II) и (III). Как видно из рис. 2.2., по форме графики распределения Стьюдента напоминают график нормального распределения. Основное отличие заключается в том, что они характеризуют большее рассеяние погрешностей результатов измерений. Так для графика (I) вероятность практически равна нулю при t =3, что соответствует «закону трех сигм», в то время как для n =5 при t =4, а для n =3 при t =6. При увеличении количества измерений до n ≥ 17 кривая распределения Стьюдента переходит в кривую нормального распределения.
Значения коэффициентов Стьюдента tn, необходимых при выражении результата измерения по формуле X = X ± tn S X , приводятся обычно в таблицах. Их можно найти в
справочниках по математике. Эти таблицы содержат коэффициенты Стьюдента для двух изменяющихся параметров: числа измерений n и вероятности p. В сокращенном виде значения коэффициентов Стьюдента представлены в таблице 2.2.
Так, например, при доверительной вероятности 0,98 и n = 10 коэффициент Стьюдента tn= 2,82 , а для n = 12 величина tn= 2,72. Как видно из приведённых цифр, увеличение числа
измерений приводит к уменьшению коэффициента Стьюдента. |
|
|
|||||||
|
Таблица 2.2. |
|
|
|
|
|
|
|
|
n |
При доверительной вероятности Р |
n |
При доверительной вероятности Р |
||||||
|
0,90 |
0,95 |
0,98 |
0,99 |
|
0,90 |
0,95 |
0,98 |
0,99 |
2 |
6,31 |
12,71 |
31,82 |
63,68 |
11 |
1,81 |
2,23 |
2,76 |
3,17 |
3 |
2,92 |
4,30 |
6,97 |
9,93 |
12 |
1,80 |
2,20 |
2,72 |
3,11 |
4 |
2,35 |
3,18 |
4,54 |
5,84 |
13 |
1,78 |
2,18 |
2,68 |
3,06 |
5 |
2,13 |
2,78 |
3,75 |
4,60 |
14 |
1,77 |
2,16 |
2,65 |
3,01 |
6 |
2,02 |
2,57 |
3,37 |
4,06 |
15 |
1,76 |
2,15 |
2,62 |
2,98 |
7 |
1,94 |
2,45 |
3,14 |
3,71 |
16 |
1, 75 |
2,13 |
2,60 |
2,95 |
8 |
1,9 |
2,37 |
3,00 |
3,50 |
17 |
1, 75 |
2,12 |
2,58 |
2,92 |
9 |
1,86 |
2,31 |
2,90 |
3,36 |
18 |
1, 74 |
2,11 |
2,57 |
2,90 |
10 |
1,83 |
2,26 |
2,82 |
3,25 |
19 |
1, 73 |
2,10 |
2,55 |
2,88 |
62
Кроме нормального закона распределения случайных погрешностей в метрологической практике оказывается целесообразным использование и других законов. Одним из них является равномерный закон.
Равномерный закон.
Равномерному закону подчиняются погрешности возникающие при квантовании и дискретизации измерительного сигнала, погрешности связанные с трением в опорах стрелочного измерительного прибора, так называемые явления гистерезиса и др.
В радиотехнике и связи, погрешности преобразования сигналов, связанные с квантованием обычно называют шумами квантования. Такой термин «прижился» потому, что при квантовании звукового сигнала, искажения связанные с квантованием воспринимаются слуховым аппаратом как шум. В измерительной технике в цифровых СИ так же применяется квантование. Суть искажений остается той же, поэтому воспользуемся хорошо известными в технике связи соотношениями, однако вместо термина шум квантования будем использовать термин случайная погрешность. Для удобства рассмотрения вопроса на рис.2.3. представлена амплитудная характеристика устройства квантования (рис. 2.3а) и зависимость погрешности квантования от величины измерительного сигнала (рис. 2.3б).
uКВ |
|
а) |
h |
|
|
c |
uвх |
|
h |
|
2 |
h |
|
в) |
uвх |
d |
|
Рис.2.3.
На рис. 2.3а представлена линейная характеристика квантования (характерная для цифровых измерительных приборов) с постоянным шагом h и соответствующей погрешностью

63
квантования, график которой представлен на рис. 2.3.б. Погрешность квантования равна нулю при значениях сигнала uвх, которые соответствуют точкам пересечения ступенчатой характеристики квантования и идеальной линейной характеристикой (рис. 2.3.а). Одна из таких точек показана на рис. 2.3. с помощью штрихпунктирной линией c-d. Поскольку входной измерительный сигнал (uвх) с равной вероятностью может занимать любые уровни при достаточно большом числе уровней квантования можно считать, что погрешность квантования имеет размах h и равномерное распределение плотности вероятности:
p ( )= 1/ h , |
|
|
|
|
≤ h / 2 , |
||
|
|
||||||
p ( )= 0, |
|
|
|
|
|
|
> h / 2 . |
|
|
|
|
|
|||
Тогда дисперсия случайной погрешности равна:
D = +h∫/ 2 |
2 p( )d = h2 / 12. |
−h / 2 |
|
Соответственно среднее квадратическое отклонение равно:
|
|
|
|
σ = |
D = |
|
h |
|
= |
П |
|
||
|
|
|
|
12 |
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
В последнем выражении |
П -предельная погрешность, равная h / 2. |
||||||||||||
|
Плотность вероятности для равномерного закона распределения погрешностей можно |
||||||||||||
записать: |
|
|
|
|
|
|
|
|
|
|
|
||
p ( |
c |
при |
|
1 < |
< |
2 |
|
|
|
|
|||
X )= |
при |
|
< |
|
и |
> 2 |
, |
|
|||||
|
0 |
|
1 |
|
|||||||||
где |
с = |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
− |
1 |
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Графически зависимость представлена на рис.2.4.
p( X)
σ= П 
 3 с
3 с
64
Треугольный закон распределения погрешностей.
Треугольный закон распределения погрешностей встречается у цифровых приборов. Можно показать, что треугольный закон является композицией двух равномерных законов с одинаковой дисперсией.
График треугольного закона распределения плотности вероятностей случайных погрешностей показан на рис. 2.5.
p( X)
1/ П
− П |
|
X |
0 |
П |
|
|
Рис.2.5 |
|
Аналитически плотность вероятности будет выражаться формулами.
65
|
Х |
|
+ |
|
1 |
|
|
при |
− П ≤ |
Х ≤ 0 , |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|||||||||
|
|
П |
Х |
|
|
П |
1 |
|
|
|
|
||||
p( Х)= − |
|
|
+ |
|
при |
0 ≤ |
Х ≤ |
П , |
|||||||
|
|
2 |
|
|
|||||||||||
|
|
|
|
П |
|
|
|
П |
|
|
|
||||
|
|
|
при |
|
|
|
Х < − |
П ; |
Х > |
П . |
|||||
0 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Треугольный закон распределения плотности вероятностей погрешностей характерен для цифровых приборов, в которых применяется метод дискретного счета. В качестве примера на рис. 2.6 иллюстрируется принцип цифрового метода измерения временного интервала этим методом. Измеряемый интервал представляется импульсом прямоугольной формы, длительность которого- Тх , необходимо измерить. Для измерения временного интервала формируются вспомогательные короткие счетные импульсы, следующие с периодом Тсч . Период следования импульсов калиброван ( в приборах они формируются из синусоидального сигнала кварцованного генератора) и, следовательно они являются мерой. Измерение осуществляется методом сравнения Тх с мерой Тсч. Метод называется методом дискретного счета, потому, что производится счет количества импульсов, приходящихся на измеряемый временной интервал, называемый иногда «временными воротами». Для этой цели используют схему, работающую по принципу электронного ключа: при подаче на её вход управляющего сигнала (прямоугольного импульса длительностью Тизм ) счетные импульсы поступают на её выход и далее на электронный счетчик.
t1 |
|
|
|
|
|
|
|
Тх |
|
|
|
|
|
|
|
|
|
|
t2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Тсч |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рис.2.6
Как видно из рис.2.6, количество импульсов N, которое будет зафиксировано счетчиком, равно шести и результат измерения Тизм = N Тсч = 6 Тсч . Результат завышен на единицу счета, поскольку количество полных интервалов, приходящихся на временные ворота равно 5. Так
66
произошло потому, что прибор считает количество импульсов, в то время как надо считать
количество периодов Тсч и учесть «выпавшие» участки – t1 и t2. |
|
|
Таким образом, истинное значение временного интервала Тх = |
(N-1) |
Тсч + t1+ t2, а |
измеренное Тизм = N Тсч . Погрешность измерения Тизм = Тизм - Тх = |
t1+ |
t2. |
Как видно из приведенного примера, составляющие погрешности |
t1 и t2 не связаны друг с |
|
другом. Их величины случайны, поскольку положение фронта и спада импульса, длительность которого измеряется, относительно счетных импульсов, так же случайно. Очевидно, что плотность вероятности каждой из величин t1 и t2 является равномерной.
Как доказывается в теории вероятности, плотность распределения суммы двух независимых величин, называемая композицией, может быть определена с помощью формулы свертки. Расчеты показывают, что композиция представляет в данном случае треугольное распределение, показанное на рис.2.5.
При треугольном распределении среднеквадратическое отклонение можно вычислить по формуле σ = П /  6 , где максимальное значение погрешности. В рассмотренном случае
6 , где максимальное значение погрешности. В рассмотренном случае
σ = Тсч /  6 , так как максимальные значения погрешностей t1 и t2 одинаковы и равны Тсч.
6 , так как максимальные значения погрешностей t1 и t2 одинаковы и равны Тсч.
Закон арксинуса.
При измерении постоянного напряжения вольтметром на вход прибора кроме измеряемого напряжения U Х , может поступать напряжение помехи
вызванной наводками от питающей сети (рис.2.7) .
u
uП
Ux 
0 |
tизм |
|
tизм |
Рис.2.7
67
Если время измерения помехи много меньше периода колебаний, можно считать, что вольтметр измеряет мгновенное значение напряжения, т.е. U Х + иП . Момент включения вольтметра - , случаен по отношению к помехе, поэтому помеху можно считать реализацией случайного процесса - гармонического напряжения со случайной фазой,
равномерно распределенной в пределах ±π . В курсе теории вероятностей показано, что в этих условиях плотность вероятности мгновенного значения помехи описывается законом арксинуса:
p( |
Х)= |
1 |
, |
π uП2 −(Х)2 |
график которого показан на рис. 2.6. В этой формуле: - uП < X< uП .
p( Х)
Х
-uП +uП
Рис. 2.8
Среднее квадратическое отклонение σ =U П /  2 - т.е. равно среднему квадратическому значению гармонической помехи.
2 - т.е. равно среднему квадратическому значению гармонической помехи.
68
2.2.3. Обработка результатов измерений, содержащих случайные погрешности
Методика обработки результатов многократных измерений зависит от свойств погрешностей. Например, если погрешность во время измерений описывается стационарным случайным процессом, то эту стационарность необходимо контролировать. Нестациоарность процесса чаще всего может проявляться в форме изменений математического ожидания – систематической погрешности. Поэтому при обработке результатов необходимо убедиться в отсутствии «ухода» систематической погрешности. Результаты наблюдений не должны содержать грубых погрешностей, которые исключают из расчетов.
Для правильного выбора алгоритма обработки результатов измерений необходимо знать закон распределения погрешностей, который оценивают по экспериментальным результатам. Исходные данные для выбора закона распределения получают из гистограммы. Для ее построения по результатам многократных измерений строят вариационный ряд - располагают результаты в порядке возрастания и выбирают максимальное и минимальное значения измеряемой величины. Далее интервал Хmax разбивают на r интервалов
шириной Xi (i =1,2,....r) и подсчитывают частоты mi , равные числу результатов, лежащих в каждом i-ом интервале, т.е. меньших или равных его правой и больших левой границы.
Отношения
P |
= |
m i |
, |
|
|||
i |
|
n |
|
|
|
|
|
где n −общее число |
наблюдений, называют относительными частотами попадания |
||
результата наблюдений в i −ый интервал. Они представляют собой статистические оценки вероятностей попадания результата измерений в i −ый интервал. Распределение частот по интервалам образует статистическое распределение результатов измерений.
Если разделить частоту попадания результата измерений на длину интервала, то
получим оценки средней плотности распределения в интервале X i :
p |
= |
|
1 |
P |
= |
mi |
. |
|
|
|
|||||
i |
|
|
X i |
i |
|
n X i |
|
|
|
|
|
|
|||
Отложим по горизонтальной оси |
интервалы Xi в порядке возрастания индекса i и на |
||||||
каждом интервале построим прямоугольник с высотой равной pi . Полученный график
называется гистограммой статистического распределения. Площадь всех прямоугольников равна единице:
69
∑pi |
X i = ∑mi = |
1 ∑mi =1. |
|||
r |
r |
|
r |
||
i=1 |
i=1 |
n |
|
n |
i=1 |
При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, т.е. к графику плотности вероятности распределения результатов наблюдений.
Pi
X
X i
Рис.2.8.
При построении гистограммы можно пользоваться следующими рекомендациями:
1.Число r интервалов выбирается в зависимости от числа наблюдений согласно таблице
2.3.
Таблица 2.3. |
|
n |
r |
40-100 |
7-9 |
100-500 |
8-12 |
500-1000 |
10-16 |
1000-10000 |
12-22 |
2.Длины интервалов удобнее выбирать равными.
70
3. Масштабы по осям гистограммы должны быть такими чтобы отношение ее высоты к основанию составляло 5:8.
Пример.
Было выполнено 100 измерений значения напряжения. Результаты наблюдений лежат в диапазоне 9,922-9,954 мВ., т.е. зона разброса результатов измерений составляет 0,032 мВ. Весь диапазон удобно разделить на восемь равных интервалов через 0,004 мВ. В таблице 2.3.
приведены частоты mi , относительные частоты попадания в i − ый интервал- Рi , и плотности pi статистического распределения. Построенная на рис.2.7. гистограмма, соответствует данным таблицы 2.3.
После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все характерные черты статистического распределения, сглаживала бы все случайные отклонения, связанные с недостаточным объемом экспериментальных данных. Определение аналитической функции сводится к выбору таких её параметров, при которых достигается наибольшее соответствие её статистическому распределению результатов измерений.
Таблица 2.4.
i |
Х |
i |
Хi+1 |
m |
P |
|
|
|
|
|
i |
|
pi |
||
|
|
|
мВ |
|
i |
|
|
|
мВ |
|
|
|
|
|
|
1 |
9,922 |
9,926 |
1 |
0,01 |
5 |
||
2 |
9,926 |
9,930 |
5 |
0,05 |
25 |
||
3 |
9,930 |
9,934 |
14 |
0,14 |
70 |
||
4 |
9,934 |
9,936 |
27 |
0,27 |
135 |
||
5 |
9,936 |
9,942 |
24 |
0,24 |
120 |
||
6 |
9,942 |
9,946 |
18 |
0,18 |
90 |
||
7 |
9,946 |
9,950 |
9 |
0,09 |
45 |
||
8 |
9,950 |
8,954 |
2 |
0,02 |
10 |
||
Так, если статистическое распределение, определяемое гистограммой, мы хотим описать кривой нормального распределения плотности вероятности, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсии, вычисленной по экспериментальным данным. В
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
рассмотренном |
примере, на |
основании |
|
|
данных |
|
таблицы 2.4. |
мы имеем |
|||||
|
|
= 9,93646 мВ, |
sX = 0,0055 мВ. |
Выражение |
|
для |
кривой плотности |
вероятности |
|||||
X |
|||||||||||||
распределения, согласующееся с экспериментальными данными примет вид |
|
||||||||||||
|
|
|
|
|
|
|
− |
1 |
x−9,93646 2 |
|
|||
|
|
|
p(x)= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
e |
|
2 0,0055 |
|
. |
|
||||
|
|
|
0,0055 2π |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Далее возникает вопрос, чем объясняется расхождение между гистограммой, полученной при обработке опытных данных и подобранным теоретическим распределением: только случайными обстоятельствами, связанными с малым числом наблюдений или в том, что результаты наблюдений имеют иное распределение.
Ответ на данный вопрос могут дать методы проверки статистических гипотез. Идея применения заключается в том, что на основании гистограммы строится гипотеза, что результаты наблюдений подчиняются распределению с плотностью pX (x).
Для проверки гипотезы выбирается мера расхождения теоретического и экспериментального распределения- U. В качестве меры расхождения можно принять сумму квадратов разностей относительных частот попадания в каждый интервал результатов наблюдений и теоретических вероятностей, взятых с некоторыми коэффициентами:
U = ∑r ci (Pi − Pi )2 ,
i =1
где сi -коэффициенты, называемые весами разрядов; Pi -теоретические вероятности,
определяемые как:
X i+1
Pi = ∫ px (X )dx ,
X i
где pX (x)-предполагаемая плотность распределения.
Мера расхождения U является случайной величиной и имеет так называемое χ2 (хи-
квадрат) распределение Пирсона. Примечательно, что мера U подчиняется распределению
χ2 независимо от исходного распределения. Таким образом, данный подход к оценке расхождения теоретических и экспериментальных данных является универсальным.
Дифференциальная функция распределения Пирсона имеет вид:
72
pχ 2 |
(ξ )= |
|
|
1 |
|
|
|
k |
−1 |
е |
− |
1 |
ξ |
|
|
|
|
ξ 2 |
|
2 |
, |
||||||
k |
|
1 |
|
|
|||||||||
k |
|
|
k |
|
|
|
|
|
|||||
|
|
|
|
− 1 ! 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
где k- число степеней свободы распределения, равное k= n-1, т.е. на единицу меньшее числа измерений.
Значения функции справедливы если частоты mi ≥ 5 , число измерений стремится к бесконечности, а веса сi выбираются равными n/Pi. Если при построении гистограммы окажется, что для каких либо интервалов mi < 5 , то соседние интервалы объединяются, то под числом степеней свободы понимается k = r − s , где r -число разрядов (столбиков)
гистограммы, а s - число независимых связей, наложенных на относительные частоты Рi . В
рассматриваемом случае первая связь заключается в том, что число результатов, попавших в последний интервал нельзя считать независимой величиной, поскольку оно равно разности между n и числом попаданий в остальные m −1 интервалы. Другие две связи обусловлены числом параметров закона распределения, необходимых для совмещения с гистограммой. В данном случае определялись значения среднего арифметического и оценка дисперсии и приравнивались к математическому ожиданию и дисперсии предполагаемого нормального
распределения. Поэтому в рассматриваемом |
случае |
s = 3, |
а |
число степеней свободы |
||||||||||||
k = m −3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мера расхождения по К.Пирсону, обозначается через χk2 . Её можно записать в виде: |
||||||||||||||||
|
χk2 = ∑r |
n |
|
(Pi − Pi )2 |
= ∑r |
(mi − nPi )2 |
. |
|||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
i =1 |
Pi |
|
|
i =1 |
nPi |
|
|
||||
Чем меньше сумма, тем меньше оснований сомневаться |
в правильности выбора |
|||||||||||||||
закона распределения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По данным таблицы 2.5 можно для доверительной вероятности α =1− q определить |
||||||||||||||||
|
χ2 |
|
|
; |
χ2 |
|
|
|
|
значений |
χ2 , |
в который мера расхождения |
||||
тот доверительный интервал |
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
k |
|
|
|
|||
|
k; |
|
q |
|
k ;1− |
|
q |
|
|
|
|
|
|
|
||
2 |
|
2 |
|
|
|
|
|
|
|
|||||||
может попасть по чисто случайным причинам. Здесь величина q – вероятность того, что дисперсия не выйдет за границы доверительного интервала. Значения α обычно выбирают в пределах 0,01…0,1.
Если вычисленная по опытным данным мера расхождения χk2 окажется в указанном интервале, то гипотеза принимается. Если χk2 выходит за пределы доверительного интервала, то гипотеза отвергается как противоречащая экспериментальным данным.

|
|
73 |
Описанная методика проверки гипотезы |
о том, что |
данное статистическое |
распределение является распределением с плотностью pX (x), |
называется критерием |
|
согласия χ2 .
Таблица 2.5.
Значения интегральной функции распределения Пирсона χk2 ; P для различныхk и P
k |
|
|
|
P |
|
|
|
0,01 |
0,02 |
0,05 |
0,10 |
0,20 |
0,30 |
1 |
0,000157 |
0,000628 |
0,00393 |
0,0158 |
0,0642 |
0,148 |
2 |
0,0201 |
0,0404 |
0,103 |
0,211 |
0,446 |
0,713 |
3 |
0,115 |
0,185 |
0,352 |
0,584 |
1,005 |
1,424 |
4 |
0,297 |
0,429 |
0,711 |
1,064 |
1,649 |
2,195 |
5 |
0,554 |
0,752 |
1,145 |
1,610 |
2,343 |
3,000 |
6 |
0,872 |
1,134 |
1,635 |
2,204 |
3,070 |
3,828 |
7 |
1,239 |
1,564 |
2,167 |
2,883 |
3,822 |
4,671 |
8 |
1,646 |
2,032 |
2,733 |
3,490 |
4,594 |
5,527 |
9 |
2,088 |
2,532 |
3,325 |
4,168 |
5,380 |
6,393 |
10 |
2,558 |
3,059 |
3,940 |
4,865 |
6,179 |
7,267 |
Приведенные в таблице данные данные охватывают наиболее распространенный диапазон изменения величин k и P . При необходимости можно воспользоваться более полными таблицами распределения Пирсона, приведенными в математических справочниках.
Приведем последовательность вычислений при проверке нормальности распределения согласно критериюχ2 .
1. Данные наблюдений группируют по интервалам и подсчитывают частоты mi , с
которыми результаты наблюдений попадают в i − ый интервал. Те интервалы, которые содержат менее пяти наблюдений, объединяют с соседними интервалами. При этом число степеней свободы k соответственно уменьшается.
2.Вычисляют среднее арифметическое Х и точечную оценку среднего квадратического
отклонения результата наблюдений sX , которые принимают в качестве параметров теоретического нормального распределения с плотностью pX (x).
74
3.Для каждого интервала находят вероятности попадания в них результатов наблюдений приближенно как произведение плотности теоретического распределения в середине интервала на его длину:
P |
≈ p |
X |
i |
+ |
X |
i+1 |
|
X |
|
. |
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
||||||
i |
|
x |
|
|
|
|
|
i |
|
||
4. |
Для каждого интервала вычисляют величины |
χi2 (i = 1,2,3....r ) и суммируют их по |
|||||||||||||||
|
всем i, в результате чего получают меру расхождения χk2 . |
|
|
|
|||||||||||||
5. |
Определяют число степеней свободы k = r −3 |
и , задаваясь уровнем значимости |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q = 1 −α , находят по таблице 3 значения |
|
χ |
2 |
1 |
|
и χ |
2 |
|
|
. Если |
||||||
|
|
|
|
|
1 |
||||||||||||
|
|
|
|
|
|
|
|
k ; |
|
q |
|
k ;1− |
|
q |
|
||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||
|
χ2 |
< χ2 |
≤ χ2 |
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
k ; |
|
q |
|
k ; 1− |
|
q , |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
то распределение результатов наблюдений считают нормальным.
2.3. Погрешности косвенных измерений.
При косвенных измерениях вместо интересующей нас величины измеряются другие величины, связанные с искомой величиной некоторой функцией. Например, вместо
интересующей нас |
величины Y измеряются |
величины |
X 1 ; X 2 |
;...... |
X n , |
связанные с Y |
||
зависимостью |
Y = f (X1; X2 ; ...... |
X n ). |
В |
ходе |
экспериментов |
в результате |
||
измерения X1 ; X 2 ; |
......X n получают |
значения |
x1 ; x2 ; |
.....xn , |
которые |
отличаются от |
||
истинного значения на величину |
погрешности. Таким образом для i −го аргумента имеем |
|
X i = xi − i , где |
i - погрешность измерения Xi . |
|
Таким образом результат измерения величины Y может быть записан |
||
y − |
= f (x1 − |
1; ; x2 − 2 ;.......; xn − n ).. |
Здесь y-результат косвенных измерений, - погрешность.
Если погрешности малы по сравнению с измеряемыми величинами, т.е i / xi <<1,
то можно воспользоваться разложением в степенной ряд, ограничившись членами со второй степенью

75
|
= f (x1; x2......xn ) |
|
n |
|
∂f |
|
|
1 |
n |
|
∂2 f |
2 |
||||||||||
y− |
−∑ |
|
|
i − |
|
|
∑ |
|
|
|
i |
|||||||||||
∂x |
|
|
∂x |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
2 i=1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
Отсюда следует, что результат измерений |
|
|
|
|
|
|
|
|
|
2.17. |
||||||||||||
y = f (x1 ; |
x2 ;.......xn ), |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
а погрешность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
∂f |
|
|
1 |
n |
∂2 f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
=∑ |
|
|
i − |
|
|
∑ |
|
|
|
|
i . |
|
|
|
|
|
|
|
|
(2.18). |
||
∂x |
|
|
∂x |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
i=1 |
|
|
|
2 i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||
В большинстве случаев в виду небольших величин погрешностей и отсутствии резких изменений функции (2.17.) можно пренебречь величинами погрешностей, входящих в выражение 2.18. во второй степени. В этом случае имеем:
n |
|
∂f |
|
|
|
∂f |
|
∂f |
|
|
∂f |
|
|
|
=∑ |
|
xi |
= |
x1 + |
x2 |
+ + |
xn |
(2.19). |
||||||
|
∂x1 |
∂x2 |
∂xn |
|||||||||||
i=1 |
|
∂xi |
|
|
|
|
|
|
|
|||||
Формула 2.19 часто используется для расчета систематической погрешности косвенных измерений, когда известны систематические погрешности измерений аргументов, входящих в 2.17. На практике систематическую погрешность измерений часто принимают равной предельному значению погрешностей средств измерений, используемых в косвенных измерениях величин х1, х2, …xn. В этом случае результирующая абсолютная погрешность получается сложением абсолютных погрешностей как случайных величин, т.е.
|
|
∂f |
2 |
|
2 |
|
|
∂f |
2 |
|
2 |
|
∂f |
2 |
|
2 |
|
|
Y = |
|
|
X |
+ |
|
|
X |
|
|
X |
(2.20) |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
∂x1 |
|
|
1 |
|
|
∂x2 |
|
|
2 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xn |
|
|
|
||||
Относительная погрешность определяется по формуле:
|
Y |
|
|
∂(ln f ) |
2 |
|
2 |
|
|
∂ (ln f ) |
2 |
|
2 |
|
∂ (ln f ) |
2 |
|
2 |
|
|
|
|
|
X |
|
|
|
X |
|
|
X |
|
|||||||
δ = |
|
= |
|
|
|
1 |
+ |
|
|
|
2 |
+.... |
|
|
n |
(2.21) |
|||
|
|
|
|
||||||||||||||||
|
Y |
|
∂x1 |
|
|
∂x2 |
|
|
∂xn |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

76
В том случае, если необходимо оценить случайную погрешность косвенных измерений, то расчет осуществляется с помощью следующей формулы
(2.22).
|
|
|
|
∂f |
2 |
|
|
|
|
∂f |
|
2 |
|
|
∂f |
|
2 |
|
σ |
|
= |
|
|
σ |
2 |
+ |
|
|
σ |
2 |
|
|
σ |
2 |
|||
|
|
|
|
|
|
|
||||||||||||
|
Y |
|
|
∂x1 |
|
|
x1 |
|
|
∂x2 |
|
|
x2 |
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xn |
|
|
|||
Ввыражении (2.22). σx1 , σx2 , σxn - средние квадратические погрешности
измерения величин X1 , X 2 X n . Данное выражение можно использовать для оценки случайных погрешностей если эти погрешности некоррелированные. В противном случае необходимо учитывать коэффициент корреляции. Если определяется суммарная случайная погрешность косвенных измерений при двух аргументах, следует пользоваться формулой:
2 |
2 |
2 |
|
|
σY |
=σx1 |
+ 2ρσx1σx2 +σx2 |
, |
(2.23). |
где ρ - коэффициент корреляции.
При обработки небольшого количества наблюдений, когда расчет осуществляется в соответствии с формулой 2.12 средние квадратические погрешности заменяются их оценками и обозначаются буквой s.
Примеры
В качестве примеров рассмотрим несколько частных случаев. |
|
а) Функция Y = f (X1; X2 ; ......X n ) представляет собой |
сумму |
величин X1 , X 2 X n , взятых с весовыми коэффициентами а1 , а2 ....аn : |
|
n |
|
Y = ∑аi Xi = а1 X1 + а2 X 2 +.....аn X n . |
|
i =1 |
|
Погрешность, с которой произведено измерение величины |
X1 → X1 |
X 2 → X 2 , и ….. X n → X n . |
|
измеренных
,величины
Частные производные |
∂f |
; |
∂f |
|
..... и |
∂f |
равны соответственно: |
а |
, а |
2 |
......а |
n |
. |
|
∂X 1 |
∂X |
|
∂X n |
1 |
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
||||
В соответствии с (2.13) имеем:

77
= а1 X1 + а2 X 2 +....... + аn X n .
Для некоррелированных случайных погрешностей со средними квадратическими отклонениями погрешностей σX1 , σX 2 .......σX n , имеем:
σ 2 |
= а2 |
σ 2 |
+ а2 |
σ 2 |
+...... + а2 |
σ 2 |
. |
Y |
1 |
X1 |
2 |
X 2 |
n |
X n |
|
б) По результатам измерения напряжения U и сопротивления R косвенным образом измерена мощность:
P = U 2 .
R
Систематическая |
погрешность |
измерения напряжения |
U , систематическая |
|
погрешность измерения |
тока |
I . |
Среднее квадратическое |
отклонение результата |
измерения напряжения σU , среднее квадратическое отклонение результата измерения сопротивления σR .
Производная |
∂P |
= |
2 U |
, а |
∂P |
= − |
U 2 |
. |
|
|
|||
∂U |
R |
∂R |
R2 |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||
На основании (2.19) имеем: |
P = |
2U |
|
U − |
U 2 |
R . |
|||||||
R |
R2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
Соответственно для среднего квадратического отклонения результата измерения мощности на основании (2.22) имеем:
2 |
|
4U 2 |
2 |
|
U 4 |
2 |
|
σP |
= |
|
σU |
− |
|
σR . |
|
R2 |
R4 |
||||||
|
|
|
|
|
78
Глава 3. Нормирование погрешностей средств измерений
При поверке средств измерений (СИ) определяют, не выходят ли их погрешности (а так же некоторые другие показатели) за установленные пределы, не превышают ли они допускаемые значения. Возникает вопрос: “ А как устанавливаются эти значения?”.
Имеется два принципиально разных подхода к решению этой задачи. Первый подход заключается в установлении для конкретного средства измерений класса точности. Единые правила установления пределов допускаемых погрешностей показаний по классам точности регламентирует ГОСТ 8.401-80. Под классом точности СИ понимают их обобщенные характеристики, определяемые пределами допускаемой основной и дополнительной погрешности. Класс точности не определяет однозначно точность измерений. Фактически класс точности определяет предельное, гарантированное значение погрешности для данного типа средств измерений. При этом нет деления на погрешность систематическую и случайную. Оба вида погрешностей нормируются в виде предела основной и дополнительной погрешности. ГОСТ 8.401-80 не устанавливает классы точности СИ, для которых предусмотрены нормы отдельно для систематической и случайной составляющих погрешностей, а так же если необходимо учитывать их динамические характеристики. Классы точности устанавливаются в тех случаях, когда погрешности СИ могут быть выражены числом или сравнительно простой формулой.
Нормирование погрешностей СИ с помощью класса точности имеет существенные недостатки, сводящиеся к тому, что погрешности СИ имеющие разное происхождение оцениваются суммарно в виде одного числа. При этом невозможно определить, какова величина систематической составляющей погрешности СИ, и какова, величина случайной составляющей погрешности. Если СИ используется совместно с другими СИ, например в составе измерительного комплекса, затрудняется определение общей погрешности. Другим недостатком является то, что погрешность в большинстве случаев оказывается завышенной. Не случайно говорится не о допускаемой погрешности СИ, а о «пределе» допускаемой погрешности. Если выпущена партия СИ, то далеко не все из них будут иметь предельное значение погрешности, установленное классом точности, однако при расчетах придется пользоваться предельным значением погрешности, соответствующим его классу точности. Наконец, следует отметить еще один недостаток нормирования погрешности СИ с помощью класса точности. В настоящее время требования к допустимым отклонениям характеристик
79
каналов связи является настолько высокими, что рабочие СИ (особенно ранних выпусков, но находящиеся на эксплуатации) не удовлетворяют потребностей практики. В этом случае приходится прибегать к специальным мерам, позволяющим уменьшать величины отдельных составляющих погрешности. Однако при использовании классов точности величины отдельных составляющих не известны и эффект, получаемый в этом случае, не может быть оценен.
Новый подход к определению погрешностей СИ нашел свое отражение в ГОСТ 8.009-84 “ Нормирование и использование метрологических характеристик средств измерений”. Данный стандарт устанавливает комплекс метрологических характеристик, которые должны быть известны при выпуске СИ. Комплекс нормируемых характеристик должен быть полным и позволять производить расчет погрешностей СИ не только в нормальных условиях, но и в реальных условиях эксплуатации. Несмотря на преимущества этого способа, оценка погрешностей СИ на основе класса точности, является достаточно распространенной применительно к электроизмерительным СИ и ее целесообразно рассмотреть подробно.
3. 1.Классы точности средств измерений.
Классы точности устанавливаются стандартом исходя из величин абсолютной или относительной погрешности. Предел допускаемой основной абсолютной погрешности может быть представлен одним из трех способов: постоянным для любых значений измеряемой величины “x” числом, характеризующим аддитивную погрешность
П = ±а; |
(3 .1) |
В виде двухчленной формулы, учитывающей как аддитивную, так и мультипликативную погрешности
П =± (а + вх); |
(3. 2) |
в виде уравнения
П = f (x) |
(3.3) |
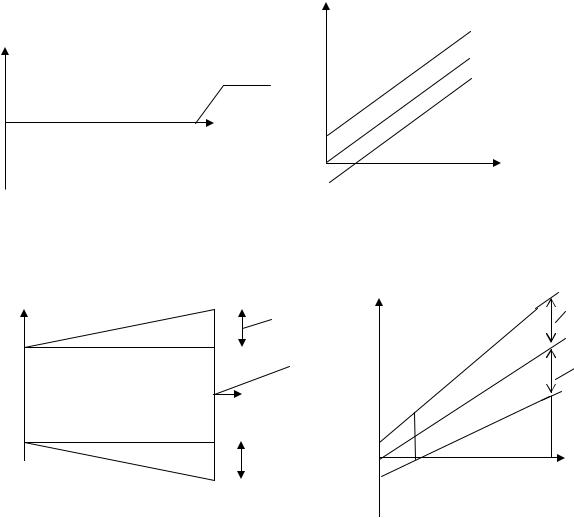
80
При сложной зависимости (3.3) допускается представлять погрешность в виде графика или таблицы.
При применении формул (3.1) предполагается, что границы абсолютных погрешностей неизменны. Графически это показано на рис. 3.1а. Такой вид погрешности носит название аддитивной. Он имеет место в стрелочном приборе в том случае, когда перед началом измерений не был установлен ноль показаний. На рис. 3.1. показана характеристика преобразования средства измерений у = φ(х), представляющая собой зависимость
у
|
|
|
|
П = ±а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
+а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-а |
|
|
|
|
|
|
-а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
а) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|||||||||
П = ±(а + вх) |
|
|
вх |
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(а+вх) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+а |
|
|
|
|
|
|
Х к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-(а+вх) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
+а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
- вх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ХК |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в)
г)
Рис.3.1
81
показания средства измерения от входного сигнала. Область возможных отклонений характеристики преобразования в этом случае на рис. 3.1б заштрихована. Границы этой области параллельны идеальной характеристике преобразования обозначенной на рис.3.1б пунктирной линией.
На рис. 3.1в представлен вид поля допуска для случая, когда нормируется погрешность прибора согласно формуле П =± (а + вх). Соответствующая функция преобразования средства измерения и поле допуска представлены на рис. 3.1г.
Как видно из рис 3.1в и г поле допуска расширяется по мере увеличения показания СИ. При нормировании погрешности в соответствии с формулой учитывается, что СИ имеет не только аддитивную погрешность. Вторая составляющая погрешности, зависящая от измеряемой величины носит название мультипликативной. В формуле (3.2) коэффициент “а” отражает аддитивную составляющую погрешности, а “в”- мультипликативную. Если коэффициент “в”, отражающий мультипликативную составляющую равен нулю, то формула (3.2) превращается в формулу (3.1). Возможен случай, когда присутствует только мультипликативная составляющая, т.е. когда а = 0 и П = вх. В этом случае поле допуска принимает вид, показанный на рис. 3.2а. Соответствующее поле допуска относительно функции преобразования показано на рис. 3.2б.
П =±вх |
|
у |
|
|
|
|
|
|
|
+вх |
||||||
|
|
|
|
|
|
|
|
|||||||||
ХК |
|
|
|
|
|
|
-вх |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
х |
|
|
|
|
|
|
|
|
|
|
|
ХК |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
б) |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
Рис.3.2. |
|
|
|
|
|
|
|
||||||||
82
При установлении класса точности пользуются и пределами допускаемых относительных погрешностей. Пределы допускаемой относительной погрешности для случая (3.2) выражаются формулой:
δП = ± |
П |
= ±q, |
(3.4 ) |
|
x |
||||
|
|
|
В случае когда абсолютная погрешность монотонно увеличивается от начала к концу диапазона (рис. 3.1б и формула 3.2), предел допускаемой относительной погрешности определяется формулой.
|
|
|
|
|
Хк |
|
|
|
(3.5) |
|
|
|
|||||||
δП |
= ± c + d |
|
|
|
|
|
−1 |
|
|
х |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Где “c” и “d” –постоянные числа, Хк - предел измерения, х – измеряемая величина.
Поля допусков для формул (3.4) и ( 3.5 ) представлены на рис.3.2 а и б соответственно.
δП |
δ П |
с
x |
х |
|
Хк |
||
ХК |
||
|
||
а) |
|
б)
Рис. 3.3.
Как видно из графиков рис. 3.1 - 3.3 за исключением графиков на рис. 3.1а,б величины абсолютных и относительных погрешностей зависят от измеряемой величины. Иными словами погрешности средств измерений различны в различных точках шкалы. Это обстоятельство учитывается при нормировании погрешностей средств измерений по классу
83
точности. Правила нормирования устанавливают таким образом, что бы по классу точности можно было бы, во-первых, сравнивать средства измерений друг с другом, во-вторых, при необходимости можно было бы рассчитать погрешность при измерении конкретной величины.
Сравнение средств измерений на основании класса точности можно осуществить при условии, если нормирование будет осуществлено на основе относительной погрешности. Действительно, при сравнении по абсолютной погрешности двух частотомеров, погрешность в 1 МГц будет недопустимо большой для частотомера с диапазоном измерений в 10 МГц, и весьма малой для частотомера с диапазоном в 10 ГГц. На самом деле, оценка по относительной погрешности покажет в первом случае погрешность в 10%, а во втором 0,01%. Ясно, что второй частотомер более точен.
Для уяснения смысла коэффициента “c” представим, что прибор, предел допускаемой погрешности которого нормирован формулой 3.5, показал значение, равное верхнему значению предела диапазона измерения; х = Хк. В этом случае выражение в круглых скобках обращается в нуль и мы получаем, что предел допускаемой относительной погрешности δП = с. Таким образом, с - предел допускаемой относительной погрешности при максимальном показании прибора. Для уяснения смысла коэффициента d преобразуем формулу 3.5
|
= |
1 |
[d X К + (с − d )x ] |
(3.6) |
||||
П |
100 |
|||||||
|
|
|
|
|
|
|||
Если показание прибора равно нулю (т.е. х=0), то |
|
= |
1 |
d X К . Отсюда видно, что d- |
||||
П |
100 |
|||||||
|
|
|
|
|
|
|||
предел допускаемой погрешности при нулевом показании прибора, выраженный в процентах от верхнего предела измерений. Разность коэффициентов с и d характеризует возрастание относительной погрешности при уменьшении показания прибора, так же как выражение в формуле 3.5 характеризует возрастание относительной погрешности при уменьшении показаний прибора. Формулу 3.5 широко применяют при нормировании погрешности средств измерений сравнительно высокой точности, например цифровых приборов, многозначных мер сопротивления. Для удобства сравнения средств измерений по точности введено понятие приведенной погрешности. Приведенная погрешность может быть определена на основе следующей формулы:
|
|
|
84 |
γ = |
П |
100 . |
( 3.7) |
|
|||
|
ХК |
|
|
В этой формуле Х К – нормирующая величина, |
равная конечному значению шкалы |
||
прибора. Таким образом, независимо от диапазона измерений при нормировании погрешности, она «приводится» к конечному значению шкалы конкретного прибора. По этой причине погрешность называется приведенной. Так же как и при нормировании по абсолютной погрешности, так и по относительной указывается то предельное значение погрешности, которое допускается для конкретного типа прибора.
Вернемся к формулам (3.1) – (3.3). Здесь П - пределы допускаемой абсолютной основной погрешности, выраженные в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы, х –значение измеряемой величины на входе (выходе) средства измерений или число делений, отсчитываемых по шкале; “а” и “в” положительные числа, не зависящие от показаний прибора.
В формулах (3.4) и (3.5) δП - пределы допускаемой относительной основной погрешности. Обычно относительная погрешность выражается в процентах. В формуле (3.4) q – отвлеченное число. В формуле (3.5) “с и “d” – положительные числа, не зависящие от показаний прибора, а Хк – больший по модулю пределов измерений (конечное значение шкалы). Конкретные значения величин “q”, “с” и “d” выбираются из
ряда 1 10n ; 1,5 10n ; ( 1,6 10n ); 2 10n ; |
2,5 10n ; ( 3 |
10n ); 4 10n ; 5 10n ; 6 10n ( n =1;0 ;-1; |
||||||||
-2 и т.д.). |
|
|
|
|
|
|
|
|
|
|
Величины “c” и |
”d” могут быть определены через коэффициенты “а” и “в” по |
|||||||||
следующим формулам. |
|
|
|
|
|
|
|
|
|
|
|
С= в+d |
|
|
|
|
|
(3.8) |
|||
|
a = d |
|
X K |
|
= ±а или |
|
|
|
(3.9) |
|
|
|
|
|
|
|
|||||
При применении |
формул |
П |
δ |
П |
= |
П |
= ±q для нормирования |
|||
|
||||||||||
|
|
|
|
|
|
|
ХП |
|||
погрешностей средств измерений, следует учитывать, что погрешность каждого отдельного
85
средства измерений не должна превышать указанной нормы, оставаясь только положительной или только отрицательной.
Способ выражения погрешностей для конкретного средства измерений выбирают в зависимости от характера изменения погрешности по диапазону измерения. В случае, когда средство измерений имеет только аддитивную погрешность или аддитивная погрешность настолько велика, что мультипликативной погрешностью можно
пренебречь, предел допускаемой абсолютной погрешности П будет постоянным по диапазону, в то время как предел допускаемой относительной погрешности будет изменяться по гиперболе (рис.3.3 а). В этом случае удобнее нормировать абсолютную погрешность по указанной формуле П = ±а.
В средствах измерений, с преобладающей мультипликативной погрешностью, наоборот удобнее нормировать предел допускаемой относительной погрешности.
Действительно, положим в (3.2) коэффициент “ а” равным нулю. Тогда П = ±вх и,
следовательно, предел абсолютной погрешности изменяется по линейному закону, как это
показано на рис.3.4а. Предел допускаемой относительной погрешности δП = ± |
П |
= ±в не |
|
х |
|||
|
|
зависит от измеряемой величины (рис.3.4 б) и, следовательно, характеристика средства измерения может быть выражена одним числом. Так, например, нормируют погрешность мостов постоянного и переменного тока.
П |
δП |
|
|
х |
|
|
|
х |
0 |
0 |
|
|||
|
|
|
|||
|
хК |
|
хК |
||
|
|
|
|
|
|
а) |
б) |
|
|
|
Рис.3.4 |
Для нормирования погрешностей средств измерений с аддитивной и мультипликативной погрешностями применяют формулы (3.2) или (3.5), причем
86
достаточно задать величины коэффициентов "а" и "в" или "c" и "d". Эта формула широко применяется для нормирования погрешностей средств измерений высокой точности, таких как цифровые приборы, многозначные меры и т.п.
Например, основная погрешность потенциометра Р307 устанавливается формулой:
= ±(0,5 + 150U )10−6 В , в которой а = 0,5· 10-6, а в = 150· 10-6.
Аналогично погрешность установки частоты генератора Г3-113 задана формулой:
= ±(0,5 +0,005f) Гц, в которой а = 0,5, а в = 0,005.
Знание только абсолютной погрешности не позволяет сравнивать между собой приборы с разными диапазонами измерений. Оценка же погрешностей с помощью формулы 3.4. позволяет это сделать.
Кроме вышеперечисленных способов нормирования погрешностей ГОСТ 22261-82 устанавливает следующий способ выражения пределов допускаемой относительной погрешности:
|
|
|
|
|
|
|
|
|
= Аlg |
|
1 |
+ |
П |
(3.10) |
|
П |
|
|
, |
||||
|
|||||||
|
|
|
|
|
X Д |
|
|
Где П − абсолютная погрешность; ХД - действительное значение измеряемой величины;
А=10 - при измерении мощности, энергии, плотности энергии и других энергетических величин; А=20 – при измерении напряжения, силы тока, напряженности поля и других силовых величин.
Пределы допускаемых погрешностей в форме абсолютных и относительных погрешностей устанавливают также в виде:
-линейной функции от значения измеряемой величины или влияющих величин
П;δ П = а0 + а1 хП |
(3.11) |
- полиномом
n
П;δП = ∑аi хimi. (3.12)
i=0

87
Допускается также выражать П и δП в виде таблицы или графика. Обозначения классов точности различных средств измерений и формулы для расчета погрешностей приведены в таблице 3.1.
Таблица 3.1
Обозначение класса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пределы допускаемой основной |
|||||||||||||||
точности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
погрешности. |
|
|
|
|||||||
В |
На средстве |
Формула выражения |
Абсолют- |
Относитель- |
|
Приведен- |
||||||||||||||||||||||||||
документа- |
измерений |
|
|
|
ная |
|
|
|
ная |
|
|
|
ная |
|||||||||||||||||||
ции |
|
|
погрешности |
погреш- |
погрешность- |
погреш- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность- |
|
П |
|
δ П , % |
|
|
ность |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ ,% |
|
1.Класс |
Р –если ХN |
Приведенная: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
точности |
выражена в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p (например |
единицах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X N |
|
|
|
± p |
X N |
|
|
|
|
± p |
|
|
||
0,5) |
измеряемой |
|
|
|
|
|
|
|
|
|
|
|
|
|
± p |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||
|
величины, р- |
γ = |
|
|
|
100 = ±p |
100 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Если ХN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
X N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
определяется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
X N -нормирующая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
длиной шкалы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.Класс |
|
Относительная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
точности q |
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
± q |
|
x |
|
|
|
± q |
|
|
|
|
± q |
x |
|
||||
(Например |
|
δ = |
|
|
100 = ±q |
|
100 |
|
|
|
|
|
|
|
|
X N |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0,1) |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Относительная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
δ = |
|
|
= |
|
|
a + bx |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
± |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
X K |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3.Класс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X K |
|
|
где |
|
|
|
|
|
|
± c + d |
x |
−1 |
|
|
|
|||||||||||
точности c/d |
с/d |
= ± c + d |
|
|
|
− |
1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a = d X K , |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b=c-d |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.Класс |
M |
|
|
|
|
П = ±a |
|
|
|
|
|
|
|
Указывается в стандартах |
|
|
||||||||||||||||
точности М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Класс |
|
|
П = ±(а+ вХП ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
точности С |
С |
|
|
|
|
|
|
|
Указывается в стандартах |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2.Примеры расчетов погрешностей.
1.Класс точности вольтметра 1,5. Верхний предел измерений X K = 100В. Показание прибора Х=50 В. Шкала прибора и положение стрелки показаны на рисунке.
88
50 В
0 |
|
100 В |
|
Определить абсолютную, относительную и приведенные погрешности.
Решение. Согласно таблице, обозначение класса точности 1,5 означает, что у вольтметра нормирована приведенная погрешность, т.е γ=1,5% причем нормирующая величина X N
выражена в вольтах, т.е. X N = X K = 100В. Согласно приведенным в строке 1 формулам,
имеем:
= ±p 100X N = ±1,5 100100 = ±1,5В ; δ = ±p XxN = ±1,5 10050 = ±3%.
2.Класс точности вольтметра 1,5. Верхний предел измерений +100 В, нижний -100 В. Показание прибора X=50 В. Шкала и положение стрелки показаны на рисунке.
0
+50 В
-100 В |
+100 В |
|
Определить абсолютную, относительную и приведенные погрешности.
Решение.
Поскольку шкала прибора имеет нуль посредине, величина X N определяется как сумма модулей пределов измерений, т.е. X N = 100 +100 = 200В . Поскольку цифра, означающая класс точности, указана в задании без кружочка, нормирована приведенная погрешность,
т.е.γ = 1,5%. Абсолютная погрешность = ±γ X N = 1,5 200 = ±3,0В. Относительная погрешность определится как абсолютная погрешность, отнесенная к показанию прибора, т.е. к 50 В:
δ= ± 100 = ± 3,0 100 = ±6%.
x50

89
3. Класс точности прибора 1,5. Верхний предел измерений +100 В, нижний предел + 25 В. Показание прибора 50 В. Определить абсолютную, относительную и приведенную погрешности.
50 В
25 В |
+100 В |
|
Решение.
Поскольку класс точности указан в виде цифры без кружочка, у данного прибора
нормирована приведенная погрешность γ=р=1,5, причем |
|
X N |
равняется большему из |
||||
пределов измерений, т.е. 100 В. Приведенная погрешность γ |
равная классу точности, т.е. |
||||||
1,5%. Предел допускаемой абсолютной погрешности |
|
= ±γ X N = ±1,5 100 = ±1,5В. |
|||||
Предел допускаемой относительной погрешности для точки |
шкалы, |
соответствующей |
|||||
|
|
|
|
1,5 |
100 = ±3%. |
||
показанию прибора 50 В, определится из формулы: δ = ± |
|
100 = ± |
|
||||
xп |
50 |
||||||
4.Класс точности 1,0 . На средстве измерений класс точности обозначен |
1,0 |
||||||
Длина шкалы прибора X N =10 см, показание прибора X=5 см, что соответствует 100 Ом.
Внешний вид шкалы прибора показан на рисунке. Определить абсолютную и относительную погрешности.
|
100 Ом |
∞ |
0 |
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как |
предел |
допускаемой погрешности указан в виде числа изображенного над |
|||||||||||||
галочкой, |
нормирована приведенная погрешность, т.е. γ = |
|
100 = ±1,0. Относительная |
||||||||||||
X N |
|||||||||||||||
погрешность δ = ± |
|
|
= ±p |
X N |
= |
1,0 |
10 |
= 2,0 %. Абсолютная погрешность определится как |
|||||||
x |
|
5 |
|||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|||||
= ±δ |
x |
|
= ±2,0 |
100 |
= ±2 |
Ом. |
В |
числителе величина x |
соответствует показанию |
||||||
100 |
100 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
прибора, т.е. 100 Ом.

90
5. Класс точности прибора 0,2 /0,1. Показание прибора х=33,3 В, конечное значение шкалы
X K = 99,9. Определить абсолютную и относительную погрешности.
Решение.
Способ нормирования погрешности, а также конечное значение шкалы 99,9В
свидетельствует, что прибор является цифровым и для решения задачи можно воспользоваться формулами, имеющимися в строке 3 таблицы. В соответствии с таблицей
с= 0,2%, а d= 0,1%.
Относительная погрешность
|
|
|
|
X |
K |
|
|
|
|
|
|
|
99,9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
δ = ± |
|
c + d |
|
|
|
−1 |
= ± |
0,2 |
+0,1 |
|
|
|
|
|
−1 |
= ±0,4%. |
|
|
|
|
|||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
33,3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||||
Для определения абсолютной погрешности вычислим предварительно
коэффициенты: a = dX K = 0,1 99,9 = 9,99. , в |
= с- |
d = 0,2 – 0,1=0,1. Следовательно, |
|||||
абсолютная |
погрешность |
в соответствии |
со |
строкой 3 таблицы составит: |
|||
= |
a + bx |
= |
9,99 +0,1 33,3 |
= 0,13В . |
|
|
|
|
100 |
|
|
|
|||
100 |
|
|
|
|
|
||
6. Класс точности прибора 1,5. На приборе класс точности обозначен 1.5
Показание прибора х=50 В. Определить абсолютную и приведенные погрешности
50 В
0 |
|
100 В |
|
Решение.
Поскольку класс точности указан цифрой в кружке, у данного прибора нормирована относительная погрешность. Следовательно δ = q = 1,5 . Согласно таблице 3.1 строка 2

91
имеем: абсолютная погрешность = 100δx = 1,510050 = ±0,75 В. Приведенная погрешность
γ = ± X K 100 = ± 0,75100 100 = ±7,5% .
3.3. Особенности нормирования погрешностей средств измерений с неравномерной шкалой.
Некоторые средства измерений изготовляются с неравномерной шкалой. Неравномерная шкала имеет преимущества в тех случаях, когда диапазон измеряемой величины чрезвычайно велик и имеется целесообразность не делить его на поддиапазоны. К таким средствам измерений можно отнести омметры. В некоторых случаях неравномерная шкала необходима для правильного отображения контролируемых процессов, например измерение тока в цепях с временными перегрузками. Например, перегрузочные амперметры имеют растянутую шкалу в начале диапазона измерений и сжатую шкалу в конце. Такие приборы позволяют с удобством контролировать величину тока в стационарном режиме, так как стрелка находится в районе средины шкалы, и не зашкаливают при кратковременных бросках тока, например при пуске мощного электродвигателя.
Нормирование погрешности перегрузочных амперметров.
Напомним, что в обычных амперметрах предел допускаемой погрешности нормируется в виде приведенной погрешности. За нормирующее значение принимают конечное значение шкалы X K и сумму абсолютных значений начала и конца диапазона измерений у приборов, имеющих двухстороннюю шкалу (нулевая отметка в средине
шкалы). Абсолютная погрешность при этом определяется по формуле = γ |
Х к |
. |
|
100 |
|||
П |
|
Диапазон делится на два поддиапазона: диапазон измерений, предназначенный для измерений в нормальном режиме работы, и перегрузочную часть, предназначенную для измерений при кратковременных перегрузках цепи.
Основная погрешность таких амперметров нормируется в пределах основного диапазона измерений - в процентах от его конечного значения, в пределах перегрузочной части шкалы в процентах от разности конечной значений перегрузочной части шкалы и
92
диапазона измерений. Предел допускаемой основной погрешностиγ в пределах диапазона измерений численно равен обозначению класса точности, а в пределах перегрузочной части шкалы выражается формулой
γ = |
p I K |
L |
, |
|
(3.13) |
2 I P |
l |
|
|||
|
|
|
0,4 |
0,6 |
|
|
0,2 |
|
|
0,8 |
IK |
0 |
|
|
|
mA |
10 |
|
|
|
|
Ip 
Рис. 3.5.
где p – числовое обозначение класса точности, L - длина всей шкалы, мм; l- длина перегрузочной части шкалы, мм; I K и I P - конечные значения основного диапазона измерений и перегрузочной части шкалы. На рис.3.5 основной диапазон от 0 до 0,8 мА и от 0,8 мА до 10 мА перегрузочная часть, конечное значение основного диапазона
IK= 0,8, перегрузочного IP=10 мА
Нормирование погрешностей омметров с неравномерной шкалой.
Омметры с неравномерной шкалой имеют шкалы от нуля или некоторой величины до ∞. Допускается два способа нормирования.
Способ 1.
Нормируется погрешность в процентах от показания. В этом случае δ = ± RП 100% и
П = ± 100δR Ом.
Такой способ применен в омметрах М57Д, ТТ-1 , тераометре Е6-13А и др.
Пример.

93
Омметр М57Д. Показание 500 Ом. Относительная погрешность δ = ±10% . Определить абсолютную погрешность.
П = ± 100δR = ± 10100500 = ±50 Ом.
Способ 2.
Нормируется погрешность в процентах от длины всей шкалы. При этом
П |
= ±γ |
|
LР |
|
(3.14) |
|
|
|
100S |
|
|||
|
|
|
|
|||
γ = ± |
П |
S 100 , |
(3.15). |
|||
|
||||||
|
|
LP |
|
|||
где LП длина рабочей части шкалы в мм, S- чувствительность омметра в данной точке шкалы, т.е. длина участка шкалы, приходящаяся на единицу сопротивления вблизи поверяемой отметки, мм/Ом. Длина всей шкалы или рабочей части при отсутствии ее значения в документации измеряется любым способом, но с погрешностью не более 10%. Для определения абсолютной погрешности в конкретной точке щкалы используется следующая формула
П = ±γ LP |
(Rср + R )2 |
, |
(3.16) |
|
100 LRср |
||||
|
где RСР - сопротивление, соответствующее геометрической средине шкалы на данном диапазоне измерений, Ом; R- показание в Ом, LP - длина рабочей части шкалы, L- длина всей шкалы.
Для определения Rcр через средину шкалы проводят линию, пересекающую шкалу в геометрической средине. Сопротивление, отсчитанное в единицах измеряемой величины (Ом, кОм) по шкале омметра на пересечении с проведенной линией и умноженное на множитель соответствующего диапазона измерений (для многодиапазонных приборов),
является исходной величиной для определения Rcр . Если Rcр отсчитать трудно, так как оно находится между отметками шкалы, то к омметру можно подключить магазин сопротивлений и, подобрав величину сопротивления, установить стрелку на геометрическую средину. Отсчет взять с магазина сопротивлений.
94
Нормирование погрешностей измерителей уровня.
Большинство аналоговых вольтметров переменного тока кроме обычной шкалы для измерения напряжения имеют специальную шкалу, предназначенного для измерений относительного уровня напряжения переменного тока в децибелах. Эти приборы находят широкое применение для оценки затухания, ослабления и усиления сигналов в проводной связи и радиотехнике. Шкалы измерительных приборов Ц4313, Ц4354, Ф4318, а также электронные вольтметры В3-36, В3-42, ВК7-9 имеют отметку “ Децибелы”.
Измеритель уровня напряжения представляет собой вольтметр, шкала которого проградуирована в децибелах. По ГОСТу в отрасли ”Cвязь” уровень обозначается буквой L (не следует путать с обозначением индуктивности). При градуировке шкалы пользуются соотношением
L = 20lg |
U |
(3.17.) |
|
|
, |
||
0,775 |
|
||
где L- относительный уровень напряжения, дБ; U- измеряемое напряжение, В; 0,775 – напряжение, относительно которого производится измерение.
Данное выражение является уравнением шкалы измерителя относительного уровня напряжения, имеет логарифмический характер и отличается неравномерностью – в начале она сжата, к концу сильно растянута. За нулевую отметку принимают напряжения 0,775 В , что соответствует мощности 1 В на сопротивлении 600 Ом.т
Существуют два варианта исполнения шкал в децибелах, которые отличаются друг от друга расположением отметки 0 дБ. У одних приборов отметка 0 дБ совпадает с отметкой 0,775 Вт в диапазоне измерений 0-1 В (Ц4315, В3-42), у других- с отметкой 0,775 В в диапазоне 0,3 В (Ц4324, Ц4353).
Так как измеритель уровня - это обычный вольтметр переменного тока, шкала которого проградуирована в децибелах, то пределы допускаемой основной абсолютной погрешности его как вольтметра можно вычислить по формуле
П |
= ±γ |
|
U К |
, |
(3.18.) |
|
100 |
||||||
|
|
|
|
|||
где γ - предел допускаемой основной приведенной погрешности вольтметра, %;
U К - конечное значение диапазона измерений вольтметра, В.

95
Из формулы (3.16), для случая, когда : U=UK ,а L=LK :
LK |
(3.19.). |
UK =0,775 10 20 |
Подставляя (3.19) в (3.18), получаем:
|
=± |
0,775 |
γ |
|
|
LK |
|
(3.20.) |
П |
|
|
10 |
20 |
, |
|||
100 |
|
|||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
где LK - конечное значение диапазона измерений измерителя относительного уровня.
3.4. Нормирование метрологических характеристик средств измерений.
3.4.1.Основные особенности решаемой задачи.
При нормировании погрешностей средств измерений путем установления класса точности, средству измерения приписывается некий предел допускаемой абсолютной или относительной погрешности. Величина этого предела является оценкой погрешности сверху, т.е. для многих образов приборов данного типа она оказывается завышенной. Требования к точности средств измерений применяемых в отрасли “Связь” постоянно возрастает. Необходима более достоверная оценка погрешности средства измерений в конкретных условиях их применения. В ряде случаев приходится определять индивидуальные метрологические характеристики средства измерения и с их помощью рассчитывать реальную погрешность. Важно так же иметь возможность оценить отдельные составляющие погрешности, которые в ряде случаев можно исключать или уменьшить, применяя определенные методы измерений. Все это привело к разработке ГОСТ 8.009-84 “Нормирование и использование метрологических характеристик средств измерений”. Указанный стандарт дополнен весьма обстоятельным методическим материалом по его применению - РД50-453-84. “Нормирование метрологических характеристик средств измерений”. Данный стандарт позволяет произвести расчет погрешностей средства измерений в реальных условиях эксплуатации.
В теории и практике измерений наиболее широко используются показатель точности, базирующиеся на принципах теории вероятностей и математической статистики.
96
Такой подход предполагает, что погрешности средства измерений являются случайными функциями и вызываются совместными действиями детерминированных дестабилизирующих факторов, и, следовательно, погрешность средства измерений при каждой его поверке должна рассматриваться как случайная величина. При определенных условиях (время фиксировано, входная величина постоянна) погрешность в каждой точке шкалы средства измерений будет полностью характеризоваться функцией распределения вероятности погрешности. Однако задавать эту погрешность в каждой точке шкалы невозможно, поэтому выбирают один - два числа и статистически описывают точность средства измерений.
Учитывая это, ГОСТ 8.009-84 вводит статистические методы нормирования метрологических характеристик (МХ) средств измерений.
3.4.2. Общие требования к нормируемым характеристикам средств измерений.
Метрологические характеристики средств измерений - характеристики оказывающие влияние на результаты и погрешности измерений, предназначенные для оценки технического уровня и качества средства измерений, для определения результатов измерений и расчетной оценки характеристик инструментальной составляющей погрешности измерений.
Исходя из того, что оценка погрешности измерений осуществленная расчетным путем, она практически сводится к суммированию ее различных составляющих – основной и дополнительной погрешностей средства измерений; динамической методической погрешности; составляющих, обусловленных конечными входными и выходными импедансами средств измерений, большая часть которых представляют случайные величины или случайные процессы. ГОСТ 8.009-84 устанавливает нормируемые МХ такими, чтобы можно было осуществлять статистическое суммирование составляющих погрешностей измерений, так же составляющих погрешности средств измерений. Кроме того, нормируемые МХ должны:
•давать исчерпывающую характеристику всех метрологических свойств средств измерений;
•отражать определенные физические свойства средства измерений;
97
•служить основой для расчета некоторых производных характеристик, соответствующих различным критериям сравнения средств измерений между собой;
•легко контролироваться.
Статистический подход к нормированию погрешностей средств измерений может первоначально казаться достаточно странным, поскольку средства измерений обладают систематической погрешностью. По определению систематическая погрешность детерминированная величина. Действительно для определенного средства измерений систематическая погрешность является величиной детерминированной. Однако если рассматривать совокупность однотипных средств измерений, систематическая погрешность окажется индивидуальной для каждого средства измерений. Таким образом для типа средств систематическая погрешность проявляется как случайная величина. Поэтому при нормировании МХ средств измерений, следует учитывать возможность метрологических свойств, как типа средств измерений, так и конкретных экземпляров данного типа.
3.4.3. Номенклатура нормируемых метрологических характеристик.
Всвязи с тем, что в данном разделе появляются новые термины в конце каждого раздела будут даваться необходимые пояснения терминов. Пояснения заключены в рамки.
а) Характеристики, предназначенные для определения результатов измерений
(без введения поправки):
Функция преобразования измерительного преобразователя, а так же измерительного прибора с неименованной шкалой или шкалой, градуированной в единицах, отличных от единиц входной величины f(x);
значения однозначной или многозначной меры; цена деления прибора или многозначной меры;
вид выходного кода, число разрядов кода цена единицы наименьшего разряда кода средств измерений, предназначенных для выдачи результата в цифровом коде.

98
Функция преобразования измерительного преобразователязависимость информативного параметра выходного сигнала измерительного преобразователя от информативного параметра его входного сигнала.
Информативный параметр входного сигнала средства измерения - параметр входного сигнала, функционально связанный с измеряемой величиной и используемый для передачи её значения.
Информативный параметр выходного сигнала средства измерения - параметр выходного сигнала, функционально связанный с информативным параметром входного сигнала измерительного преобразователя.
Функция преобразования измерительного прибора - зависимость информативного параметра выходного сигнала измерительного прибора от информативного параметра его входного сигнала.
б) Характеристики погрешности средств измерений:
характеристики систематической составляющей S погрешности средств измерений выбирают из числа следующих.
Значение |
систематической составляющей |
S |
или |
значение |
систематической |
||
составляющей |
S , математическое |
ожидание |
M [ |
S ] |
и среднее |
квадратическое |
|
отклонение σ [ |
S ] систематической составляющей погрешности. |
|
|||||
|
|
|
o |
|
|
|
|
Характеристики случайной составляющей |
погрешности средств измерений: |
||||||
|
|
|
|
|
|
|
o |
среднее квадратическое отклонение σ o |
случайной составляющей погрешности |
||||||
|
|
|
|
|
|
|
|
или нормализованная автокорреляционная функция ro (τ ), или функция спектральной |
|||||||
плотности S o (ω) случайной составляющей погрешности ; |
|
|
|||||
характеристика |
|
|
o |
|
|
|
|
случайной составляющей H погрешности от гистерезиса – вариация Н |
|||||||
выходного сигнала (показания средства измерений).
Характеристики чувствительности средств измерений к влияющим величинам выбирают из числа следующих:
•функции влияния ψ (ξ ),
•изменения ε(ξ) значений метрологических характеристик (МХ), вызванные
изменениями влияющих величинξ в установленных пределах.
Динамические характеристики средств измерений
99
Полные динамические характеристики:
•переходная характеристика h (t);
•импульсная переходная характеристика g(t);
•амплитудно-фазовая характеристика G(jω t);
•амплитудно-частотная характеристика А(ω) для минимально-фазовых средств измерений;
•совокупность амплитудно-частотных и фазо-частотных характеристик;
•передаточная функция G(S).
Частные динамические характеристики аналоговых средств измерений, которые можно рассматривать как линейные.
К частным динамическим характеристикам относят любые функционалы или параметры полных динамических характеристик:
•время реакции tr ;
•коэффициент демпфирования γdem ;
•постоянную времени Т;
значение амплитудночастотной характеристики на резонансной частоте.
•Частные динамические характеристики аналого-цифровых преобразователей (АЦП) и цифровых измерительных приборов (ЦИП), время реакции которых не превышает интервала времени между двумя измерениями, соответствующего максимальной частоте (скорости) измерений:
•время реакции tr ;
•погрешность датирования отсчета td ;
•максимальная частота (скорость измерения) fMAX ;
Частные динамические характеристики ЦАП:
•время реакции преобразователя tr ;
•переходная характеристика преобразователя h(t).

100
Систематическая составляющая погрешности средства измерений (СИ)- составляющая погрешности данного экземпляра СИ, при одном и том же значении измеряемой или воспроизводимой величины в неизменных условиях применения СИ остающаяся постоянной или изменяющаяся настолько медленно, что ее изменениями за время проведения измерения можно пренебречь.
Случайная составляющая погрешности СИ, случайная погрешность обусловленная только свойствами самого СИ; представляет собой центрированную случайную величину или центрированный случайный процесс.
Случайная составляющая погрешности от гистерезиса СИ – случайная составляющая погрешности СИ, обусловленная различием функций преобразования данного экземпляра прибора, или различием зависимостей показаний данного экземпляра прибора от информативного параметра входного сигнала при различных направлениях его изменения.
Функция влияния - зависимость изменения метрологической характеристики СИ от изменения влияющей величины или от изменения совокупности влияющих величин.
Динамическая характеристика СИ – метрологические характеристики свойств СИ, проявляющихся в том, что на выходной сигнал этого СИ влияют значения изменения входного сигнала во времени.
Переходная характеристика СИвременная характеристика СИ, полученная при ступенчатом изменении входного сигнала.
Импульсная переходная характеристика СИвременная характеристика СИ, получаемая при приложении ко входу СИ входного сигнала в виде дельта функции (функции Дирака)
Амплитудно - частотная характеристика СИ - зависящее от частоты отношение амплитуды выходного сигнала линейного СИ в установившемся режиме к амплитуде входного гармонического сигнала.
Минимально-фазовые СИсредства измерений, фазо-частотная и амплитудночастотная характеристики которого однозначно функционально взаимосвязаны.
Передаточная функция СИотношение преобразования Лапласа выходного сигнала линейного средства измерений к преобразованию Лапласа входного сигнала при нулевых начальных условиях.
Время реакции СИвремя установления показаний (для показывающего прибора), время установления выходного сигнала для измерительного преобразователя.
Погрешность датирования отсчета аналого-цифрового преобразователя или цифрового измерительного прибораслучайная величинаинтервал времени, начинающийся в момент начала цикла преобразования (запуска) АЦП или ЦИП и заканчивающийся в тот момент, когда значение изменяющейся величины и значение выходного цифрового сигнала на данном цикле преобразования оказались равны.
101
3.4.4. Способы нормирования метрологических характеристик
Типовые характеристики, предназначенные для определения результатов измерений, нормируют как номинальные характеристики средств измерений данного типа.
Для конкретных экземпляров средств измерений, предназначенных для применения с одной или несколькими индивидуальными характеристиками, а не номинальными, распространяющимися на все экземпляры средств измерений данного типа, соответствующие номинальные характеристики можно не нормировать. В этих случаях нормируют пределы (граничные значения), в которых должна находиться индивидуальная характеристика при предусмотренных условиях применения средств измерений.
Характеристики систематической составляющей погрешности средств измерений нормируют путем установления:
• |
пределов (положительного и отрицательного) SP допускаемой систематической |
составляющей погрешности средств измерений данного типа или |
|
• |
пределов SP допускаемой систематической составляющей погрешности, |
• |
математического ожидания M [ S ] и среднего квадратического отклонения |
σ[ |
S ] систематической составляющей погрешности измерений данного типа. |
Характеристики случайной составляющей погрешности нормируют путем установления:
• |
предела |
o |
допускаемого |
среднего |
квадратического |
отклонения |
случайной |
|
σP |
|
|||||||
|
|
|
|
|
|
|
|
|
составляющей погрешности средств измерения данного типа или |
|
|
||||||
• |
предела |
o |
допускаемого |
среднего |
квадартического |
отклонения |
случайной |
|
σP |
|
|||||||
|
|
|
|
|
|
|
|
|
составляющей погрешности, номинальной нормализованной автокорреляционной |
||||
функции ro |
(τ ) |
или номинальной функции спектральной плотности S o |
(ω) |
случайной |
|
sf |
|
SP |
|
составляющей погрешности и пределов допускаемых отклонений этих функций от номинальных.
|
Характеристику случайной составляющей |
o |
|
H погрешности от гистерезиса |
|
нормируют путем установления (без учета знака) |
H P допускаемой вариации выходного |
|
сигнала (показания) средства измерений данного типа. |
||
|
Функции влияния нормируют путем установления: номинальной функции влияния |
|
ψ |
(ξ) и пределов допускаемых отклонений от нее или граничных функций влияния |
|
|
sf |
|
верхней ψ (ξ) и нижней ψ (ξ).
Граничные функции влияния нормируют для таких средств измерений, у которых велик разброс функций влияния по множеству экземпляров. В силу этого номинальную
102
характеристику влияния не нормируют. При применении таких средств измерений, в случае необходимости, определяют функции влияния, индивидуальные для каждого экземпляра средств измерений. Нормированные граничные функции влияния используют для контроля за качеством средств измерений.
Изменения значений МХ, вызванные изменениями влияющих величин, нормируют путем установления пределов (положительного и отрицательного) допускаемых изменений характеристики при изменении влияющей величины в заданных пределах. Функции влияния и наибольшие допускаемые изменения параметров нормируют отдельно для каждой влияющей величины.
3.4.5.Формы представления нормированных метрологических характеристик.
Номинальную функцию преобразования измерительного преобразователя представляют в виде формулы, таблицы или графика. Номинальные значения однозначной или многозначной меры выражаются именованными числами.
Нормированные характеристики погрешности средств измерений представляют числом или функцией информативного параметра входного и выходного сигнала для абсолютных, относительных или приведенных погрешностей.
Нормированный предел H P допускаемой вариации средств измерений представляют числом в единицах измеряемой величины или процентах нормирующего значения.
Номинальные функции автокорреляции, спектральной плотности, функции или плотности распределения систематической и случайной составляющих погрешности средств измерений представляют в виде формулы, таблицы, графика. Пределы допускаемых изменений метрологических характеристик представляют в виде границ зоны вокруг действительного значения данной МХ при нормальных условиях.
103
3.4.6. Возможность расчета погрешностей средств измерений в реальных условиях эксплуатации.
Рассмотренный подход к оценке метрологических характеристик СИ в виде комплекса, позволяет решить вопрос о расчете погрешности СИ в реальных условиях эксплуатации. За последнее время в этом возникла серьёзная необходимость.
Погрешность измерений обусловлена в общем случае рядом факторов. Прежде всего, она зависит от свойств применяемых средств измерений - значения инструментальной погрешности измерений, а также способов применения средств измеренийметодик выполнения измерений, условия в которых производятся измерения, и ряда других факторов. В связи с автоматизацией процессов измерений на предприятиях связи усложняются условия эксплуатации и повышаются скорости измерений. Изменения окружающей среды часто являются факторами, влияющими на погрешность измерений. В этих условиях оценка инструментальной составляющей погрешности измерений в реальных условиях применения средства измерений оказывается сложной. Она может производится только на основании информации о свойствах средств измерений - метрологических характеристик (МХ), характере измерений влияющих величин и свойств объекта измерений, определяющих его реакцию при подключении средств измерений.
Сведения о МХ, как правило, содержатся в эксплуатационной документации. Лишь в случаях, когда данных о нормированных типовых МХ недостаточно для эффективного использования средств измерений, экспериментально исследуют конкретные экземпляры средств измерений для определения индивидуальных МХ. Согласно ГОСТ 8.009-84 в эксплуатационной документации для конкретных типов средств измерений установлены соответствующие комплексы нормируемых метрологических характеристик (НМХ).
Инструментальная составляющая при этом представляется в виде ряда составляющих, обусловленных отдельными метрологическими свойствами средств измерений. Принято выделять четыре составляющие:
•основную погрешность, обусловленную не идеальностью собственных свойств средств измерений, т.е. отличием в нормальных условиях действительных характеристик от номинальных характеристик;
•дополнительную погрешность, вызванную реакцией средств измерений на изменения внешних влияющих величин и неинформативных параметров входного сигнала относительно их нормальных значений;
104
•динамическую погрешность, обусловленную реакцией средства измерений на скорость (частоту) изменения входного сигнала;
•погрешность взаимодействия, связанную с возможным изменением значения измеряемой величины относительно того значения, которое имела измеряемая величина до подключения средства измерений к объекту измерений и определение которого является целью измерений.
Указанные составляющие - случайные величины и инструментальная составляющая
погрешности измерений по ГОСТ 8.009-84 - определяется как статистическая (объединение) сумма составляющих. Это важно учитывать, поскольку во всех научнотехнических документах (НТД) до введения этого стандарта НМХ указывались лишь в виде пределов допускаемых значений некоторых отдельных составляющих погрешности. Такому способу задания НМХ соответствовало только арифметическое суммирование, что приводила к заведомо повышенной оценке погрешности. Поэтому принципиальной особенностью регламентированных в ГОСТ 8.009-84 групп НМХ явилось то, что они позволили определить не только математически строгие, но и приближенные, при этом достаточно достоверные для технических измерений оценки инструментальной составляющей погрешности измерений в реальных условиях применения средства измерений. Это существенно, так как требуемая точность даже эксплуатационных измерений согласно ГОСТ 21655-87 ”Каналы и тракты магистральной первичной сети единой автоматизированной системы связи. Электрические параметры и методы измерений” настолько высоки, что выбор подходящих рабочих средств измерений уже становится затруднительным. Более корректная оценка точности измерений по существу стала важным резервом средств измерений.
При выборе методов и средств измерений, обеспечивающих заданные нормы точности, рекомендуется пользоваться методическими указаниями РД 50-453-84 “Характеристики погрешности средств измерений в реальных условиях эксплуатации”. В них установлены методы расчета характеристик составляющей погрешности прямых однократных измерений в соответствии с ГОСТ-8.009-84, а также по известным характеристикам влияющих величин и входного сигнала. Ниже даны рекомендации по применению принятых методов расчета, возможности их реализации и примеры их использования для получения расчетной оценки погрешности средства измерений в конкретных условиях эксплуатации.
105
Нормирование МХ средств измерений конкретного типа осуществляется на основании двух возможных моделей их погрешности в реальных условиях применения- с существенной и несущественной случайными составляющими основной погрешности ( так называемые модели 1 и 2).
3.4.7. Первый метод расчета погрешности средства измерений в реальных условиях эксплуатации.
Первый метод дает вероятностную оценку погрешности СИ и основан на использовании так называемой модели 1, которая заключается в статистическом объединении характеристик пяти составляющих погрешностей СИ и составляющей int ,
обусловленной взаимодействием СИ с объектом измерений: |
int |
|
|
||||||||||
( |
M1 )1 = |
|
o |
l |
|
|
|
|
|
|
|
|
|
OS |
0 |
OH ∑ |
ci |
|
dyn |
|
int |
, |
(3.21) |
|
|
||
|
|
|
|
i = 1 |
|
|
|
|
|
|
|||
где OS - |
систематическая |
составляющая |
основной погрешности; |
O - |
случайная |
||||||||
составляющая |
основной |
погрешности; |
OH - |
случайная |
составляющая |
основной |
|||||||
погрешности, обусловленная гистерезисом; |
|
|
|
|
|
|
|
||||||
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ ci - |
объединение дополнительных погрешностей средств измерений, |
обусловленных |
|||||||||||
i=1
действием влияющих величин и неинформативных параметров входного сигнала средства измерений; l- число учитываемых дополнительных погрешностей OS .
Исходные данные для расчета первым методом.
Нормируемые МХ средства измерений:
математическое |
ожидание M [ |
OS ] и среднее квадратическое отклонение σ[ ]OS |
|||
систематической |
составляющей |
основной погрешности; предел |
o |
|
допускаемого |
σP |
o |
||||
|
|
|
|
|
|
среднего квадратического отклонения случайной составляющей основной погрешности;
предел HOP допускаемой вариации средства измерений при нормальных условиях,
|
|
|
|
|
|
106 |
номинальная цена μsf |
единицы наименьшего разряда кода цифрового измерительного |
|||||
прибора; номинальная функция влияния |
|
|||||
ψ s.sf |
(ξ j ) , |
j=1,2…..,n на систематическую составляющую; |
|
|||
ψσsf |
(ξj ), |
j=1,2……, l |
на среднее квадратическое отклонение случайной составляющей |
|||
и ψ н.sf (ξ j |
), |
j=1,2…….,к |
на вариацию средства |
измерений; одна из полных |
||
динамических |
характеристик: |
номинальная переходная |
hsf (t), импульсная gsf (t), |
|||
амплитудно-фазовая характеристикаGsf (jω), номинальная передаточная функцияGsf (S ).
Характеристики влияющих величинξ j :
значения влияющих величин ξ j (j =1,2…n) или математическое ожидание M [ξ j ], среднее
квадратическое отклонение σ[ξ j ], наименьшееξнj и наибольшееξвj значения, соответствующие реальным условиям применения средства измерения, j=1,2……, n(l,к).
Характеристики входного сигнала х:
спектральная плотность Sx (ω) или автокорреляционная функция Rx (τ ) входного сигнала средства измерений.
3.4.8. Основные соотношения при расчете погрешности СИ в реальных условиях эксплуатации по первому методу.
Первый метод расчета погрешности средства измерений в реальных условиях применения включает определение статистических моментов составляющих погрешности средства измерений. Сведения же о законах и параметрах распределения влияющих величин в инженерной практике, как правило, отсутствуют. Для рассмотрения примера расчета положим, что характеристики влияющих величин заданы, а функции влияния являются линейными
107
ψs.sf (ξ j )= Ks.sfj (ξj −ξref . j ). |
(3.22) |
В формуле ψs.sf (ξ j )- функция влияния определенного фактора (j), например
напряжения питания прибора, на конкретную составляющую погрешности, например
величину измеренного напряжения. Величина K - коэффициент пропорциональности ,
а величины в скобкахξj иξref . j - разность между реальным значением параметра (в
рассматриваемом случае напряжения питания прибора), и его номинальным значением.
Математическое ожидание статической составляющей погрешности в общем случае вычисляется по формуле
M [ ξ]= M [ os]+ ∑n ψs.sfj (ξ j ). |
(3.23) |
j=1 |
|
Здесь суммирование выполняется для n влияющих величин, значения которых в момент измерения отличаются от нормальных, установленных для данного средства измерений.
Дисперсия статической составляющей:
D |
[ |
ξ]= |
σ |
2[ os]+ |
|
o |
+∑l ψ |
(ξ ) |
2 + |
|
1 |
|
|
H |
op +∑k ψ |
(ξ ) |
2 + |
μ2sf |
(3.24) |
|||
p |
|
o |
12 |
12 |
||||||||||||||||||
|
|
|
|
j=1 |
σsf j |
|
|
|
j=1 |
Hsf j |
|
|
|
|||||||||
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где l, к – числа учитываемых влияющих величин на среднее квадратическое отклонение случайной составляющей погрешности и вариацию средств измерений. Величина μsf2 -
номинальнапя цена единицы наименьшего разряда кода цифрового измерительного прибора. Для аналоговых средств измерений последнее слагаемое равно нулю.
Если нормирован предел OSP (предел систематической составляющей основной погрешности СИ) без указания σ[ os ] и нет оснований предполагать несимметричность и полимодальность распределения систематической составляющей погрешности,
допускается приниматьσ[ os ]= |
SM |
|
3 |
||
|

|
|
|
|
|
108 |
σ[ |
os ]= |
OSP |
(3.25). |
||
3 |
|
||||
|
|
|
|
|
|
В случае средств измерений с индивидуальными НМХ принимается |
|||||
σ[ |
os ]= |
|
SM |
|
(3.26). |
|
3 |
|
|||
|
|
|
|
|
|
В выражении 3.26 SM - наибольшее возможное по абсолютной величине значение
неисключенной систематической составляющей погрешности конкретного экземпляра СИ.
Если для j-ой влияющей величины известны только её наименьшее ξ нj ,
соответствующие реальным условиям эксплуатации, и нет оснований выделить области предпочтительных значений влияющих величин в этих границах, за исключением области вокруг центра интервала, то допускается для расчета характеристик погрешности СИ пользоваться соотношением:
|
|
|
|
ξ |
|
−ξ |
|
|
|
|
|
|
|
вj |
|
|
|
||
|
|
|
|
нj |
|
(3.27) |
|||
σ ξ |
|
= |
|
|
|
|
|
. |
|
|
|
|
|
2 |
3 |
|
|
|
|
|
j |
|
|
|
|
|
|
Пример расчета погрешности средства измерений в реальных условиях эксплуатации.
Милливольтметр имеет следующие данные:
•Нормируемые метрологические характеристики:
•Предел систематической составляющей погрешности OSP = 10 мВ; предел допускаемого среднего квадратического отклонения случайной составляющей основной погрешности данного экземпляра прибора σP o = 5 мВ; предел
допускаемой вариации (гистерезиса) прибора при нормальных условиях Нор= 6 мВ.
•Функция влияния температуры и напряжения питания номинальные
•ψs.sf (ξ1 )= Ks.sf1 (ξ1 −ξref1 );
109
• |
ψs.sf (ξ2 )= Ks.sf2 (ξ2 −ξref 2 ); |
• |
ψσ.sf (ξ1 )= Kσ.sf1 (ξ1 −ξref1 ); |
•ψσ .sf (ξ2 )= Kσ .sf2 (ξ2 −ξref 2 )
где Ks.sf1 (ξ1 )=0,5 мВ/ о С; Ks.sf2 (ξ2 )= 0,4 мВ/B; Kσ.sf1 (ξ1 )=0,1 мВ/ о С, а
Kσ.sf2 (ξ2 )= 0,1 мВ/В.
Номинальные значения влияющих величин ξref1 = 20 о С и ξref2 = 220 В.
•Характеристики влияющих величин:
влияние температуры в пределах: ξн1 = 25о С; ξв1 = 35 О С ;
влияние изменения напряжения питания в пределах: ξн2 = 200 В; ξв2 =230 В.
Решение.
Поскольку по условиям задачи нет указаний на несимметричность распределения влияющих величин будем считать, что математическое ожидание систематической составляющей погрешностиM [ ]os = 0 , а математическое ожидание влияющих величин соответствует срединам интервалов, т.е.
М[ξ1 ]=0,5(ξн1 +ξв1 )=0,5(25 +35) = 30oС ,
М[ξ2 ]= 0,5(ξн2 + ξв2 )= 0,5(200 + 230) = 215 В.
Всоответствии с формулой 3.4.3. имеем:
M [ ξ ]= M [ os ]+Ks.sf1 (M [ξ1 ]−ξref .1 )+ Ks.sf2 (M [ξ2 ]−ξref .2 )= 5 −2 = 3мВ
Дисперсия D [ ξ ] статической составляющей погрешности СИ для заданных характеристик влияющих величин вычисляется по формуле 3.24.
D[ ξ]=σ2[ os]+[σp[&0]+Kσ.sf1(ξв1 −ξref1)+Kσsf2(ξн2−ξref.2)]2 +Ks.sf12σ2[ξ1]+ +Ks.sf22 σ2[ξ2]+Hop2 /12.
Для случая, когда нет оснований выделить область предпочтительных значений
110
систематической составляющей основной погрешности в интервале(− OSP , OSP )
и области предпочтительных значений влияющих величин в заданных интервалах, на основании 3.25 и 3.27 имеем:
D[ os ]= |
|
2 osp |
= |
|
100 |
= 33,3 мВ2 |
; |
|
|
||||||
|
3 |
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σ[ξ1 |
]= |
ξВ1 −ξН1 |
|
|
= 2,9oС ; |
|
|
|
|||||||
|
|
|
|
||||||||||||
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
σ[ξ2 |
]= ξВ2 −ξН2 |
= |
|
230 −200 |
=8,7 В. |
|
|
||||||||
|
|
|
|
||||||||||||
|
2 |
3 |
|
|
|
|
2 |
3 |
|
|
|
|
|||
С учетом полученных значений средних квадратических отклонений |
|
||||||||||||||
D[ ξ ]= 33,3 + (5 +1,5 + 2)2 |
+ 0,25 2,92 |
+ 0,16 8,7 |
2 + |
6 2 |
= 123 мВ2 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
3.4.9. Основные соотношения при расчете погрешности СИ в реальных условиях эксплуатации по второму методу.
В основу второго метода расчета погрешности СИ в реальных условиях эксплуатации доверительный интервал, с помощью которого оценивается погрешность вычисляется для доверительной вероятности равной 1.
Нижняя си..н и верхняя си.в границы интервала, в которых с вероятностью Р=1
находится погрешность СИ в реальных условиях эксплуатации, определяется по формулам:
|
|
|
n |
|
|
|
си.в = |
op |
+ ∑ |
сj ; |
(3.28) |
|
|
||||
|
|
|
j =1 |
|
|
|
си.н = − |
си.в , |
|
(3.29) |
|
|
|
|
|||
где предполагается, что отклонение от истинного значения симметричны. В |
|||||
формуле 3.28. |
op |
предел величин допускаемых основных погрешностей, т.е. |
|||
111
погрешностей, возникающих при нормальных условиях эксплуатации, а ci -
дополнительные погрешности. Число n таких составляющих должно быть равно числу всех величин существенно влияющих на погрешность СИ в реальных условиях эксплуатации. Сумма этих составляющих определяет дополнительную погрешность СИ, возникающую при выходе условий эксплуатации прибора из нормальных условий. Второй способ расчета погрешности СИ в реальных условиях эксплуатации применим только в тех случаях, когда случайная составляющая основной погрешности может считаться пренебрежимо малой.
Следует обратить внимание на то, что если положить в формуле 3.28 сумму дополнительных погрешностей равной нулю (что будет соответствовать нормальным условиям эксплуатации СИ), то границы погрешности определяются пределом основной погрешности, т.е. в данном случае мы приходим к нормированию погрешностей СИ таким способом, который характерен при использовании классов точности.
•В данном случае рассчитанный интервал погрешности будет представлять собой грубую оценку сверху искомой инструментальной погрешности, охватывающую все возможные, в том числе редко реализующиеся, значения погрешностей. Для подавляющего большинства измерений этот интервал будет существенно превышать интервал, в котором будут действительно находиться инструментальные составляющие погрешности измерений. Условие, что вероятность, с которой погрешность находится в данном интервале, должна быть равна единице, практически приводит к существенно завышенным требованиям к метрологическим характеристикам СИ при требуемой точности измерений.
Пример расчёта по второму методу.
Исходные данные.
Нормируемые метрологические характеристики СИ:
• предел допускаемой основной погрешности милливольтметра op = 20 мВ ;
•наибольшее допускаемое изменение p ( ξ1 ) погрешности, вызванное изменением температуры от нормального значения 20o С , составляет 5 мВ на каждые 10o
отклонения температуры;
112
•наибольшее допускаемое изменение p ( ξ2 ) погрешности , вызванное изменением напряжения питания от нормального значения 220 В, составляет 10 мВ при отклонении напряжения на ±10% ;
•пределы изменения влияющих величин :
•ξн1 =25oС, ξв1 =35o С, ξн2 =200В,ξв2 =230В.
Решение.
Наибольшее значение возможных дополнительных погрешностей, связанных с изменением температуры и питающего напряжения определим по формулам:
с1m |
= p (ξ1 ) |
ξв1 −ξref .1 |
= 5 |
(35 − 20) |
=7,5 мВ; |
||
ξ 1 |
|
10 |
|||||
|
|
|
|
|
|||
с2m |
= p (ξ2 ) K (ξ2 )= 10 |
230 − 220 |
100 = 4,5 мВ. |
||||
10 220 |
|||||||
|
|
|
|
|
|
||
|
При определении |
с1m |
учитывается , что возможный диапазон изменения |
||||
температуры лежит выше номинального значения, равного 200 С, поэтому в формулу в числитель поставлена цифра 35, соответствующая максимуму температуры. Величина 10, поставленная в знаменатель, позволяет вычислить относительное изменение температуры, 5 мВ, соответствует чувствительности прибора к изменению температуры, данной в условиях задачи.
Во второй формуле p(ξ2 ) отклонение в показаниях прибора , равное 10 мВ на
каждые±10% изменения напряжения питания, а K (ξ2 ), отношение процентного изменения напряжения питания (230-220) относительно номинального значения в 220 В, к 10%, для которых дана величина p(ξ2 ).
Нижняя си.н и верхняя границы си.в границы интервала, в котором с вероятностью Р=1 находится погрешность СИ, вычисляется по формулам:
113
си.н = − ( |
op + c1m + c2m )= −(20 +7,5 + 4,5)= − 22 мВ, |
си.в =− |
си.н = 22 мВ. |
114
Глава 4. Аналоговые электромеханические измерительные приборы.
4.1. Общие сведения и классификация
Аналоговыми называют приборы, показания которых являются непрерывной функцией изменений измеряемой величины. Стрелочные аналоговые приборы содержат отсчетное устройство, состоящее из шкалы и указателя, и измерительный механизм. Измерительный механизм воспринимает энергию измеряемого сигнала и преобразует ее в угловое перемещение некоторой подвижной части, жестко связанной с указателем. Для перемещения подвижной части необходимо, чтобы на нее действовал вращающий момент. Если на подвижную часть никакие другие силы не действуют, то она отклонится настолько, сколько допускает конструкция. Отклонение будет максимальным независимо от величины вращающего момента. Что бы каждому значению вращающего момента соответствовало свое отклонение подвижной части, необходим противодействующий момент, направленный навстречу вращающему моменту и возрастающий по мере увеличение угла поворота. Обычно такой противодействующий момент создается одной или двумя спиральными пружинами, которые при повороте подвижной части закручиваются (или раскручиваются). Подвижная часть поворачивается до тех пор, пока возрастающий противодействующий момент не окажется равным вращающему моменту. При необходимости пружины служат для подвода тока к подвижной части прибора. Часто противодействующий момент создается упругими растяжками, на которых подвешивается подвижная часть.
Наличие подвижной части в измерительных механизмах вызывает необходимость в специальных опорных устройствах, создающих возможно меньший момент трения. Момент трения отсутствует в приборах, в которых подвижная часть укреплена на растяжках.
В процессе движения к положению равновесия подвижная часть, накопив некоторую кинетическую энергию, по инерции проходит это положение, а затем начинает совершать колебания. Если не принимать специальных мер, время, необходимое для установления отклонения, становится недопустимо большим. Для уменьшения времени успокоения используются специальные устройства - успокоители.
114
115
Они строятся так, чтобы момент успокоения возникал лишь при движении подвижной части.
Основные технические требования, которым должны удовлетворять электроизмерительные приборы, сформулированы в ГОСТ 22261-76. Имеются стандарты на отдельные элементы приборов. Например, ГОСТ 9444-74 посвящен растяжкам и подвесам, ГОСТ 23217-78 — условным обозначениям, наносимым на приборы. Технические требования охватывают все метрологические характеристики (пределы допускаемых основных и дополнительных погрешностей, дену деления шкалы, конечные значения диапазонов измерений, время установления показаний и т.д.), методы испытаний, правила приемки. Классы точности также нормируются стандартами. Например, ГОСТ 8711-78 устанавливает следующие классы точности на амперметры и вольтметры; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4; 5. Значительный объем информации о принципе действия прибора, возможной предельной погрешности, условий работы может быть извлечен из условных обозначений, нанесенных на циферблат прибора. Условные обозначения, отражающие принцип действия прибора, показаны в таблице 4.1.
Условные обозначения, наносимые на электроизмерительные аналоговые приборы нормированы ГОСТ 23217-78. Этот стандарт полностью соответствует Публикации МЭК 51. Международная электротехническая комиссия рекомендовала так же обозначения основных единиц и их кратных и дольных значений, рода тока, безопасности, используемого положения прибора, класса точности, обозначение принципа действия прибора. Некоторые из этих обозначений приведены в таблице 4.2.
Таблица 4.1.
N |
Тип прибора |
Обозначение принципа |
|||
|
|
действия |
|||
1 |
Магнитоэлектрический прибор с |
|
|
|
|
|
подвижной катушкой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Магнитоэлектрический логометр с |
|
|
|
|
|
подвижными катушками |
|
|
|
|
|
|
|
|
|
|
3 |
Электромагнитный прибор |
|
|
|
|
|
|
|
|
|
|
115
116
|
Таблица 4.1 (продолжение) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
Электродинамический прибор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
Ферродинамический прибор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
Электростатический прибор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
Термопреобразователь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
изолированный |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
Термопреобразователь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неизолированный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.2.
N |
Параметр |
Условное |
|
|
обозначение |
1 |
Класс точности при |
|
|
нормировании приведенной |
1,5 |
|
погрешности, например , 1,5 |
|
|
|
|
2 |
То же, при нормировании |
1,5 |
|
приведенной погрешности в |
|
|
процентах от длины шкалы |
|
3Горизонтальное положение шкалы
4Вертикальное положение
шкалы
5 Наклонное положение шкалы под определенным углом к 600 горизонту, например, 600.
6 |
Направление ориентировки |
N |
|
|
прибора в земном магнитном |
||
|
|
|
|
|
поле |
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
7Измерительная цепь изолирована от корпуса и
испытана напряжением, |
2 |
например 2 кВ |
|
116
117
4.2.Основные элементы аналоговых стрелочных приборов.
Одним из главных элементов аналогового стрелочного прибора является шкала. Шкала является устройством, с помощью которого осуществляется отсчет показаний. Для этого на ее поверхность наносятся отметки в виде коротких линий, интервал между которыми называют делением шкалы. Рис. 4.1. Отметки шкалы, снабженные числами, называют числовыми отметками шкалы. Шкалы могут быть равномерными или неравномерными. Наименьшее значение измеряемой величины указанное на шкале, называют начальным значением шкалы, наибольшее - конечным. Диапазон показаний определяют по начальному и конечному значениям шкалы. Под диапазоном измерений понимают область значений ой величины, для которой нормированы допускаемые погрешности средства измерения. При равномерных шкалах обычно диапазон показаний и диапазон измерений совпадают.
|
|
|
Отметки |
|
|
|
|
|
шкалы |
|
|
Нижний |
-10 |
0 |
10 |
Верхний |
|
предел |
предел |
||||
-20 |
|
20 |
|||
измерения |
|
измерения |
|||
|
|
|
|||
|
-30 |
|
|
30 |
|
|
Деление |
|
|
||
|
шкалы |
|
|
||
Диапазон
измерения
Рис.4.1
На рис.4.1 представлена линейная двухстороння шкала, нуль показаний находится в центре шкалы и прибор позволяет отсчитывать как положительные, так и отрицательные значения величин.
Нелинейная шкала, представлена на рис. 4.2. Как видно из рис. 4.2. расстояние
3 |
4 |
|
2 |
|
|
1 |
5 |
|
0 |
||
|
117 |
Рис.4.2. |
118
между делениями шкалы увеличиваются по мере приближения к верхнему пределу показаний. Такая шкала удобна при отсчете больших значений величин.
0,4 0,6
0,2 |
0,8 |
|
|
mA |
0 |
10 |
Рис.4.3.
Шкала, изображенная на рис. 4.3. называется перегрузочной. Расстояние между большими отметками шкалы одинаковы, однако последний оцифрованный участок шкалы, примыкающий к предельному значению фиксирует увеличение измеряемой величины не на 0,2, как на остальных участках, а от 0,8 до 10. Приборы с такими шкалами обладают способностью обеспечивать удобство отсчета на линейном участке и не «зашкаливаться» при резком увеличении измеряемого сигнала. Перегрузочные амперметры позволяют измерить величины токов при их резких «бросках», возникающих, например, при включении мощных электродвигателей.
Внешний вид типичных стрелочных приборов представлен на рис. 4.4 – 4.8.
V |
75 |
100 |
|
|
50 |
|
|
|
25 |
|
|
1,5 |
0 |
2 |
|
ГОСТ 8.711-60 |
|
||
|
Рис.4.4 |
|
|
118

119
В соответствии нанесенными на лицевую панель прибора условными обозначениями, изображенный на рис. 4.4. прибор – вольтметр магнитоэлектрической системы, с диапазоном измерений от 0 до 100 В, шкала линейная, класс точности 1,5, выполнен в соответствии с ГОСТ 8.711 – 60, измерительная цепь, изолированная от корпуса, испытана напряжением 2 кВ, при работе шкала должна занимать вертикальное положение.
Рис.4.5 |
Рис.4.6 |
|
На рис. 4.5 и 4.6. представлены приборы миллиамперметры магнитоэлектрической системы с линейными шкалами на различные диапазоны измеряемого тока. Прибор на рис.4.5. предназначен для работы в горизонтальном положении, а прибор на рис. 4.6. , имеющий двухстороннюю шкалу, позволяет измерять как положительные так и отрицательные значения тока и должен работать в вертикальном положении.
Рис.4.7 |
Рис.4.8 |
119
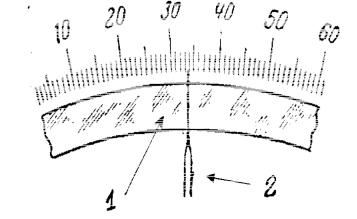
120
На рис. 4.7 изображен внешний вид вольтметра, диапазон показаний не совпадает с диапазоном измерений, который начинается не от нуля, а от 320 В.
Для определения диапазона измерений на шкале таких приборов обычно ставят точки. Если наибольшее значение диапазона измерений и диапазона показаний совпадают, точка ставится только в начальной части шкалы. В диапазоне измерений погрешность определяется по классу точности прибора.
Механический указатель прибора представляет собой стрелку, конец которой выполнен в форме, облегчающей отсчет показаний. Возможные формы стрелок, указаны в ГОСТ 3051-69.
В лабораторных приборах повышенных классов точности применяют отсчетное устройство с зеркальной шкалой. Для этого под шкалой (рис.4.9) устанавливается зеркало 2, При отсчете оператор совмещает стрелку 3 с ее изображением в зеркале. При этом линия наблюдения составляет с плоскостью зеркала угол 90o , что устраняет погрешность отсчета, связанную с параллаксом.
Для удобства отсчета применяются так же приборы со световым указателем. На подвижной части таких приборов крепится зеркальце. Луч света от миниатюрной лампы накаливания отражается от него и образует на матовом стекле световую отметку. При повороте подвижной части поворачивается зеркальце, изменяется угол отражения луча и положение светового пятна относительно шкалы.
Рис.4.9
120

121
Конструкция устройства, создающего противодействующий момент показана на рис.4.10
.
Рис.4.10
Внутренний конец спиральной пружины 1 прикрепляется к подвижной части измерительного механизма 2, а наружный конец к неподвижной части прибора. Противодействующий момент увеличивается по мере закручивания пружины. Для регулировки пружины используется корректор. С помощью эксцентрично расположенного винта 4 регулируется положение поводка 3 и первоначальное натяжение пружины. Нулевой противодействующий момент должен соответствовать нулевому показанию стрелки 5.
Рис. 4.11
На рис. 4.11 показан другой способ получения противодействующего
121
122
момента, основанный на применении растяжек. Растяжки представляют собой металлические ленты толщиной порядка 0,0I мм. Подвижная часть прибора подвешивается на двух растяжках. Растяжки выполнены из металла, обладающего необходимой упругостью. При повороте подвижной рамки прибора, они создают противодействующий момент и одновременно служат для ее крепления. При необходимости по растяжкам может подводиться ток к рамке, которая обычно наматывается изолированным проводом.
Для предотвращения резких отклонений стрелки прибора при подаче сигнала, а так же колебаний стрелки служат успокоители. Колебания стрелки около отметки шкалы, соответствующей подаваемому на вход прибора измерительному сигналу обычно возникают из-за высокой добротности подвижной части прибора, поведение которой можно описать тем же дифференциальным уравнением 2-го порядка, что и электрический колебательный контур. Из теории линейных электрических цепей известно, что колебательный контур можно превратить в апериодический, зашунтировав (демпфировав) его сопротивлением соответствующей величины. Демпфирующие устройства используемые для создания успокаивающего момента в стрелочных приборах имеют разные принципы действия.
На рис.4.11 показан успокоитель магнитоиндукционного типа. Он основан на использовании вихревых токов, возникающих в тонкой алюминиевой пластине 2. При повороте рамки вокруг оси алюминиевая пластина поворачивается перемещаясь в магнитном поле, создаваемым постоянным магнитом 1. Магнитное поле, создаваемое вихревыми токами в алюминиевой пластине, взаимодействуя с полем постоянного магнита, создает успокаивающий момент, который тем больше, чем быстрее поворачивается подвижная часть прибора.
Рис. 4.12
Воздушный успокоитель (рис. 4. 12а) состоит из, камеры 1, внутри которой
122

123
перемешается легкое алюминиевое крыло 2, закрепленное на оси подвижной части механизма 3. Успокаивающий момент возникает благодаря прохождению воздуха через узкий зазор между стенками камеры и крылом. Жидкостный успокоитель (рис. 4.12б) основан на использовании специальной маловысыхающей кремнеорганической жидкости 3, находящейся в зазоре 0,1... 0,3 мм между двумя дисками 1 и 2. Успокаивающий момент возникает при повороте одного диска относительно другого вследствие трения между различными слоями жидкости.
В большинстве случаев момент успокоения связан со скоростью подвижной части линейной зависимостью Mp= p dα/dt, где р-коэффициент пропорциональности (демпфирования), а dα/dt- производная от угла поворота подвижной части во времени, т.е. угловая скорость перемещения подвижной части.
α MP<MK 1
2  MP>MK
MP>MK
MP=MK
3
t
Рис. 4.13
На рис 4.13 показаны графики, характеризующие движение подвижной части прибора во времени для трех случаев: момент успокоения меньше критического Мк (кривая 1), равен критическому и больше критического (кривые 2 и 3). Согласно ГОСТ 22261-76 время успокоения не должно превышать 4 с.
Последним элементом общим для большинства приборов стрелочного типа является устройство для крепления оси подвижной части. В том случае, когда оно крепится не на растяжках, как это было показано на рис. 4.11, ось подвижной части оканчивается керном. Керн (рис. 4.14) выполняется из специального сплава, его конец закруглен и отполирован. Керн опирается на подпятник, который выполняется из твердых материалов (агата или корунда).
123
124
Рис. 4.14.
Подпятник закрепляется в металлической оправе, которая соединяется с подвижной частью прибора с помощью резьбы, позволяющей так отрегулировать положение подпятника, что исключить осевой люфт подвижной части прибора.
4.3. Магнитоэлектрическиеизмерительныемеханизмы.
Конструкция прибора магнитоэлектрической системы показана рис. 4.15. Между полюсами постоянного магнита N и S расположены полюсные наконечники с цилиндрической расточкой. Магнитное поле замыкается через сердечник «1» цилиндрической формы, выполненный из магнитомягкого материала и укрепленный неподвижно с помощью специальной латунной накладки не показанной на рисунке. В кольцевом зазоре между наконечниками сердечником создается равномерное магнитное поле. В этом же зазоре расположена подвижная катушка (рамка 2), выполненная из изолированной медной проволоки. Проволока либо навивается на алюминиевый каркас, либо скрепляется клеем. К рамке с двух
сторон |
приклеиваются |
алюминиевые |
буксы для крепления растяжек или |
|
кернов. |
Стрелка |
и |
вся подвижная |
часть механизма уравновешиваются |
грузиками, играющими роль противовеса. |
|
|||
Для регулировки магнитного поля в зазоре (рис.4.16.) просмотрен шунт (МШ), выполненный из магнитомягкого материала, по которому замыкается часть магнитного потока. На рис.4.16 сердечник обозначен буквой а, зазор обозначен
124
125
буквой А и F- вектор силы, образующий вращающий момент.
Ток к рамке подводится по спиральным пружинам и растяжкам. Возникающий вращающий момент
(4.1).
где B- индукция в зазоре; s— площадь рамки; w- число витков; I— ток,
протекающий по обмотке рамки.
Установившееся отклонение от подвижной части определятся равенством
M = M пр =Wα , где M пр — противодействующий момент; α— угол поворота
подвижной части ; W — коэффициент, зависящий от свойств упругого элемента и называемый удельным противодействующим моментом. Противодействующий момент линейно зависит от угла подвижной части. При M== —М пр имеем BswI = αW .
Откуда : |
α = |
Bsw |
I = SI I . |
(4.2) |
|
||||
|
|
W |
|
|
Выражение |
4.2 |
представляет собой |
уравнение преобразования, где SI |
|
характеризует чувствительность прибора.
Рис. 4.15
125
F
126
МШ
N |
Рис. 4.16. |
S |
|
|
|
|
a |
|
|
A |
Рис.4.16 |
F
Из (4.2.) следует, что угол отклонения пропорционален току, т. е. прибор имеет линейную шкалу. Это одна из особенностей магнитоэлектрических приборов. На рис. 4.3.3. схематически показано прохождение тока по цепям. Ток I от входного
Рис.4.17.
зажима проходит через спиральную пружину и многократно (в зависимости от количества витков провода) обходит рамку. Далее по второй спиральной пружине изолированной от оси и первой пружины, ток поступает на выходной зажим и покидает прибор. В результате прохождения тока образуется магнитной поле, индукция которого обозначена на рис. 4.17. через В. Направлен вектор В перпендикулярно плоскости рамки. На рис. 4.16. Показано направление магнитных силовых линий в зазоре между полюсными наконечниками постоянного магнита и круглым сердечником. Это поле, создаваемое постоянным магнитом параллельно
126
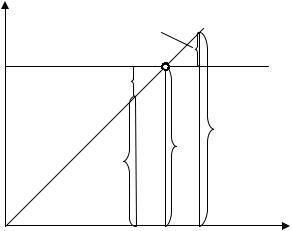
127
плоскости рамки. В тоже время как поле создаваемое током, протекающим через рамку перпендикулярно этой плоскости. В результате взаимодействия двух магнитных полей образуется вращающий момент, стремящийся так повернуть рамку, что бы направление силовых линий рамки и постоянного магнита совпадали. Векторы силы обозначены на рис. 4.16. и 4.17 буквой F. Направление этого вектора зависит от взаимного положения северного и южного полюсов постоянного магнита и направления тока в подвижной рамке. Обычно принято конструировать стрелочные аналоговые приборы таким образом, что бы подвижная часть отклонялась по направлению часовой стрелки. В приборе магнитоэлектрической системы это достигается соответствующим направлением намотки рамки и намагничиванием постоянного магнита. Таким образом, прибор данного типа является полярным. При подключении его к внешней цепи следует соблюдать полярность + и − , в соответствии с обозначениями на его корпусе.
Как следует из выражения 4.2. при отклонении на угол α подвижная часть прибора находится в равновесии. Равновесие достигается когдаM = M пр =Wα .Здесь имеет место особое свойство пружин (или растяжек) создающих противодействующий момент. Как видно из приведенной выше формулы Мпр не является постоянным, а увеличивается пропорционально углу поворота.
М
Мтр |
|
Мпр |
|
А |
|
Мтр |
|
Мвр |
|
|
|
|
|
М пр2 |
|
|
Мпр |
М пр1 |
|
|
|
|
α |
α1 |
α |
α2 |
Рис.4.18 |
||
Изменение моментов вращения и противодействия показаны на рис. 4.18. На
127
128
данном рисунке показано, что вращающий момент Мвр не зависит от угла поворота
(что соответствует 4.1.). Противодействующий момент Мпр , в соответствии со свойствами пружин или растяжек, линейно увеличивается с поворотом подвижной части механизма. В точке А достигается равновесие, которое в идеальном случае соответствует показанию прибора. Реально, в опорах подвижной части имеется трение. Из-за трения при подаче измерительного сигнала на вход прибора угол поворота изменяется от нуля до некоторого значения α1 , т.е. стрелка несколько не доходит до истинного значения. В этом случае противодействующий момент, который соответствует вращающему моменту, складывается из Мпр.1 и момента трения - Мтр.
Аналогично, при уменьшении измеряемой величины, до значения, которому соответствует угол α подвижная часть займет положение α2, т.е стрелка остановится несколько правее той точки шкалы, которой соответствует измеряемая величина.
Таким образом, в приборе возникает погрешность показаний, определяемая моментом трения. Эта погрешность зависит от веса подвижной части, от материала и качества обработки подпятников и кернов, от состояния трущихся поверхностей. Рассмотренное явление называют вариацией показаний прибора или гистерезисом и свойственно не только приборам магнитоэлектрической системы.
Из рис. 4.15. и последующих рисунков остается неясным наличие успокоителя. В явном виде его действительно нет. Роль успокоителя в рассмотренной конструкции прибора выполняет вращающаяся рамка, но не ее обмотка, а алюминиевый каркас, который служит для скрепления проводов и приданию всей конструкции необходимой жесткости. Принцип действия успокоителя аналогичен рассмотренному ранее на рис. 4.11. Образование тормозящего момента с помощью каркаса рамки поясняется на рис. 4.19.
FT 
 В
В
FT
i i
128 |
Рис.4.19 |
|

129
При вращении рамки, представляющей собой замкнутый контур, в магнитном поле В, направление которого показано на рисунке стрелкой, в рамке наводится ток i.
Ток, протекающий по рамке, создает магнитное поле перпендикулярное плоскости рамки. Взаимодействие наведенного поля и постоянного поля магнита создает силу торможения FT направленную встречно направлению движения. Чем быстрее поворачивается рамка, тем больше сила торможения.
При прохождении через рамку переменного тока I вращающий момент М =
ВiSw будет изменяться пропорционально току. Вследствие значительной инерционности подвижной части прибора при достаточно большом периоде колебаний угол поворота
подвижной части будет |
определяться |
средним за период |
значением вращающего |
||||
момента: |
|
|
|
|
|
|
|
Мср = |
|
1 |
Т∫Мdt = |
1 |
ВSwT∫idt = BSwICР |
(4.3.). |
|
|
|
Т |
|||||
|
|
Т 0 |
|
0 |
|
||
Магнитоэлектрические механизмы обычно работают на постоянном токе. Если колебание имеет синусоидальную форму, то среднее значение вращающего момента равно нулю:
M ср = |
Im Bsw |
T∫sinωt dt = 0 |
|
||
|
T o |
|
Принципы построения магнитоэлектрических приборов используются в гальванометрах - высокочувствительных приборах, предназначенных для измерения малых токов (до 10-8 А) и напряжений (до 10-9 В). Гальванометр не имеет градуированной шкалы и цена деления определяется при измерениях, Для получения высокой чувствительности подвижная часть гальванометра крепится на растяжках, что позволяет исключить трение. Для удобства определения показаний применяется оптическая система, состоящая из зеркала и источника света. Отразившийся от зеркала луч достигает экрана и образует отметку, с помощью которой осуществляется считывание показаний.
Приборы магнитоэлектрической системы имеют высокую чувствительность. Удается сконструировать приборы с отклонением на всю шкалу при токе 0,01 мкА. Высокая чувствительность объясняется концентрацией магнитного поля магнита в узком зазоре, из-за чего индукция получается большой. Сильное магнитное поле в
129
130
зазоре делает слабым влияние внешних полей на показания прибора. При использовании магнитных экранов погрешность из-за внешних полей можно свести до десятых долей процента. Потребление тока от внешней цепи приборами магнитоэлектрической системы очень мало, что позволяет снизить потребляемую мощность до 10-9 ВТ.
Магнитоэлектрические приборы относятся к числу высокоточных приборов с классом точности 0,2; 0,1 и даже 0,06. Для достижения высокой точности применяются специальные приемы: искусственное старение магнита, термокомпенсация и т. п. К недостаткам приборов магнитоэлектрической системы относятся чувствительность к перегрузкам (ток протекает по рамке из тонкого провода), сложность и относительно высокая стоимость.
4.4.Электродинамические приборы.
Вприборах электродинамической системы вместо постоянного магнита имеются две неподвижные катушки. Подвижная катушка: 1 (рис. 4.4.1), может поворачиваться относительно неподвижной 2, состоящей из двух частей, разделенных зазором. Разделение неподвижной катушки на две части используется для создания более равномерного магнитного поля в той области пространства, где находится
В1 1
2
i
 В2
В2
3
Рис. 4. 20.
подвижная катушка. Магнитное поле обоих катушек замыкается по воздуху. Направления векторов магнитной индукции В1 –неподвижной катушки (2) и В2 –
130
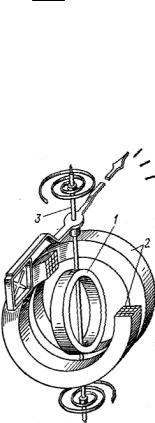
131
подвижной катушки (1) составляют между собой угол. Образующийся вращающий момент перемещает стрелку, укрепленную на оси, относительно шкалы. Конструкция прибора электродинамической системы представлена на рис.4.4.2. Катушка 1 укреплена на оси 3 . Ток к подвижной катушке подается через спиральные пружины, которые одновременно служат для создания противодействующего момента. Неподвижная катушка 2 крепится к корпусу прибора. Успокоитель — воздушного типа. Для увеличения вращающего момента иногда применяют магнитопроводы. Такие приборы называются ферродинамическими. Вращающий момент находится с помощью уравнения Лагранжа:
M = |
∂WM |
, |
(4.4) |
∂α |
где WM -энергия магнитного поля; α—угол отклонения подвижной механизма. Как следует из (4.4), вращающий, момент равен производной от энергии системы по углу
α. Энергия системы, состоящей катушек 1 и 2 с токами i1 и i2 определяется
Рис. 4.21.
соотношением, |
W |
M |
= 1 / 2 L i2 |
+1/ 2 L i |
2 |
+ M 2 |
i i |
2 |
, |
где |
L |
и |
|||
|
|
|
1 |
1 |
2 |
2 |
1 |
1 |
|
|
1 |
|
|||
L2 индуктивности |
катушек, |
|
а |
M12 - |
|
взаимоиндуктивность. |
|
При |
|||||||
дифференцировании учитываем, что токи i1 и i2, |
а также индуктивности |
L1 и |
L2 |
||||||||||||
131

132
постоянны. Лишь M12 зависит от угла поворота α. Следовательно,
M = |
∂W |
= i1 i2 |
∂M 12 |
(4.5.) |
∂α |
∂α |
Если пропустить по катушкам переменные токиi1 и i2, подвижная часть прибора будет реагироватьлишь на среднее значение вращающего момента:
|
∂M 12 |
1 |
T |
|
M ср = |
∂α |
|
i1i2 dt |
( 4.6) |
|
||||
|
T ∫0 |
|
||
При установившемся отклонении справедливо соотношение M = МПР =Wα и:
|
1 |
∂M 12 |
1 |
T |
|
α = |
|
|
|
i1i2 dt |
(4.7) |
W |
|
|
|||
|
∂α |
T ∫0 |
|
||
Если токи i1 и i2 синусоидальны и имеют фазовый сдвиг ψ, то
1 T
T ∫0 i1 i2 dt = I1 I2cosψ ,
где I1 и I2 -среднеквадратические (действующие) значения токов. Следовательно
α = |
1 |
∂M12 |
I1 I2 cosψ |
(4.8) |
|
W |
|||||
|
∂α |
|
|
отсюда следует, что показания прибора определяются произведением токовi1 иi2 и
углом ψ. При ψ = 90o отклонение равно нулю.
При последовательном соединении катушек |
i1 = i2 и |
|||
α = |
1 |
∂M12 |
I 2 |
(4.9) |
|
||||
|
W ∂α |
|
|
|
Если прибор используется для измерения напряжения, то последовательно с подвижной катушкой включают дополнительный резистор Rдоб, который ограничивает ток через прибор. Показания прибора определяются формулой
α = |
1 |
∂M 12 |
U 2 |
(4.10). |
|
W ∂α |
|||||
|
|
|
|||
Для сокращения, обычно прибор электродинамической системы в схемах
132
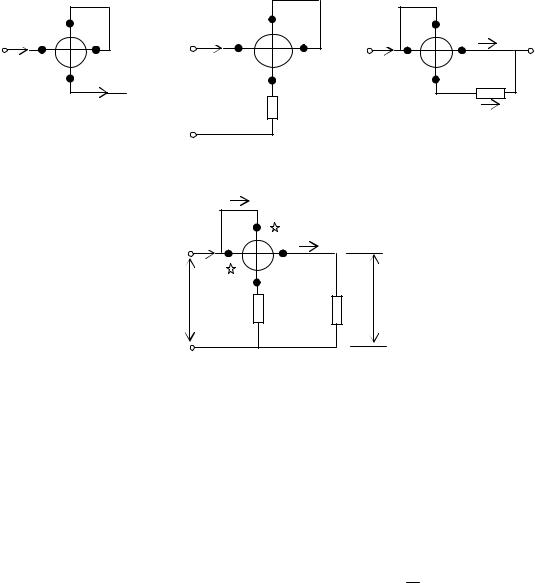
133
подключения изображается условно, как это показано на рис. 4.22. а,б,в,г.
Здесь рис.4.22.а – схема включения при измерении тока. Неподвижная катушка представляется горизонтальной линией с двумя точками подключения, соответственно подвижная катушка – вертикальной. При измерении тока катушки включаются последовательно и величина отклонения определяется формулой (4.9) . Как видно из этой формулы величина отклонения пропорционально квадрату тока протекающему по катушкам. Из этого следует во-первых, что шкала прибора нелинейна и, во-вторых, полярность включения прибора не имеет значения, поскольку при возведении в квадрат минус превращается в плюс.
i |
|
i |
i1 |
|
U |
|
|
i |
|
Rдоб |
i2 |
а) |
|
б) |
в) |
|
|
|
|
|
i2 |
|
|
|
i |
i1 |
|
U |
Rдоб |
RН |
UН |
|
г)
Рис. 4.22.
Параллельное включение обмоток используется в амперметрах, рассчитанных на большой ток (рис. 4.23.в). При этом основную часть тока пропускают по неподвижной катушке, которая наматывается толстым проводом. При этом уменьшается ток i2 через рамку.
Введя коэффициент распределения токов по обмоткам k = i1 i2
И обозначив измеряемый ток i = i1 +i2 , из (4.9.) имеем
133
134
α = |
1 k |
∂M12 |
I 2 |
(4.11). |
|||
|
|
|
|||||
W (k +1)2 |
|||||||
|
∂α |
|
|
||||
Подбирая величину k можно построить прибор для измерения больших токов. Независимое включение катушек электродинамического механизма применяется в ваттметрах приборах для измерения мощности. Схема включения катушек показана на рис. 4.22, г. Неподвижная катушка с малым сопротивлением включается последовательно с нагрузкой RН. Подвижная катушка с последовательно включенным резистором Rдоб подключается параллельно нагрузке. При таком соединении отклонение подвижной части прибора пропорционально средней активной мощности рассеиваемой на нагрузке за период Т, т. е.
1 |
|
∂M12 |
|
1 T |
1 |
|
∂M12 |
|
|
||
α = |
|
|
|
|
|
∫uнiн dt = |
|
|
|
Pн |
(4.12.). |
WR |
|
∂α |
|
T |
WR |
|
∂α |
||||
|
доб |
|
|
|
|
0 |
доб |
|
|
|
|
При измерении мощности в цепях переменного тока иногда требуется измерять реактивную мощность PQ =UI sinφ . Приборы, измеряющие PQ называют варметрами.
В этих приборах создается искусственный фазовый сдвиг 90° между напряжением, приложенным к параллельной цепи, и током в рамке. В этом случае
|
1 ∂M 12 |
|
π |
|
1 |
|
∂M 12 |
|
|
|||
α = |
|
|
|
UI cos ϕ + |
|
|
= − |
|
|
|
UI sinϕ |
(4.13). |
W |
|
∂α |
2 |
W |
|
∂α |
||||||
|
|
|
|
|
|
|
|
|||||
Знак минус в 4.13. указывает, что стрелка отклоняется в обратную сторону. Для нормальной работы прибора необходимо переключить концы обмоток. Зажимы, обозначенные звездочкой (*) на рис. 4.22, г, называются генераторными и подключаются со стороны генератора.
Основная погрешность электродинамических приборов на постоянном токе определяется механическими свойствами устройства, постоянством параметров измерительной цепи и точностью градуировочной характеристики. Механические свойства могут быть доведены до высокой степени совершенства. Стабильность параметров измерительной цепи повышается, если в качестве дополнительного сопротивления используется проволочный резистор (из манганина). Градуировку
134
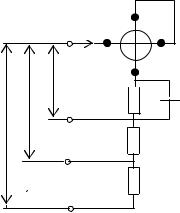
135
можно выполнить весьма точно на постоянном токе с помощью образцовых приборов (компенсаторов), Однако постоянный ток лучше измеряется магнитоэлктрическими приборами (так как электродинамические потребляют мощность 3...15 Вт). Поэтому
представляет интерес градуировка |
на |
постоянном токе с последующим |
использованием прибора на переменном токе. |
|
|
В вольтметрах (рис. 4.22.б) частотная погрешность вызывается индуктивным сопротивлением его цепи. Поэтому если прибор градуирован на постоянном токе, при измерении переменных токов возникнет существенная погрешность.
Достаточно эффективной частотной коррекцией является последовательное включение резисторов R1 ,R2 ,R3 и шунтирование одного из них конденсатором как показано на рис.4.4.4.
i
U3 |
U2 U1 |
R1 
 C
C
R2
R3
Рис.4.23..
Вольтметр, градуированный на постоянном токе, но с частотной коррекцией, можно применять на частотах до 2….3 кГц при классе точности 0,2. При использовании электродинамического прибора в качестве амперметра катушки включаются последовательно (рис. 4.22.а), в этом случае изменение активного сопротивления (например, от температуры) и изменение индуктивного сопротивления (при изменении частоты) не вызывает погрешности измерения, поскольку прибор показывает тот ток который через него протекает. Если амперметр рассчитан на больше ток и его обмотки включаются параллельно (рис. 4.22в), то погрешность измерения определяется перераспределением токов между ветвями при изменении температуры и частоты. Для коррекции в схему вводят резисторы R1 и R2 и
135
136
конденсатор C1 (рис. 4.25.).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис.4.24. |
|
|
|
|||||||||||||
При выполнении условия |
L1 R1 |
= L2 R2 удается устранить перераспределение токов |
|||||||||||||||||||||||
при изменении частоты. |
Шунтирование R2 конденсатором C1 устраняет |
различие |
|||||||||||||||||||||||
показаний на постоянном и переменном токах. |
|
|
|
||||||||||||||||||||||
По |
сравнению |
с |
|
приборами |
магнитоэлектрической |
системы |
|||||||||||||||||||
электродинамические приборы более чувствительны к внешним полям. Экранирование прибора экраном из ферромагнитного материала существенно ослабляет влияние внешних полей. Другой прием носит название астазирование. В приборах с асмтазированием используются две подвижные тушки, которые создают два вращающих момента. Катушки расположены так, что внешнее магнитное поле увеличивает один вращающий момент и настолько же уменьшает другой. Сумма моментов остаётся неизменной. Астатические механизмы электродинамической системы применяются сравнительно редко, так как имеют сравнительно сложную конструкцию.
4.5.Электромагнитные приборы.
Кэлектромагнитным относятся такие приборы, в которых поле, созданное неподвижной катушкой с протекающим по ней током, воздействует на один или несколько сердечников из ферромагнитного материала, эксцентрично расположенных на оси. Подвижная часть стремится расположиться так, чтобы энергия системы катушки была наибольшей. Измерительный механизм (рис. 4.24.) состоит из катушки
136
137
F с обмоткой из медного провода, имеющей воздушный зазор, и сердечника 3 Сердечник укреплен на оси 1. Противодействующий момент создается спиральной пружиной 4, которая в
|
Рис.4.24. |
отличие от |
ранее рассмотренных приборов магнитоэлектрической и |
электродинамической систем не используется для подведения тока, так как катушка F неподвижна. Стрелка 2 снабжена противовесами для механической балансировки механизма. Корректор 5 служит для корректировки установки стрелки, обеспечивая совмещение ее с нулевой отметкой шкалы при отсутствии сигнала.
Вращающий момент определяется соотношением (4.3). Энергия магнитного
поля системы зависит от квадрата тока к индуктивности катушкиL W |
M |
= |
1 |
i2 L |
. При |
|
2 |
||||||
|
|
|
|
повороте подвижной части сердечник выполненный из магнитного материала, перемещается относительно катушки, что вызывает изменение индуктивности. Следовательно, мгновенное значение вращающего момента в соответствии с уравнением Лагранжа (4.4):
|
|
|
|
M = |
1 |
|
∂L |
|
i2 |
(4.14). |
||||
|
|
|
|
|
∂α |
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
Среднее значение вращающего момента: |
|
|||||||||||||
|
|
ср = |
1 |
T∫M dt = |
1 |
∂L |
|
1 |
T∫i2 dt . |
|
||||
M |
|
|||||||||||||
|
|
|
|
|
||||||||||
|
|
|
T 0 |
|
|
2 ∂α T 0 |
|
|||||||
137

138
Так как |
1 |
T∫i2 dt − квадрат действующего значения тока, то |
|||||||
|
|||||||||
|
T o |
|
1 |
|
∂L |
|
|||
|
|
|
|
ср |
= |
I 2 |
(4.15). |
||
|
|
M |
|||||||
|
|
|
2 |
∂α |
|||||
|
|
|
|
|
|
|
|
||
Величина отклонения указателя так же как и в ранее рассмотренных приборах, определяется из условий равновесия M = Wα . Подставив в данную формулу значение среднего момента (4.15) имеем:
α = |
1 ∂L |
I 2 |
(4.16) |
|||
|
|
|
||||
2W ∂α |
||||||
|
|
|
||||
Как видно из (4.16), отклонение подвижной части зависит от квадрата действующего значения тока. Однако вид шкалы зависит так же от закона изменения
dLdα , т. е. от формы и расположения сердечника. Обычно подбором формы сердечника
удаётся добиться равномерности шкалы на некоторых ее участках. При измерении тока электромагнитным прибором его катушка включается последовательно в измерительную цепь. Для изменения пределов измерения катушка делается секционированной. Для измерения токов до 100.. .200 А приборы снабжается катушкой из одного витка толстой медной шины. Температурная погрешность амперметров электромагнитной системы невелика и определяется изменением упругих свойств пружины. Частотная погрешность возникает из-за вихревых токов в сердечнике и поверхностного эффекта в проводах катушки. При использовании многожильного провода можно использовать прибор на частотах до 2….3 кГц. При измерении постоянного тока показания прибора различаются при возрастающих и убывающих изменениях тока. Это связано не только с трением оси подвижной части в опорах крепления но и явлением гистерезиса сердечника. При использовании электротехнической стали погрешность из-за гистерезиса может составить 5%, изготовление сердечника из пермаллоя позволяет снизить эту погрешность до 0,2%. В вольтметрах электромагнитной системы включается дополнительный резистор Rдоб, выполненный из манганина. Компенсация температурной зависимости эффективна, если сопротивление добавочного резистора существенно превышает сопротивление катушки.
Вольтметры электромагнитной системы выпускают классов 1,0; 1,5; 2,5 с
138
139
верхними пределами измерения 0,5...600 В. Электромагнитные приборы нашли широкое применение благодаря простоте конструкции, низкой стоимости, высокой надежности. Поскольку ток проходит только по неподвижной катушке, которая может быть намотана толстым проводом, приборы рассматриваемого типа способны выдерживать большие перегрузки. Зависимость закона отклонения от формы
сердечника ∂∂Lα (формула 4.16) позволяет влиять на характер шкалы, создавать
перегрузочные амперметры с растянутой шкалой при малых значениях измеряемой величины и сжатой шкалой при больших ее значениях.
На рис.4.25 и 4.26 показаны разновидности конструкций приборов магнитоэлектрической системы.
Рис. 4.25
На рис. 4.25 показан электромагнитный измерительный механизм с круглой неподвижной катушкой А, внутри которой укреплен стальной сердечник С Ю.
С наружной стороны катушка закрыта стальным экраном, уменьшающим влияние внешних магнитных полей.
Подвижная часть имеет ось и укрепленные на ней сердечник С1 Ю1 , указательную стрелку, спиральную пружину, алюминиевый сектор Г магнитоиндукционного успокоителя и противовес П, уравновешивающий подвижную часть. При прохождении измеряемого тока по катушке сердечники намагничиваются одноименно и отталкиваются друг от друга образуя вращающий момент.
На рис. 4.26 показана полная конструкция прибора электромагнитной системы.
139
140
Здесь применена плоская неподвижная катушка 1 и плоский сердечник 2, укрепленный на оси 3, вращающийся в опорах 4, стрелка 5 перемещается относительно шкалы 6. На шкале укреплен ограничитель 7, ограничивающий ход стрелки. Противовесы 8, спиральная пружина 9, корректор 10 и 11 выполняют описанные ранее функции.
Рис. 4.21
Рис. 4.26.
Вприборе применен успокоитель воздушного типа, состоящий из подвижной 12
инеподвижной частей 13.
4.6.Электростатические приборы.
Вэлектростатических приборах перемещение подвижной части механизма осуществляется под действием энергии электрического поля системы заряженных проводников. Поэтому электростатические приборы обычно используются в качестве вольтметров. Наибольшее распространение получил механизм, конструкция которого показаны на рис. 4.6.1. Эта конструкция применяется в щитовых и переносных вольтметрах, измеряющих напряжения до нескольких сотен вольт.
Вприборе рис. 4.6.1 секторообразные пластины 1 образуют подвижную часть прибора. Она поворачивается на оси вместе со стрелкой. Силы электрического поля стремятся повернуть подвижную часть относительно неподвижной 1 так, чтобы энергия электрического поля была максимальна. Поскольку энергия
140
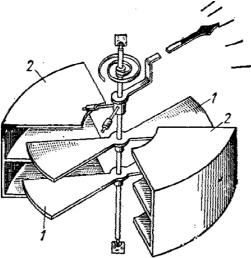
141
Рис.4.27.
(W = CU 2 /2) будет максимальна при максимальном значении емкости, под воздейст-
вием приложенного напряжения U подвижный электрод будет втягиваться между неподвижными. Смена полярности приложенного напряжения не изменяет направления отклонения. Поэтому электростатические приборы можно применять на переменном токе. При этом из-за инерции подвижная часть не может следовать за изменениями вращающего момента и реагирует на его среднее значение
Вращающий момент электростатического механизма
M = |
∂Wэл = |
1 |
U 2 |
∂C |
. (4.17) |
|
2 |
∂α |
|||||
|
∂α |
|
|
Величина отклонения, соответствующая условию равновесия M = −Mпр = Wα ,
определяется соотношением:
α = |
1 |
|
∂C |
U 2 |
(4.18), |
2W |
|
∂α |
|||
|
|
|
|
из которого видно, что отклонение пропорционально квадрату приложенного
141
142
напряжения. Смена полярности приложенного напряжения не изменяет направления отклонения. Поэтому электростатические приборы можно применять на переменном токе. При этом из-за инерции подвижная часть не может следовать за изменениями вращающего момента и реагирует на его среднее значение:
M ср = |
1 |
∂C |
1 |
T u 2 |
∂C |
= |
1 |
U 2 |
∂C |
(4.19), |
|
|
∂α |
2 |
∂α |
||||||
|
2 ∂α T ∫0 |
|
|
|
||||||
где U — действующее значение переменного напряжения.
Вращающий момент электростатического механизма мал, поэтому вольтметры данного тина рассчитаны на предел более 10 В. Собственное электростатическое поле прибора мало, поэтому необходима экранировка от внешних полей. На показания электростатического прибора практически не влияет температура, частота, форма напряжения, а также внешние магнитные поля. Собственное потребление энергии вольтметром чрезвычайно мало и на постоянном токе равно нулю.
Для расширения пределов измерения электростатического вольтметра при измерении постоянных напряжений целесообразно применять резистивный делитель, а при измерении переменных - емкостный. Схемы делителей показаны на рис. 4.28. а, б.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
U |
|
|
R1 |
|
|
|
|
PV1 |
PV1 |
|
|
PV1 |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|||
|
|
|
|
а) |
|
|
|
Рис.4.28. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При использовании емкостного делителя измеряемое напряжение U и напряжение на |
||||||||||||||||||||||||
вольтметре UV |
определяются соотношением: |
|
U |
= |
(C1 + C2 + CV ) |
, где CV - |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UV |
|
C2 |
||||||||
электрическая емкость вольтметра.
Промышленность выпускает электростатические вольтметры классов точности 0,5; 1,0; 1,5 на напряжения от 10 В до 300 кВ. Частотный диапазон до 10 МГц. Основное применение электростатические вольтметры находят для измерений в
142
143
маломощных цепях при широком частотном диапазоне, а также в цепях высокого напряжения.
4.6. Термоэлектрические приборы.
Действие термоэлектрических приборов основано на преобразовании измеряемого переменного тока в постоянный ток и измерении последнего с помощью магнитоэлектрического прибора. В основу термоэлектрического прибора положено использование термопреобразователя, состоящего из нагревателя и термопары. В качестве нагревателя используется, тонкая проволока, изготовленная из термостойкого материала, например из нихрома и константана. Измеряемый ток, проходя по нагревателю выделяет тепловую энергию, которая повышает температуру спая термопары, состоящей из двух разнородных проводников (например, железа и константана).
Различают контактные термоэлектрические преобразователи, у которых спай
|
мкА |
мкА |
|
мкА |
|
|
|
|
|
||
|
Iт |
1 |
Iт |
|
Iт |
|
M |
N |
|||
|
M 1 N 2 |
M |
N |
|
|
|
i |
A |
Б |
||
i |
|
|
|||
с |
3 |
2 |
|
|
|
|
в) |
|
|||
|
|
|
|
|
|
|
а) |
б) |
Рис.4.29 |
|
|
|
|
|
|
|
термопары непосредственно приварен к середине нагревателя (рис. 4.29 а), и бесконтактные термоэлектрические преобразователи (рис. 4.30 б), у которых спай термопары 1 и нагреватель 2 разделены изолятором. В качестве изолятора используется стеклянная бусина. Через нее передается теплота от нагревателя к термопаре. Термо – э.д.с. зависит от материала проводников термопары и возрастает с увеличением разности температур горячего и холодного концов.
Термоэлектрические свойства металлов принято оценивать значением термо – э.д.с. термопары с проводниками из данного металла и платины. Термо – э.д.с. считается положительной, если ток во внешней цепи термопары протекает от
143
144
данного металла к платине, и отрицательной - при обратном направлении тока. Например, при температуре 4000С термопара железо-платина дает термо – э.д.с. 5,5 мВ, а термопара константан – платина – термо - э.д.с. -15,3 мВ. Термо – э.д.с. термопар не содержащих платины, определяется как алгебраическая разность термо- э.д.с. двух термопар, каждая из которых содержит один из металлов исследуемой термопары и платину. Например, при tГ= 4000С термо - э.д.с. термопары железоконстантан составит: 5,5 – (-15,3)=20,8 мВ, причем ток во внешней цепи будет протекать от железа к константану. Если температура холодных концов tх отличается от нуля, то результирующая термо - э.д.с. определяется как разность термо - э.д.с. при температурах tГ и tх . Например для той же термопары железо-константан при tГ = 4000С и tх = 500С результирующая термо - э.д.с. составит Е=20,8-2,5=18,3 мВ.
Чтобы получить большую термо-э.д.с. проводники термопары изготавливают из металлов, значительно различающихся по их термоэлектрическим свойствам и допускающий длительный нагрев до 600-10000С.
Существенное значение имеет теплопроводность проводников термопары и окружающей ее среды, поскольку замедленный отвод тепла от термопары приводит к тепловой инерции прибора. Для хорошего отвода тепла от холодных концов термопары и стабилизации их температуры эти концы присоединяют к массивным медным или латунным зажимам.
С целью улучшения отвода тепла от горячего спая проводники термопары делают тонкими, диаметром не более 0,1 мм. Длина проводников обычно не превышает 1 см, а их сопротивление составляет единицы или несколько десятков Ом.
Спай (точка с на рис. 4.7.1 а) является тепловыделяющим концом термопары. К теплопоглощающим (холодным) концам подключается магнитоэлектрический измерительный механизм, показания которого пропорциональны термо - ЭДС. Изоляционная прослойка между нагревателем и термопарой увеличивает инерционность и уменьшает чувствительность. Однако изоляция обеспечивает большую точность измерений, поскольку измеряемый ток, протекающий по нагревателю, не ответвляется в цепь термопары.
В контактном термоэлектрическом преобразователе часть измеряемого тока протекает через термопару и прибор за счет падения напряжения на месте сварки. Это явление свойственно также термопреобразователю типа «термокрест» (рис.4.24в), в
144
145
котором нагреватель и термопара изготавливаются из одних и тех же проволочек, расположенных крестообразно и свариваемых в точке пересечения. Приборы с термокрестом используюся для измерения малых токов. Бесконтактные преобразователи позволяют последовательно соединять несколько термопар и получать «термобатарею» (рис.4.30). Термо - ЭДС возрастает пропорционально числу термопар, в результате чего повышается чувствительность прибора.
мкА



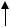 IТ
IТ
i

Рис.4.30.
Термо - ЭДС пропорциональна количеству теплоты, выделенной измеряемым током в месте спая. Количество теплоты, в свою очередь, пропорционально квадрату измеряемого тока.
Ток в цепи прибора |
I |
Т |
= |
E |
+ R |
, где R- сопротивление термопары, |
R |
|
- |
|
П |
||||||||
|
|
|
R |
П |
|
|
|
||
|
|
|
|
|
|
|
|
|
сопротивление прибора, Е – термо - ЭДС.
Как показывают расчеты и эксперименты, термо - ЭДС определяется соотношением
E = k′I 2 , где k′ - коэффициент пропорциональности; I- ток подогревателя.
Следовательно,
|
|
′ 2 |
|
||
IТ = |
k I |
(4.20) |
|||
(R + RП ) |
|
||||
Согласно отклонение стрелки магнитоэлектрического прибора |
|||||
α = |
|
SI k′ |
I 2 = kI 2 . |
(4.21) |
|
|
|
||||
|
|
R + RП |
|
||
Таким образом, если использовать термопреобразователь для измерения тока, шкала прибора оказывается квадратичной. Для нагрева спая термопары тратится лишь небольшая доля выделяющегося тепла. Большая часть его теряется в результате лучеиспускания, конвекции и теплопроводности элементов термопары. Для уменьшения потерь тепла термопара помещается в колбочку с высоким вакуумом. Вакуумные термопреобразователи обеспечивают при том же токе подогрева в 10...30 раз большую
145
146
термо-ЭДС и применяются в приборах с высокой чувствительностью.
На термопреобразователях строятся вольтметры и амперметры. Широко применяются термоэлектрические приборы для измерения напряжения и тока типа Т131...Т133. Прибор Т131 позволяет измерять напряжения 75.. 1500 мВ на частотах 20 Гц...1 МГц при токе потребления 0,1 мА. Прибор Т133 измеряет ток 100...1000 мкА в диапазоне частот 20 Гц... 0,5 МГц. Термоэлектрические преобразователи пригодны для измерения мощности, причем шкала термоваттметра линейна.
На погрешности термоэлектрических приборов влияют главным образом три фактора: изменение температуры окружающей среды, длительность включения и изменение частоты измеряемого тока. Погрешность из изменения температуры окружающей среды обусловлена изменением сопротивления цепи измерительного механизма и сопротивления нагревателя. Термо - ЭДС термопары от температуры внешней среды практически не зависит, так как нагреваются одновременно как теплопоглощающие, так и тепловыделяющие концы термопары. Влияние длительности включения проявляется в том, что показания прибора оказываются различными и в зависимости от того, как долго был включен прибор, так как нагреватель, имеющий меньшую массу, прогревается гораздо быстрее, чем массивные токоподводящие колодки, которые тоже несколько нагреваются. Поэтому разность температур между тепловыделяющим спаем и теплопоглощающими концами термопары, удаленными от колодок, оказывается непостоянной и зависящей от продолжительности включения.
Влияние частоты на показания термоэлектрических приборов сказывается по двум причинам. С ростом частоты вследствие поверхностного эффекта растет сопротивление нагревателя, а также проявляются паразитные параметры схемы. Оба фактора проявляются на частотах свыше 3-..5 МГц. Рациональным конструированием приборов удается обеспечить изменение токов до 100 МГц при классе точности 1,0 и 1,5,
К недостаткам приборов термоэлектрической системы следует отнести малую перегрузочную способность (допускаются перегрузки не более 50%), сравнительно большое потребление энергии.
146
147
Глава 5. Измерительные цифровые приборы.
5.1. Основные принципы построения цифровых измерительных приборов.
Цифровой измерительный прибор (ЦИП) — средство измерений, автоматически вырабатывающее сигналы измерительной информации в цифровой форме. Цифровой измерительный прибор имеет ряд преимуществ перед аналоговыми приборами: удобство отсчитывания значений измеряемой величины, возможность полной автоматизации процесса измерений, регистрация результатов измерения с помощью цифропечатающих устройств. Поскольку результат измерения в ЦИП выражен в цифровом коде, измерительную информацию можно вводить в ЭВМ. Не следует, однако, считать, что ЦИП в будущем полностью вытесняет аналоговые приборы. Аналоговые приборы просты и надежны. В тех случаях, когда оператору необходимо следить за уровнями изменяющихся во времени сигналов, стрелочные указатели более удобны из-за наглядности представления об изменениях величины, о ее минимальном значении, приближении к порогу и т. п.
В ЦИП происходит преобразование непрерывной измеряемой величины в цифровой код. Осуществляется этот процесс с помощью аналого-цифрового преобразователя (АЦП), в котором сигнал измерительной информации подвергается дискретизации, квантованию и кодированию [52].
Дискретизация, т. е. процесс преобразования непрерывного сигнала измерительной информации в дискретный, может осуществляться как по времени, так и по уровню. Дискретизация по времени выполняется путем взятия отсчетов сигнала Х(t) в определенные детерминированные моменты времени. Таким образом, от сигнала измерительной информации сохраняется только совокупность отдельных значений. Промежуток времени t между двумя моментами дискретизации называют шагом дискретизации. Обычно моменты отсчетов на оси времени выбираются равномерно, т. е. шаг дискретизации t постоянен.
Дискретизация значений измерительного сигнала по уровню ноcит название квантования. Операция квантования сводится к тому, что непрерывная по времени и амплитуде величина заменяется ближайшим фиксированным значением по установленной шкале дискретных уровней. Эти дискретные (разрешенные) уровни образованы по определенному закону с помощью мер. Разность Х между двумя разрешенными уровнями называют интервалом (шагом или ступенью) квантования. Интервал квантования может быть как постоянным, так и переменным. Временная дискретизация измерительного сигнала имеет смысл, когда его величина изменяется во времени. Если
148
измерительный сигнал постоянен, достаточно осуществить квантование. Особым случаем является измерение времени (временного интервала). Процесс дискретизации здесь теряет смысл, и осуществляется квантование самого времени.
Следующим преобразованием измерительного сигнала, является кодирование. Цифровым кодом называется последовательность цифр или сигналов, подчиняющаяся определенному закону, с помощью которой, осуществляется условное представление численного значения величины. Графически описанные преобразования поясняются на рис. 5.1. Исходный измерительный сигнал Х (t) (рис. 5.1, а) представляет собой непрерывную функцию времени. Дискретизация выполняется с интервалом t. Моменты дискретизации отмечены на рис.5.1,а цифрами 1, 2, 3 ..., 9. Практически такую дискретизацию можно осуществить путем амплитудной модуляции исходным сигналом Х (t} последовательности коротких импульсов с периодом t. Как видно из рис. 5.1в, значения сигнала X (ti )
полученные после дискретизации, точно соответствуют мгновенным значениям функции Х (t). Если на том же рисунке отметить уровни квантования, расположенные друг от друга на расстоянии Х, то часть дискретных значений сигнала окажется в промежутках между ними. Процесс квантования по уровню сводится к округлению дискретных значений сигнала до значений, соответствующих ближайшим разрешенным уровням. Так, в момент
1 мгновенное значение сигнала превышает уровень X 3 на величину, несколько меньшую
X /2 (см. рис. 5.1,6). Округление производится в сторону уменьшения и квантованное значение выбирается равным Х3. В момент 2 значение сигнала превышает уровень Х4 на величину, большую чем X /2. Квантованное значение принимается равным X5, (рис. 5.1,
в). Послед этап заключается в преобразовании квантованного сигнала X(ti )кв |
в |
цифровой код. На рис. 5.1, г представлен для примера цифровой |
|
149
x(t)
а)
t
1 2 3 4 5 6 7 8 9
x(ti)кв
x11
x7
б) x5 x3
x1 |
t |
|
1 2 3 4 5 6 7 8 9
x(ti)кв
в)
t
1 |
2 |
3 |
|
4 |
|
|
|
5 |
6 |
|
7 |
|
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x(ti)кв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодовая группа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
n2 |
|
n3 |
|
|
|
|
n4 |
|
|
|
n5 |
|
|
n6 |
|
|
|
n7 n8 n9 |
||||||||||||||||||||||||||||||||||||||||||
Рис.5.1
унитарный код X (ti )код , соответствующий значениям квантованного сигнала. При таком способе кодирования число импульсов в кодовой группе прямо пропорционально уровню квантованного сигнала. Например, отсчету 7 соответствует уровень квантования X6 , и в кодовой группе n7 содержится шесть импульсов.
Из рис. 5.1 ясно, что при дискретизации и квантовании сигнала возникает погрешность преобразования. Непрерывная функция Х (t) анализируется только в
150
моменты дискретизации. На интервале t между двумя отсчетными точками сигнал предполагается неизменным. Уменьшением интервала t , т.е. сближением отсчетных точек можно добиться снижения погрешности до допустимой величины. При измерении постоянных величин погрешность преобразования, связанная с дискретизацией, равна нулю. Погрешность, возникающая при квантовании непрерывной измеряемой величины, обусловлена конечным числом уровней квантования. Эта погрешность характерна для всех ЦИП, она носит название погрешности дискретности д. При равномерном квантовании погрешность д находится в пределах0 ≤ д ≤ X . Следующий этап преобразований в ЦИП заключается в превращении цифрового кода в показания цифрового отсчетного устройства. Для этого необходим дешифратор, который превращает кодовые группы в соответствующие напряжения, управляющие работой цифрового индикатора.
Рассмотренная последовательность преобразований, осуществляемая в аналогоцифровом преобразователе (АЦП), дешифраторе и цифровом индикаторе, конечно дает упрощенное представление о работе ЦИП. Примером может служить случай измерения постоянной величины. Для этого достаточно одного цикла преобразований, в результате которого получится кодовая группа. Но кодовая группа это «пакет» импульсов, передаваемый в течение короткого интервала времени. Результат измерений должен сохраняться на экране достаточно долго, например до следующего цикла. Поэтому в состав ЦИП должно входить запоминающее устройство (ЗУ). Более детальное описание структурной схемы будет дано после изучения отдельных элементов ЦИП. В заключение параграфа перечислим возможные режимы работы ЦИП и их характеристики.
Режим однократного измерения. Этот режим удобен, когда измеряемый параметр сигнала постоянен. Команда на проведение измерения подается оператором, результат измерения хранится в запоминающем устройстве и воспроизводится на цифровом индикаторе. В ЦИП осуществляется квантование измерительного сигнала и его кодирование.
Режим периодического измерения. Процесс измерения повторяется периодически через интервал t , установленный оператором. В ЦИП осуществляются операции дискретизации, квантования и кодирования. После каждого цикла измерения результат на экране цифрового индикатора обновляется.
Следящий режим измерения. Цикл измерения повторяется, после того как изменение измеряемой величины превысит ступень квантования.
151
Помимо погрешности измерения, к числу важных характеристик ЦИП относится его быстродействие, время измерения и помехоустойчивость. Под быстродействием ЦИП понимается максимальное число измерений, выполняемых в единицу времени с нормированной погрешностью. Время измерения - интервал от начала цикла преобразования измеряемой величины до получения результата. Под помехоустойчивостью понимают способность ЦИП с нормированной погрешностью производить измерения при наличии помех.
Быстродействие ЦИП достаточно высокое. Современная элементная база позволяет строить ЦИП, обеспечивающие до 107 преобразований в секунду. Такое быстродействие требует запоминания результатов измерений, поскольку регистрирующие устройства не обеспечивают фиксацию результатов измерений с указанной скоростью. При визуальном наблюдении требования к быстродействию резко снижаются, поскольку оператор способен оценить не более 2—3 результатов измерений в секунду.
5.2. Функция преобразования цифрового измерительного прибора.
Под функцией преобразования измерительного прибора понимается зависимость его показаний от значения измеряемой величины. Различают номинальную и реальную функции преобразования. У приборов, шкала которых проградуирована в значениях измеряемой величины, X=Y , т.е. показание равно измеряемой величине и характеристика преобразования представляет собой прямую линию расположенную под углом 450 по отношению к горизонтальной оси. В цифровых приборах из-за квантования сигнала характеристика преобразования является ступенчатой функцией (рис. 5.2), определяемой выражением
Y = qInt[X / q + 0,5sign X ]. |
(5.1) |
В 5.1. Int[A] – функция «целая часть А», sign A – функция «знак числа А»: sign A=1
при А≥0 и sign A=-1 , при А<0.
Функция преобразования, наилучшим образом приближающаяся к линейной У = Х изображена на рис. 5.2.

152
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
Y=Х |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Ymax |
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xmin |
|
|
|
|
|
|
|
|
|
|
|
Xi |
|
|
Xmax |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ymin |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта функция, соответствующую формуле 5.1, называют функцией преобразования идеального квантователя. При q→0 в пределе функция 5.1 совпадает с линейной У = Х. Поскольку величина q имеет конечное значение и реальный квантователь вносит погрешность в результат измерения. Эта погрешность обусловлена самим методом аналого-цифрового преобразования, при котором бесконечному множеству возможных значений измеряемой величины ставится в соответствие конечное значение счетное множество возможных показаний. Таким образом, погрешность квантования может быть
отнесена |
к методическим погрешностям. По определению абсолютная, |
погрешность |
любого |
СИ равна разности = Y-X. Математическое выражение |
методической |
погрешности идеального квантователя может быть получено с помощью выражения 5.1.
k = Y − X = qInt[X / q + 0,5sign X ]− X . |
(5.2) |
Графически зависимость погрешности от измеряемой величины представлена на графике рис. 5.3.
k
+0,5q
X/q
-1 |
1 |
q
-0,5q
Рис 5.3
На рис. 5.3. по горизонтальной оси откладывается относительная величинаотношение измеряемой величины к ступени квантования. Как видно из рис. 5.3, погрешность идеального квантователя является периодической функцией измеряемой величины.
153
Период этой функции равен ступени квантования q, а ее экстремумы ±0,5 q. Поскольку функция погрешности известна, и она не изменяется при повторном измерении, её можно считать систематической. Однако такое утверждение не может быть признано корректным, так как по определению систематическая погрешность может быть исключена путем введения поправок. В данном случае это не представляется возможным. Принято считать, что погрешность квантователя является неслучайной функцией случайной величины. Однако измеряемая величина X, может принимать случайные значения в пределах от Xmax до Xmin . Поэтому по ансамблю измеряемых величин погрешность квантования может рассматриваться как случайная величина. По ансамблю результатов измерений неизменного значения X погрешность k остается постоянной, но неизвестной.
Как видно из рис. 5.3 максимальное значение погрешности, связанной с квантованием измеряемой величины составляет ±0,5 q. Чем меньше q, тем меньше погрешность. Закономерен вопрос о рациональном выборе величины q. Утверждение чем меньше, тем лучше, не может быть взято за основу выбора, поскольку уменьшение q без увеличения числа уровней квантования Nq приведет к сокращению диапазона измеряемой величины. Например, если число уровней квантования Nq , десять, а ступень квантования q равна 1В, то очевидно, что максимальное значение измеряемого напряжения равно
Umax = Nq· q=10В. Если же предположить, что q = 0,1В, то Umax =1В. Таким образом уменьшение ступени квантования(кванта) а десять раз привело к уменьшению максимального значения измеряемой величины так же в десять раз. Можно компенсировать уменьшение Umax соответствующим десятикратным увеличением числа уровней квантования. Однако увеличение числа уровней квантования усложняет аппаратурную реализацию цифрового прибора.
К решению вопроса о рациональном выборе ступени квантования и их числа, можно подойти на основе требований к Nmax – максимальному числу, которое должно индицироваться цифровым прибором. Каждая ячейка цифрового табло может отображать цифры от нуля до девяти. Если цифровое табло рассчитано на отображение трех разрядов десятичного числа, то максимальное число, которое может быть отображено Nmax =999, если табло имеет четыре разряда, то Nmax =9999 и т.д. Эти цифры обычно являются конечными значениями диапазона измерения шкалы цифровых приборов. Отметим, что такие цифры никогда не выбираются для оцифровки шкал аналоговых приборов. Дело в том, расширение диапазона измерения, которое получается, если вместо 999 выбрать цифру 1000, равно единице младшего разряда, составляющую всего 1/1000 от выбранного диапазона. Для такого «расширения» в цифровом приборе необходимо предусмотреть еще
154
один цифровой индикатор и все элементы, которые им управляют (счетные устройства, дешифратор и т.п.). В аналоговом приборе все изменения заключаются в нанесении одной дополнительной отметке на шкале, т.е. никак не влияют на его стоимость.
При нормировании погрешности цифровых средств измерений используется параметр, носящий название: цена единицы наименьшего (младшего) разряда кода. В (???????) он обозначался μ. При применении квантования показание цифрового прибора Y=qX. Ступень квантования q определяет не только погрешность цифрового прибора, но и его чувствительность, под которой понимается соотношение S = 1/q. При изменении измеряемой величины показание прибора изменяется лишь при условии, если её положительное или отрицательное приращение превысит q, поэтому, чем меньше q, тем выше чувствительность. Конечное значение шкалы цифрового прибора определяет не только диапазон измерений, но и его разрешающую способность. Под разрешающей способностью понимают величину обратную конечному значению шкалы, т.е. Nmax . Так если Nmax= 999, разрешающая способность составляет 1:999. Следует отметить, что такое определение разрешающей способности справедливо в случае когда q=μ , а следовательно, изменение измеряемой величины на одну ступень квантования q, вызывает соответствующее изменение выходного кода на минимальную ступень μ. Можно построить цифровой прибор, в котором выполняется соотношение q=kμ, где k=1,2…- любое цело число. В этом случае ступень квантования q расширяется в целое число раз. Так, например, если k=2, а μ –цена единицы младшего разряда выходного кода соответствует 1В, то из-за расширения ступени квантования q в два раза, изменения показания прибора будут происходить лишь тогда, когда измеряемая величина изменится на величину, кратную 2В. Иными словами цифры нечетные 1,3, 5 и 9 в младшем разряде цифрового отсчета индицироваться не будут. Будут индицироваться только четные цифры и ноль. Аналогично можно показать, что при k=5, будут индицироваться цифры 0 и 5.
Количество ступеней квантования, которое необходимо обеспечить при проектировании прибора определяется числом, выражающим конечное значение шкалы. При полном использовании старшего разряда (когда в нем отображается цифра 9), Nmax= рn-1, где р- основание системы счисления, n- число разрядов. В десятичной системе р=10. Если принять n=4, k=1 необходимое ступеней квантования составит величину
Nq = рn-1=104-1=10000-1=999. Такой результат вполне понятен, так при k=1 устройство квантования должно изменять выходной код при приращении входного сигнала на пороговую величину q. Если пороговая величина 1В, то для отсчета 999 В необходимо предусмотреть 999 ступеней квантования.
155
Помимо погрешностей, возникающих в цифровых приборах, связанной с процедурой квантования необходимо учитывать инструментальные погрешности, возникающие от
Y
 Номинальна
Номинальна
 q
q
q |
Реальная |
Yi
инс
X
Рис. 5.4
Отклонения реальной характеристики преобразования от номинальной. На рис. 5.4. показаны возможные отклонения, которые возникают, как вследствие нарушение шага квантования по осям Х и Y, так и смещению характеристики относительно осей в целом. Величина инструментальной погрешности инс при одном значении измеряемой величины, показана на рис. 5.4. как расстояние между сплошной линией, соединяющей центры площадок номинальной функции преобразования и пунктирной линией построенной аналогичным образом для реальной функции.
Y,B |
|
|
|
5,999 |
|
|
|
|
H |
|
|
5,997 |
|
|
|
5,995 |
|
|
|
5,996 |
5,998 |
6,000 |
X,B |
|
Рис. 5.5. |
|
|

156
Другим видом искажений функции преобразования, является гистерезис, заключающийся в том, что значение выходного значения измеряемой величины, зависит от направления, в котором изменялась измеряемая величина при подходе к этому значению. На рис. 5.5. приведен экспериментально снятый участок характеристики преобразования цифрового вольтметра Щ1412 [52]. Стрелками показано направление изменения напряжения, подаваемого на вход прибора при снятии соответствующей ветви реальной функции преобразования. Штриховой линией показана функция преобразования идеального квантователя. На рис.5.5 так же обнаруживается еще одно аномальное явление для цифровых приборов - пропуск кодов. Наибольшее отклонение между возрастающими и убывающими участками, связанное с явлением гистерезиса, обозначено Н.
Гистерезис функции преобразования вызывается особенностями технических характеристик схемных элементов, входящих в состав конструкции приборов. Это прежде всего наличие элементов, обладающих гистерезисом, наличие гистерезиса характеристик срабатывания или зоны нечувствительности сравнивающих устройств и т.п. При увеличении скорости работы прибора могут проявляться недостаточно высокие динамические свойства сравнивающего устройства, когда время затухания переходных процессов превышает период частоты опроса разрядов.
При работе прибора все рассмотренные ранее погрешности влияют на результат измерения одновременно. Абсолютное значение суммарной случайной погрешности цифрового измерительного прибора может быть определено из соотношения
= o ИНС + о Н + |
МЕТ . |
(5.3) |
|
Первые два слагаемых, входящих в 5.3. являются независимыми случайными |
|||
величинами, так как они вызваны независимыми случайными процессами. Слагаемое |
мет |
||
– является неслучайной функцией |
измеряемой |
величины, поэтому дисперсия мет |
не |
может в общем случае суммироваться с дисперсиями первых двух слагаемых. Однако, если рассматривать измеряемую величину как случайную по ансамблю значений, то составляющая мет может рассматриваться как независимая случайная величина. В этом случае среднее квадратическое отклонение случайной погрешности измерений может быть рассчитано по формуле
σ = σ 2 + H 2 / 12 + q2 /12 , |
(5.4) |
где σ – среднее квадратическое отклонение случайной погрешности цифрового измерительного прибора.
157
5.3. Коды, применяемые в цифровых средствах измерений
Дискретизированные и квантованные значения функции в ЦИП кодируются. На рис. 5.1, г показан унитарный код, при котором число передаваемых импульсов пропорционально квантованному значению измеряемой величины. Представление числового значения в унитарном коде имеет недостатки. Число импульсов в кодовых группах различно, чем больше представляемое число, тем больше импульсов содержит кодовая группа. Так, для представления числа 82 необходимо передать 82 импульса. Привычная для нас десятичная система счисления более экономна. Действительно, в ней для построения чисел используется десять цифр: 0, 1, 2, 3, ..., 9. Число представляется в виде последовательности цифр. Каждая цифра занимает в нем определенную позицию (разряд). Например, число 482 содержит три цифры. Однако крайняя правая цифра 2 относится к разряду единиц, цифра 8 к разряду десятков, 4 - к разряду сотен. Таким образом, для представления данного числа в десятичной системе количество необходимых разрядов равно числу записанных цифр, т. е. трем. Запись этого же числа с помощью унитарного кода потребовала бы 482 импульса (знака). Экономность десятичной системы объясняется тем, то перемещение цифры влево на соседнюю позицию увеличивает ее значение в 10 раз. Цифра 10 является основанием десятичной системы счисления. Принципиально можно образовать систему счисления, используя с любое число р в качестве ее основания.
Десятичная система позволяет легко выразить дробную часть величины. Для этого достаточно отделить целую часть запятой и цифры, записанные правее запятой, будут представлять десятые, сотые и т.д. доли. Прежде чем перейти к рассмотрению других систем счисления, рассмотрим позиционный принцип представления чисел с помощью ряда. В качестве примера используем число 482, 317:
482,317 = 4•102+8•101 + 2•10°+3•10-1 + 1•10-2 +7•10-3.
Каждое слагаемое относится к определенному разряду, например 4·102 — к разряду сотен. Здесь 102 весовой коэффициент, а 4— разрядный коэффициент. В общем случае число в произвольной системе счисления с основанием р представляется рядом:
N = an pn + an−1 pn−1 + ..... + a1 p0 + a−1 p−1 + a−2 p−2 + .....a−m p−m , (5.1),
где. pn ,p−n ,....p−m -весовые коэффициенты соответствующих разрядов, а an ,an−1.....,a−m -
разрядные коэффициенты. .
Используя (5.1), можно на позиционном принципе строить различные системы
158
счисления. Наибольший интерес для измерительной техники представляет двоичная система с основанием р = 2. Основное ее достоинство заключается в том, что для представления цифр разряда используется лишь два символа: 0 и 1. Например, число 11011,01 записано в двоичной системе счисления. Соответствующее ему число в привычной десятичной системе определяется с помощью (5.1):
11011, 01==l•24+l•23+0•22+l•2l+l•20+0·2-l+l•2-2 == 27,25.
Весовые коэффициенты разрядов, расположенных слева от запятой, равны соответственно
2° == 1; 21 = 2; 22 = 4; 23 = 8, т. е. 1, 2, ; 4, 8, 16 и т. д. Таким образом, весовой коэффициент старшего разряда превышает весовой коэффициент предыдущего (младшего) разряда в 2 раза (а не в 10 раз, как в десятичной системе). Удобство применения двоичной системы счисления в цифровой технике связано с простотой построения запоминающих устройств (ЗУ). Хранить n-разрядные числа можно с помощью устройств, содержащих n элементов, каждый из которых запоминает соответствующую цифру числа. Для запоминания цифры каждого разряда двоичного числа могут использоваться устройства с двумя устойчивыми состояниями (триггеры). Одному из состояний триггера ставится в соответствие цифра 1, другому – 0.
Однако число, записанное в двоичной системе счисления, неудобно для визуального определения. Перевод его в десятичное число требует довольно сложных схем, поскольку нет непосредственной разбивки на десятичные разряды. По этой причине в ЦИП пользуются так называемым двоично-десятичным кодом. Двоичнодесятичный код образуется путем представления каждой цифры десятичного числа соответствующим двоичным числом. Например, число 27 в десятичной системе преобразуется следующим образом. Цифра 2 записывается как 0010, а цифра 7 как 0111, т. е. 2710 =0010 01112/10. Здесь индекс 10 свидетельствует о записи в десятичной системе, а 2/10 — в двоично-десятичной.
Отметим, что представление десятичного числа в двоично-десятичной системе с точки зрения числа символов менее экономно, чем в двоичной системе. Например, для числа 27 в двоично-десятичной системе надо иметь 8 символов, а в двоичной только 5 (11011). Но простота реализации ЦИП, работающих в двоично-десятичной системе представления, компенсирует этот недостаток.
В двоично-десятичном коде для представления каждой десятичной цифры используются четыре символа. Меньшим количеством обойтись нельзя, так как с помощью трех символов можно образовать лишь 8 комбинаций, а количество возможных цифр в каждом разряде десятичного числа равно 10 (0...9). Вместе с тем четыре символа (тетрада) позволяют построить 16 комбинаций, т. е. 6 комбинаций оказываются
159
лишними. На первый взгляд вполне естественным кажется исключение тех комбинаций, которые выражают десятичные цифры более 9. Например, число 1011 равно 10, оно превышает возможный разрядный коэффициент в десятичной системе и может быть удалено. Код 1, содержащий 10 начальных комбинаций (табл. 5.1), соответствующих выражению цифр от 0 до 9 в двоичной системе счисления, называют кодом «8421». Однако он не является единственно возможным. Для каждой из десяти цифр вполне допустимо совершенно произвольное закрепление кодовых комбинаций. Поэтому число принципиально возможных тетрадно-десятичных кодов довольно велико. Код I I в табл. 5.1 аналогичен коду I в пределах от 0 до 8, а число 9 закодировано с пропуском шести кодовых комбинаций. Это привело к невозможности выражения кода весами отдельных разрядов. Этот код называется символическим, в отличие от кода I, который является позиционным. Код III также позиционный. Он имеет разрыв между числами 7 и 8, что меняет вес первого разряда. Его называют кодом «2421»
Таблица 5.1.
Десятичные |
|
|
Коды |
|
|
числа |
|
|
|
|
|
1 («8421») |
II |
|
III(«2421») |
IV(«2421») |
|
|
|
|
|
|
|
|
|
Веса двоичных |
разрядов |
|
|
|
|
|
|
|
|
0 |
0000 |
0000 |
|
0000 |
0000 |
|
|
|
|
|
|
1 |
0001 |
0001 |
|
0001 |
0001 |
|
|
|
|
|
|
2 |
0010 |
0010 |
|
0010 |
0010 |
|
|
|
|
|
|
3 |
0011 |
0011 |
|
0011 |
0011 |
|
|
|
|
|
|
4 |
0100 |
0100 |
|
0100 |
0100 |
|
|
|
|
|
|
5 |
0101 |
0101 |
|
0101 |
1011 |
|
|
|
|
|
|
6 |
0110 |
0110 |
|
0110 |
1100 |
|
|
|
|
|
|
7 |
0111 |
0111 |
|
0111 |
1101 |
|
|
|
|
|
|
8 |
1000 |
1000 |
|
1110 |
1110 |
|
|
|
|
|
|
9 |
1001 |
1111 |
|
1111 |
1111 |
|
|
|
|
|
|
Код IV (код Айкена) имеет разрыв между цифрами 4 и 5. В этом месте проходит ось симметрии. Каждая кодовая комбинация над осью отличается от симметричной комбинации под осью инверсными значениями разрядных коэффициентов. Так, десятичное число 3 воспроизводится кодовой комбинацией 0011. Симметрично расположенное относительно оси число 6 – комбинацией 1100. Эта комбинация может быть получена из 0011, если нули заменить единицами, а единицы нулями. Это свойство,
160
называемое самодополнением, полезно при реализации арифметических операций с двоичными числами и, в частности, вычитания.
5.4. Аналого-цифровое преобразование и отображение информации в цифровых приборах.
Аналого-цифровой преобразователь (АЦП) – узел цифрового измерительного прибора, в котором последовательно осуществляется преобразование непрерывной измеряемой величины в дискретные отсчеты (дискретизация), квантование выбранных отсчетов и кодирование, - представление измеряемой величины в цифровом коде, т.е. в последовательности нулей и единиц. Известно множество АЦП. Однако методы, используемые при их построении, можно разбить на три основные группы.
1. Время-импульсный метод, заключающийся в предварительном линейном преобразовании значения измеряемой величины во временной интервал с последующим непосредственным кодированием временного интервала.
2.Частотно-импульсный метод, основанный на преобразовании значения измеряемой величины в пропорциональное значение частоты с последующим преобразованием в код.
3.Метод следящего уравновешивания (взвешивания), состоящий в поочередном сравнении измеряемой величины с суммой образцовых дискретных величин, изменяющихся по определенному закону.
Времяимпульсный метод преобразования.
Преобразовать значение измеряемой величины во временной интервал можно с помощью вспомогательного пилообразного напряжения. На рис. 5.6а показана постоянная измеряемая величина UX и вспомогательное линейно нарастающее напряжение и Uл =βt В момент t1 значениё пилообразного напряжения оказывается равным нулю, что служит командой для формирователя стробирующих. импульсов, который начинает вырабатывать импульс прямоугольной формы (рис. 5.6 б). В момент t2 линейно нарастающее напряжение достигает значения UX. В этот момент вырабатывается команда на окончание импульса, и напряжение на выходе генератора Uстр уменьшается до нуля. Сигналы команд вырабатываются в сравнивающем устройстве (нуль-органе), которое имеет два входа (Uх и Uл ). Когда Uх= Uл на выходе сравнивающего устройства появляется импульс.
161
|
u |
|
|
|
Ux |
|
Uл |
|
|
|
|
а) |
|
|
Ux |
|
|
β |
t |
|
|
|
|
|
t1 |
|
t2 |
|
|
2 |
|
|
Ucтр |
|
|
б) |
|
|
t |
|
|
Тх |
|
|
Ucч |
|
|
в) |
|
|
|
|
|
|
t |
|
Uкод |
N |
|
г) |
|
Tсч |
|
|
|
Тх |
t |
|
|
|
|
|
|
|
Рис.5.6 |
|
|
|
В |
момент t1 значениё пилообразного напряжения оказывается равным нулю, что служит командой для формирователя стробирующих. импульсов, который начинает вырабатывать импульс прямоугольной формы (рис. 5.6 б). В момент t2 линейно нарастающее напряжение достигает значения UX . В этот момент вырабатывается команда на окончание импульса, и напряжение на выходе генератора Uстр уменьшается до нуля. Сигналы команд вырабатываются в сравнивающем устройстве (нуль-органе), которое имеет два входа (Uх и Uл ). Когда Uх= Uл на выходе сравнивающего устройства появляется импульс.
Таким образом измеряемая величина Uх преобразуется во временной интервал TX. При этом сохраняется линейная зависимость между TX и Uх . Нетрудно убедиться из рис. 5.6,а, что если изменить значение Uх, например, в сторону уменьшения, становится меньше и длительность импульса.
Следующий этап преобразования заключается в преобразовании временного интервала в код. Для этого служат счетные импульсы Uсч (рис.5.6,в), следующие с периодом Тсч . Этими импульсами заполняется временной интервал TX. Выполнить эту операцию можно с помощью стробирующего устройства, пропускающего счетные импульсы на свой выход, когда на один из его входов поступает разрешающий сигнал.
162
В качестве разрешающего (стробирующего) сигнала используется прямоугольный импульс длительностью TX . На выходе стробирующего устройства получаем группу
(пакет) из N счетных импульсов. Число импульсов в пакете может быть определено их соотношения длительности стробирующего импульса TX и периода Тсч : N= TX/ Тсч.
Таким образом число импульсов в пакете при фиксированном периоде счетных импульсов пропорционально TX, которое в свою очередь пропорционально измеряемому напряжению Uх (см. рис.5.6,а.).
Сигнал Uкод, представленный на рис.5.6,г, является унитарным кодом измеряемой величины. Напомним, что с унитарным кодом читатель уже встречался при рассмотрении вопросов дискретизации и кодировании. На рис. 5.1г показаны кодовые группы состоящие из пакетов, количество импульсов в которых определяется величиной сигнала в отсчетный момент. В данном случае измеряемая величина Uх является постоянной и для ее определения достаточно одного пакета.
Поскольку унитарный код не экономичен (например, для представления числа 100 в привычной для нас десятичной системе счисления нужно три символа, а в унитарном коде необходимо сто импульсов), необходимо преобразовать унитарный код в другой код, например двоично-десятичный. Такое преобразование может быть осуществлено путем подсчета количества импульсов в пакете- N. Действительно, как следует из рис.5.6а, Uх = TX tg β. Значение tg β = Uх / TX = V есть скорость нарастания напряжения, В/с.
Следовательно, Uх = TX V. Так как TX = N Тсч , имеем
Uх = Тсч V N. ( 5.5)
Из( 5.5) видно что при постоянных величинах Тсч и V число счетных импульсов N
пропорционально измеряемой величине Uх и, следовательно, сигнал показанный на рис. 5.2,г, является ее унитарным кодом. Преобразование унитарного кода может быть осуществлено простым подсчетом импульсов. Поскольку импульсные счетные устройства обычно выполняются на триггерных ячейках, имеющих два устойчивых состояния равновесия, счет производится в двоичной системе счисления (одному устойчивому состоянию придается значение «0», а другому «1»). Поскольку визуальный отсчет результата измерения в двоичной системе затруднителен, осуществляется преобразование двоичного кода в привычный для нас десятичный код. Однако результат измерения в двоичном коде представляет интерес не только как промежуточное преобразование в случае если информация обрабатывается далее в цифровом виде. Например, в цифровом виде сигнал может подаваться на компьютер или другие цифровые измерительные приборы.
163
Структурная схема АЦП с время-импульсным преобразованием представлена на рис. 5.7. Генератор счетных импульсов в данном устройстве является мерой. К нему, как и к любой мере предъявляются высокие требования в отношении точности. В данном случае речь идет о точности и стабильности частоты, поскольку период Тсч есть величина обратная частоте. На один из входов сравнивающего устройства подается измеряемый сигнал Uх, на другой Uл – сигнал от генератора пилообразного напряжения. Сравнивающее устройство выдает кратковременные импульсы в те моменты времени, когда пилообразное напряжение равно нулю (момент t1 на рис. 5.7,а) и когда равно Uх (момент t2) . В состав сравнивающего устройства входят два нуль-органа, один из которых фиксирует момент t1, а другой t2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Генератор счетных |
|
|
|
|
|
Стробирующая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Счетчик |
|
|
|
|
|
|
||||
|
импульсов ТСЧ |
|
|
|
|
|
схема |
|
|
|
|
|
|
|
|
Выход |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формирователь |
|
|
|
|
|
Устройство |
|
|
|
|
|
||
|
|
|
|
|
|
|
стробимпульсов |
|
|
|
|
|
управления |
|
|
|
|
|
||
|
UX |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Генератор |
|
|
|
|
|||||
|
|
|
|
Сравнивающее |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
пилообразного |
|
|
|
|
||||
|
|
|
|
|
|
|
устройство |
|
|
|
|
|
|
|
|
|
|
|||
|
Вход |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
напряжения UЛ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.7
Импульсы со сравнивающего устройства поступают формирователь стробирующих импульсов, который из двух кратковременных импульсов формируют прямоугольный импульс длительностью TX , управляющий работой стробирующей схемы. Через открытую стробирующую схему в течение времени TX импульсы поступают на счетчик, который фиксирует результат счета в двоичном коде. Устройство управления формирует сигналы для управления счетчиком и генератором пилообразного напряжения.
Начало процесса измерения может инициироваться двумя способами. Первый способ, когда измерение представляет собой однократный процесс. В этом случае начало измерения создается устройством управления после нажатия кнопки на панели прибора. Во втором случае устройство управления периодически выдает управляющие импульсы, запускающие генератор пилообразного напряжения. При этом результат измерения периодически обновляется.
Помимо задания начала цикла измерения, управляющее устройство подает импульсы на счетчик, устанавливая ноль в счетчике. Это необходимо, как в начале работы
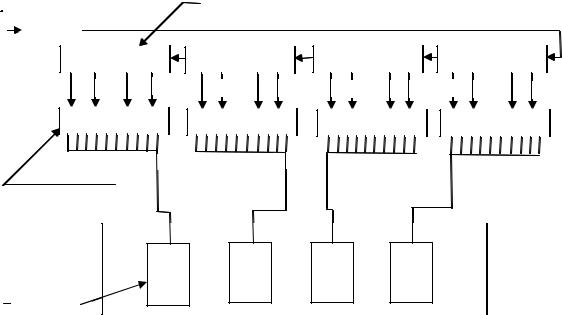
164
устройства (так как при включении питания триггеры счетчика устанавливаются в произвольное состояние), так и при повторении цикла измерения, поскольку измеряемое напряжение может изменяться во времени и для обновления результата в счетчике должен быть установлен ноль.
Дальнейшие преобразования в цифровом измерительном приборе поясняются на рис.5.8, где показана структурная схема преобразования унитарного кода последовательно в двоично-десятичный код и двоично-десятичного кода в привычное десятичное представление результата измерения.
Счетные импульсы поступают на вход и далее последовательно на четыре счетные декады. Счетная декада устроена таким образом, что каждый импульс, поступающий на ее вход, фиксируется в ее памяти. Роль памяти выполняет триггерная ячейка. Так как один триггер может иметь только два устойчивых состояния равновесия, он может запомнить либо «0» либо «1». Если включить два триггера последовательно, то такая пара в состоянии запомнить 4 цифры (конечно в двоичном коде), если включить три
Счетнаядекада
Вход
|
IV |
|
|
|
|
III |
|
|
|
|
IIII |
|
|
|
I |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
IV |
|
|
|
|
III |
|
|
|
|
II |
|
|
|
I |
|
0 |
|
9 |
|
0 |
|
|
9 |
0 |
|
|
|
9 |
0 |
|
|
9 |
Дешифратор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цифровой |
|
|
2 |
|
0 |
|
|
8 |
|
4 |
|
|
|
|
||
индикатор |
|
|
|
|
|
|
|
|
|
|
||||||
Отсчетноеустройство
Рис. .5.5. 8.
триггера, то 8 цифр, а если четыре, то 16. В последнем случае только после 16 импульсов в всех ячейках снова установятся нули и счет начнется снова. Естественно, что рассуждения справедливы только в случае когда во всех ячейках к началу счета были
165
установлены нули.
Для того, что бы построить счетную декаду, т.е. устройство которое считало бы до десяти необходимо произвести изменения в схеме. Обычно они сводятся к организации обратных связей между триггерами. В книгах по импульсной технике подробно описывается как это можно сделать. Отметим только, что введение обратных связей позволяет лишь уменьшить количество фиксируемых результатов, поэтому для организации счетной декады необходимо иметь минимум четыре триггера.
При последовательном включении декад происходит следующее. Декада I реагирует на каждый импульс поступающий на вход, т.е. считает от нуля до десяти. Каждый десятый импульс поступает на счетную декаду II, которая считает каждый десятый импульс поступающий на вход. Аналогично счетная декада III считает каждый сотый импульс, декада IVкаждый тысячный. Таким образом каждая декада фиксирует один разряд десятичного числа. Внутри декады каждое десятичное число представлено в двоичном коде. Таким образом произошло преобразование унитарного кода в двоично - десятичный код.
Дальнейшее преобразование осуществляется с помощью четырех дешифраторов. На каждый из дешифраторов информация поступает от соответствующих счетных декад. Поскольку в каждой декаде имеется четыре триггера, для съема информации с них достаточно иметь четыре линии. Электрические потенциалы на линиях (высокие или низкие) соответствуют зафиксированным в декадах числах. Таким образом каждый дешифратор имеет четыре управляющих входа. Количество выходов у дешифратора зависит от вида применяемого индикатора. На рис. 5.8. у дешифраторов имеется десять выходов. Обычно такие дешифраторы используются с индикаторами, в которых в стеклянном баллоне, наполненным инертным газом, расположены в виде пакета (но изолированно друг от друга) цифры, изготовленные из тонкой проволоки. При подаче управляющего напряжения между проволочными цифрами, играющими роль катода и расположенной сзади сеткой (анодом) образуется тлеющий разряд. Форма тлеющего разряда соответствует форме катода. Газоразрядные индикаторы требуют для управления достаточно больших напряжений, что является недостатком.
Альтернативным вариантом построения цифровых индикаторов является применение светоизлучающих диодов (светодиодов) и жидких кристаллов. Достоинством светодиодов следует отнести низкие рабочие напряжения, что позволяет осуществить их управление с помощью микросхем, высокая яркость, малая потребляемая мощность и долговечность. Светодиодные индикаторы выполняются из дискретных элементовсегментов. Получили распространение семи и девятисегментные конструкции,
166
показанные на
Рис. 5.9.
рис.5.9. Для создания конкретной светящейся цифры необходимо на соответствующие сегменты подать возбуждающие светодиод напряжения. Для управления семи сегментным индикатором нужно иметь дешифратор с восьмью управляющими выводами и одним общим, соответственно для управления девятью сегментным индикатором необходимо десять выводов.
Как видно из рис. 5.8, для индикации результата измерений, состоящего из четырехзначного десятичного числа необходимо иметь четыре счетные декады, четыре дешифратора и четыре индикатора. Набольшее число, которое может быть отображено на индикаторе9999. Для получения привычного для аналоговых приборов конечного значения в виде «круглого» числа, например 10000, т.е. для увеличения предельного значения всего на единицу, необходимо усложнить прибор добавив один индикатор, один дешифратор и одну счетную декаду, что вряд ли целесообразно.
