
- •Московский технический университет
- •Проектирование цифрового фильтра
- •Свойства ких-фильтров
- •Задание требований к ачх
- •Структуры ких-фильтров
- •Процедура синтеза ких-фильтров методом окон
- •Синтез ких-фильтров методом окон в matlab
- •Код скрипта lr_05_low
- •Код скрипта lr_05_high
- •Код скрипта lr_05_high
- •Код скрипта lr_05_stop
- •Код скрипты внешних функций
Задание требований к ачх
Методы
синтеза частотно-избирательных
КИХ-фильтров изначально предполагают
ЛФЧХ, поэтому требования задаются к
нормированной АЧХ
 восновной полосечастот
восновной полосечастот и включают в себя:
и включают в себя:
частоту дискретизации
 ;
;граничные частоты полос пропускания (ПП) и полос задерживания (ИЗ), для которых введены условные обозначения:
-
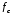 – граничная частота ПП для ФНЧ и ФВЧ;
– граничная частота ПП для ФНЧ и ФВЧ;
-
 – граничная частота ПЗ для ФНЧ и ФВЧ;
– граничная частота ПЗ для ФНЧ и ФВЧ;
-
 ,
, – левая и правая граничные частоты ПП
для ПФ и РФ;
– левая и правая граничные частоты ПП
для ПФ и РФ;
-
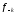 ,
, – левая и правая граничные частоты ПЗ
для ПФ и РФ;
– левая и правая граничные частоты ПЗ
для ПФ и РФ;
максимально допустимые отклонения АЧХ A(f), для которых введены условные обозначения:
-
 – от единицы в ПП (для ФНЧ, ФВЧ и ПФ);
– от единицы в ПП (для ФНЧ, ФВЧ и ПФ);
-
 – от нуля в ПЗ (для ФНЧ, ФВЧ и РФ);
– от нуля в ПЗ (для ФНЧ, ФВЧ и РФ);
-
 – от единицы в левой полосе пропускания
– ПП1 (для РФ);
– от единицы в левой полосе пропускания
– ПП1 (для РФ);
-
 – от единицы в правой полосе пропускания
– ПП2 (для РФ);
– от единицы в правой полосе пропускания
– ПП2 (для РФ);
-
 – от нуля в левой полосе задерживания
– П31 (для ПФ);
– от нуля в левой полосе задерживания
– П31 (для ПФ);
-
 – от нуля в правой полосе задерживания
– П32 (для ПФ).
– от нуля в правой полосе задерживания
– П32 (для ПФ).
На рисунке Рисунок 1–Рисунок 4 приведены примеры идеальной АЧХ и требований к АЧХ для фильтров различного типа избирательности.
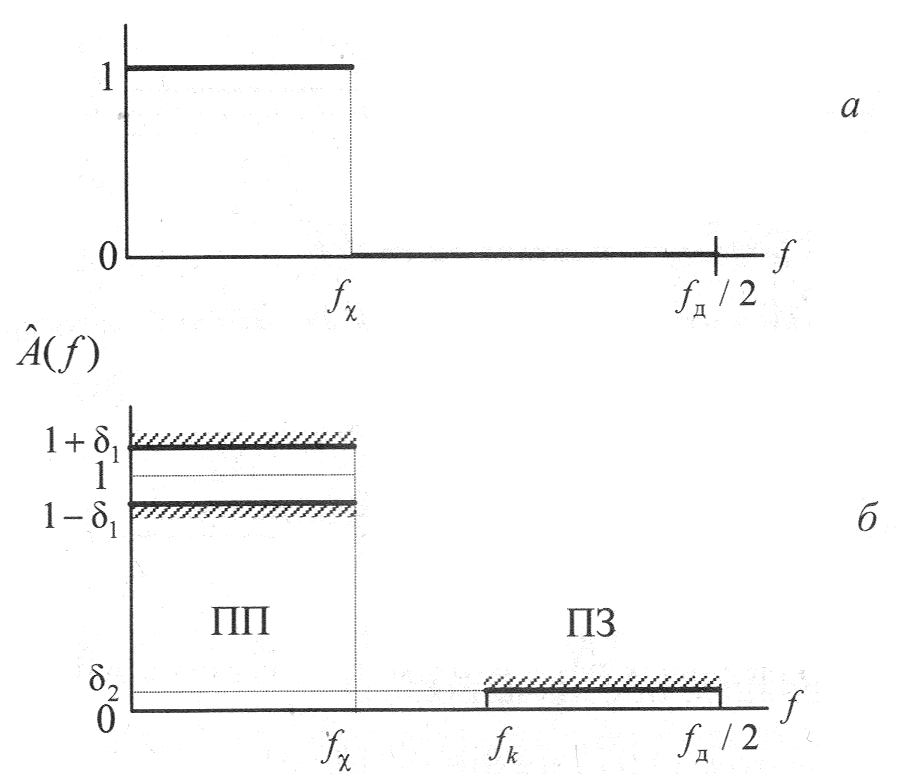
Рисунок 1. Идеальная АЧХ ФНЧ (а), требования к АЧХ ФНЧ (б)
Требования могут задаваться к АЧХ в децибелах – к характеристике ослабления:
 77\* MERGEFORMAT ()
77\* MERGEFORMAT ()
или к характеристике затухания:
 . 88\* MERGEFORMAT ()
. 88\* MERGEFORMAT ()
В MATLAB требования задаются к характеристике затухания – АЧХ (дБ).

Рисунок 2. Идеальная АЧХ ФВЧ (а), требования к АЧХ ФВЧ (б)

Рисунок 3. Идеальная АЧХ ПФ (а), требования к АЧХ ПФ (б)

Рисунок 4. Идеальная АЧХ РФ (а), требования к АЧХ (б) РФ (б)
В требованиях к характеристике затухания
8 вместо значений максимально допустимых
отклонений
 ,
, ,
, ,
, ,
, ,
, задаются:
задаются:
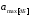 – максимально допустимое затухание
в ПП (для ФНЧ, ФВЧ и ПФ);
– максимально допустимое затухание
в ПП (для ФНЧ, ФВЧ и ПФ); – минимально допустимое затухание в
ПЗ (для ФНЧ, ФВЧ и РФ);
– минимально допустимое затухание в
ПЗ (для ФНЧ, ФВЧ и РФ);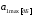 – максимально допустимое затухание
в ПП1 (для РФ);
– максимально допустимое затухание
в ПП1 (для РФ); – максимально допустимое затухание
в ПП2 (для РФ);
– максимально допустимое затухание
в ПП2 (для РФ); – минимально допустимое затухание в
П31 (для ПФ);
– минимально допустимое затухание в
П31 (для ПФ); – минимально допустимое затухание в
П32 (для ПФ).
– минимально допустимое затухание в
П32 (для ПФ).
На рисунке Рисунок 5 приведен пример требований к характеристике затухания ФНЧ.

Рисунок 5. Требования к характеристике затухания ФНЧ
Взаимосвязь
между значениями максимально допустимых
отклонений и их соответствующими
значениями в децибелах, например, между
 ,
и
,
и и
и и
и устанавливается формулами:
устанавливается формулами:
 ; 99\* MERGEFORMAT ()
; 99\* MERGEFORMAT ()
 , 1010\* MERGEFORMAT ()
, 1010\* MERGEFORMAT ()
и наоборот:
 ; 1111\* MERGEFORMAT ()
; 1111\* MERGEFORMAT ()
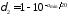 . 1212\* MERGEFORMAT ()
. 1212\* MERGEFORMAT ()
Структуры ких-фильтров
Структура(структурная схема) ЦФ отображаеталгоритмвычисления реакции по разностному уравнению и определяется видомпередаточной функции.
Структурные схемы КИХ-фильтров с ЛФЧХ приведены на рисунке Рисунок 6.
В MATLAB структура КИХ-фильтра с ЛФЧХ описывается в виде объекта dfilt:
Hd = dfilt. structure (b)
где Hd– имя объектаdfilt;dfilt– тип объекта;structure – функция, задающая конкретную структуру объектаHd(таблица 6);b– параметр функцииstructare– вектор коэффициентов передаточной функции 3.
Для КИХ-фильтров свойства объекта dfilt, выводимые по его имени, включают в себя:
Filterstructure – структура КИХ-фильтра;
Arithmetic – форма представления данных;
Numerator – коэффициенты передаточной функции;
PersistentMemory – начальные условия при вычислении реакции; значение false соответствует нулевым начальным условиям.

Рисунок 6. Структурные схемы КИХ-фильтров с ЛФЧХ: прямая приведенная с симметричной ИХ (Direct-Form Symmetric FIR) для КИХ-фильтра 1-го типа длины N=1 (а): прямая приведенная с антисимметричной ИХ (Direct-Form Antisymmetric FIR) для КИХ-фильтра 3-го типа длины N
Таблица 6. Функции structure и структуры КИХ-фильтров с ЛФЧХ
|
Функция structure |
Параметр функции structure |
Структура КИХ-фильтра |
|
dffir |
b – вектор коэффициентов передаточной функции 3 |
Direct-Form FIR (прямая) |
|
dfsymfir |
b– вектор коэффициентов передаточной функции 3, симметричных относительно N/2 |
Direct-Form Symmetric FIR (прямая приведенная с симметричной ИХ, см. рисунок Рисунок 6, а) |
|
dfasymfir |
b– вектор коэффициентов передаточной функции 3, антисимметричных относительно N/2; при четном N– b(N/2)=0 |
Direct-Form Antisymmetric FIR (прямая приведенная с антисимметричной ИХ, см. рисунок Рисунок 6, б) |
При синтезе КИХ-фильтров с ЛФЧХ методом окон ИХ может быть только симметричной, чему соответствует структура Direct-Form Symmetric FIR.
