Дискретное преобразование Фурье

Дискретным преобразованием Фурье(ДПФ) называется пара взаимно однозначных образований:

• прямое ДПФ (Discrete Fourier Transform — DFT):

88\* MERGEFORMAT ()

• обратное ДПФ (ОДПФ) (Inverse Discrete Fourier Transform — IDFT):

99\* MERGEFORMAT ()

где – дискретное нормированное время;– дискретная нормированная частота;– период дискретизации по частоте (разрешение по частоте),–-точечная последовательность, т. е. периодическая последовательность во временной области с периодом;–-точечное ДПФ, т. е. периодическая последовательность в частотной области с периодом,– период последовательности и ДПФ;– поворачивающий множитель;–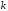-я дискретная гармоника.

Значения абсолютных частот дискретных гармоник связаны со значениями дискретных нормированных частот соотношением:

1010\* MERGEFORMAT ()

Дискретное преобразование Фурье 8 трактуется по-разному в зависимости от вида последовательности –периодическаяс периодомиликонечнаядлины N.

Для периодическойпоследовательностис периодомДПФ8 представляет собой ееспектрс точностью до множителя.

Модуль ДПФ (с точностью до множителя) называютамплитудным спектром, а аргумент– фазовым спектром периодической последовательности.

Амплитудный спектр вещественнойпериодической последовательности равен модулю ДПФс точностью до множителя:

1111\* MERGEFORMAT ()

При вычислении ДПФ 8 периодической последовательности она может задаваться на периоде или нацелом числе периодов, что не меняет результата.

Для конечнойпоследовательностидлиныДПФ8 представляет собойдискретных равноотстоящих значений ее спектральной плотностина периоде.

Для вещественныхпоследовательностей, периодических и конечных, модуль ДПФ–четная, а аргумент–нечетнаяфункция частоты.

Согласно определению, при вычислении ДПФ предполагается, что последовательность являетсяпериодической, и конечная последовательность представляет собойодин периодпериодической последовательности.

При этом точноевыделение гармоник последовательности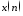с частотамигарантируется только в том случае, если они кратны периоду дискретизации частоте:

1212\* MERGEFORMAT ()

в свою очередь, возможно только в том случае, если на интервале последовательностиукладывается целое число периодов, т. е. отношение

1313\* MERGEFORMAT ()

является целым числом.

В случае, если условие 12 не выполняется, наблюдается эффект растекания спектра.

В MATLAB ДПФ 8 – 9 вычисляется с использованием алгоритмов БПФ²и ОБПФ с помощью функций:

X = fft(x)

x = ifft (X)

где Xиx–-точечные последовательностьи ее ДПФ– векторы, нижняя граница индексов которых равна единице, в отличие от ДПФ 8 – 9, где она равна нулю.

1. Выделение дискретных гармоник полезного сигнала

При вычислении ДПФ часто ставится задача автоматического определения значения модуля ДПФ , превосходящих некоторый заданный порог, и соответствующих дискретных нормированных частот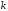. Фактически, эта задача сводится к выделению полезного сигнала в его аддитивной смеси с шумом.

В учебных целях мы ограничимся рассмотрением двух наиболее простых критериев, согласно которым значение модуля ДПФ 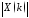аддитивной смеси сигнала с шумом относят к полезному сигналу:

• первый критерий – при заданном пороге значение модуля ДПФотносят к полезному сигналу, если выполняется условие:

1414\* MERGEFORMAT ()

• второй критерий – при заданном пороге значение модуля ДПФотносят к полезному сигналу, если выполняется условие:

1515\* MERGEFORMAT ()

где 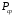– средняя мощность аддитивной смеси сигнала с шумом:

1616\* MERGEFORMAT ()

Значение порога , в первом критерии 14 задается в пределах:

1717\* MERGEFORMAT ()

а порога во втором критерии 15 – в пределах:

1818\* MERGEFORMAT ()

при условии, что

1919\* MERGEFORMAT ()

Граничные значения порогов в 17 и 18 можно определить только при априорно известных сигнале и шуме либо их моделях.

При обработке реальных сигналов значение порога , или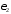задается исходя требований конкретной задачи.

2. Восстановление спектральной плотности

Спектральная плотность конечной последовательностидлины:

2020\* MERGEFORMAT ()

на периоде связана с отсчетами ДПФ8 соотношением:

2121\* MERGEFORMAT ()

Значения спектральной плотности 20 в равноотстоящих точках на периодеприопределяются по формуле:

2222\* MERGEFORMAT ()

где — дискретная нормированная частота, а— период дискретизации по частоте:

2323\* MERGEFORMAT ()

Тот же результат будет получен, если конечную последовательность длины дополнить нулями до длины:

2424\* MERGEFORMAT ()

и найти ее ДПФ 8, заменяя на:

2525\* MERGEFORMAT ()

С учетом 24 формула 25 принимает вид:

2626\* MERGEFORMAT ()

Следует помнить, что разрешение по частоте, под которым понимают минимальное расстояние между дискретными гармониками в ДПФ, определяется исключительно периодом дискретизации по частоте и при фиксированной частотезависит только от длины (периода) последовательности, поскольку именно она и только она определяет спектральный состав (дискретные гармоники) последовательности.

Поэтому увеличение длины конечной последовательности за счет добавления нулей и, соответственно, уменьшение периода дискретизации по частоте до, не меняет разрешения по частоте, а лишь улучшает условия различения близко расположенных частот дискретных гармоник.

3. Восстановление аналогового сигнала

Дискретное преобразование Фурье 8 может использоваться для восстановления аналогового периодического сигнала с финитным спектром, расположенным в области³, по формуле (усеченный ряд Фурье):

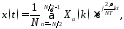2727\* MERGEFORMAT ()

где отсчеты связаны с отсчетами ДПФсоотношением:

2828\* MERGEFORMAT ()

Тот же результат будет получен при восстановлении аналогового сигнала непосредственно с помощью усеченного ряда Котельникова:

2929\* MERGEFORMAT ()

В MATLAB для этого удобно воспользоваться функцией:

sinc(t/T-n)

Приложение Б.