Анализ двоичной последовательности

Методы коррекции частотных характеристик тракта - методы позволяющие снизить межсимвольные помехи, происходящие от искажений I рода (из-за ограничения спектра сигнала сверху). Коррекция частотных искажений в области низких частот неэффективна, а потому для уменьшения межсимвольных помех из-за искажений II рода следует использовать такие сигналы в линии, у которых низкочастотные спектральные составляющие относительно невелики. Это достигается выбором определенного кода сигнала в линии. Вообще, сигналы в линии должны отвечать следующим условиям:

- спектр сигнала (область, где сосредоточено ~ 90% мощности) должен быть возможно сильнее ограничен, особенно в области нижних частот;

- структура сигнала должна позволять достаточно просто выделять из него сигнал тактовой частоты;

- должна обеспечиваться возможность контроля коэффициента ошибок в тракте без перерыва связи.

Рассмотрим вначале, в какой степени случайная последовательность в натуральном коде с вероятностью появления единиц ρ и коэффициентом скважности Кск=Тд/τи, представленная на рис. 4.15, удовлетворяет поставленным требованиям.

Рис. 4.15. Структура случайной двоичной последовательности

Как видно из рисунка, случайная последовательность импульсов с амплитудой U0в натуральном коде (верхняя осциллограмма) может быть представлена суммой регулярной (детерминированной) последовательности положительных импульсов с амплитудой pU0(средняя осциллограмма) и двух случайных последовательностей: положительных импульсов с амплитудой (1 - p)U0, и отрицательных - с амплитудой pU0.

Мощности этих последовательностей могут быть подсчитаны по следующим формулам.

Мощность исходной последовательности

Мощность детерминированной последовательности

тогда мощность случайных последовательностей составит

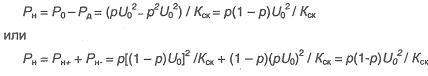
В зависимости от вероятности появления единиц р указанные мощности изменяются, как это показано на графике рис. 4.16.

Рис. 4.16. Зависимость мощности составляющих случайной последовательности от вероятности появления единиц

Амплитуды спектральных составляющих детерминированной последовательности представляют собой коэффициенты ряда Фурье

Соответственно дискретный энергетический спектр данной последовательности определяется выражением

В этом выражении синус квадратный множитель соответствует энергетическому спектру прямоугольного импульса и определяет частотную зависимость составляющих дискретного спектра а также огибающую непрерывного энергетического спектра случайной последовательности двоичных прямоугольных импульсов. Спектры для коэффициентов Кcк, равных соответственно 1, 2 и 4, а также для биимпульсов длительностью в один период тактовой частоты (о которых речь пойдет далее), показаны на рис. 4.17.

Рис. 4.17. Спектры прямоугольных импульсов: • мощность дискретных составляющих, u2/Гц

Обратимся к требованиям, сформулированным выше. Мы видим, что в случайной последовательности в натуральном коде поставленные требования практически не удовлетворяются. Во-первых, спектр сигнала относительно широк и в нем присутствует постоянная составляющая, что приводит к большим межсимвольным помехам. Во-вторых, хронирующий сигнал в спектре имеется, но при р → 0, его мощность также стремится к нулю, т.е. при передаче комбинаций, состоящих из больших пакетов нулей, выделение хронирующего сигнала будет затруднено. В-третьих возможность контроля появления ошибок отсутствует.

Для устранения основных недостатков первоначально был использован метод чередования полярности импульсов (код ЧПИ), т.е. символу «0» в этом коде соответствовала пауза, а символу «1» — последовательно импульсы положительной и отрицательной полярности. Действительно, как это следует из рис. 4.18, а, б, чередование полярности позволяет относительно хорошо компенсировать межсимвольные помехи I рода и, что особенно важно, — помехи II рода. Это обстоятельство позволяет предположить, что спектр сигнала в коде ЧПИ ограничен по сравнению с исходной последовательностью как сверху, так и снизу.

Рис. 4.18. Компенсация межсимвольных помех при применении кода ЧПИ: а - I рода; б - II рода

В сигнале с ЧПИ возможен контроль появления ошибок. Действительно, пропадание импульса или появление ложного приводит к нарушению чередования полярности, что легко контролировать по текущей сумме, которая не должна превышать единицы. Возможна даже коррекция ошибок методом Витерби (методом максимального правдоподобия — ошибка наиболее вероятна в бите, где амплитуда наиболее близка порогу принятия решения).

Дискретные составляющие в сигнале с ЧПИ также оказываются компенсированными, однако выделение хронирующего сигнала несложно — сигнал легко переводится в исходный путем двухполупериодного выпрямления. Однако если в исходной последовательности присутствуют большие пакеты нулей, выделение хронирующего сигнала существенно затрудняется. Преодоление этой трудности возможно несколькими способами.

Способ I. В исходной последовательности осуществляется инверсия четных (или нечетных) разрядов. При этом последовательности нулевых символов превращаются в последовательности вида «10101...». Способ применим в первичных системах, где появление в исходной последовательности комбинаций вида «10101...» (и, следовательно, превращение этих комбинаций в последовательности нулевых символов) маловероятно.

Способ II. Исходная последовательность скремблируется. Способ применим в любых системах, но понижает надежность ЦТС за счет возможной рассинхронизации скремблера и дескремблера.

Отметим, что код ЧПИ (AMI) был первым кодом для ЦТС, рекомендованным МСЭ-Т.