Расчет параметров системы цикловой синхронизации

Произведем расчет основных параметров системы цикловой синхронизации: среднего времени удержания синхронизмаи среднего времени восстановления синхронизмаВ основу расчета положим известное из математической статистики выражение для определения среднего временимежду пакетами из n событий, если вероятность события р, а период повторения опыта Т

 (2.4)

При определениив вышеприведенной формуле вероятностью события будет вероятность приема искаженной синхрогруппы рис, числом событий в пакете — число ячеек накопителя по выходу из синхронизма r1, а периодом повторения опыта — период посылки синхросигнала.

Вероятность приема искаженной синхрогруппы будет равна , где рош — вероятность появления ошибки в тракте, а b — число символов в синхрогруппе. В табл. 2.1 и 2.2 приведены результаты расчета , , что принято в системе передачи ИКМ-30).

Таблица 2.1

Результаты расчета

в зависимости от рош и r1 при b = 7 и Τ = 250 мс
r1	Рош
	10-3	10-4	10-5	10-6	10-7
1	36 мс	360 мс	3,6 с	36 с	~6 мин
2	5,2 с	8,5 мин	14ч	59 сут	16,2 г
3	12,3 мин	8,5 сут	23 г
4	29,5 ч	33,1 г
5	176 сут
6	69 лет

Таблица 2.2

Результаты расчета

в зависимости от b при рош =10-3, r1 = 4 и Τ = 250 мс
b	1	2	3	4	5
	~8 лет	180сут	36 сут	11,4сут	4,7 сут

Таким образом, как и ожидалось, среднее время удержания быстро снижается с ростом коэффициента ошибок в тракте передачи. Увеличением числа ячеек накопителя по выходу из синхронизма это снижение вполне можно компенсировать. Заметим, что увеличение числа символов синхросигнала довольно быстро снижает (это наблюдение понадобится при анализе среднего времени вхождения в синхронизм).

Определим среднее время восстановления синхронизма вх. Оно определяется следующими процессами. Во-первых, в течение r1. происходит заполнение накопителя по выходу из синхронизма (искаженная синхрогруппа приходит более чем r1раз), что является защитой от потери синхронизма при случайном искажении синхросигнала. Во-вторых, осуществляется скользящий поиск синхрогруппы и проверка ее на истинность в течение пцс. В-третьих, во избежание ложного входа в синхронизм, проверка на истинность повторяется r2 раз — происходит заполнение накопителя по входу в синхронизм r2. И, наконец, осуществляется вхождение в сверхцикловой синхронизм (если существует структура сверхциклов). Среднее время этого процесса равно среднему времени поиск сверхциклового синхросигнала сцс. Таким образом,

 (2.5)

Рассчитаем эти составляющие. Воспользовавшись формулой (2.4), определим r1, положив величину пакета событий равной емкости накопителя r1, вероятность события равной вероятности появления «1» на входе накопителя по выходу из синхронизма (точка с на рис. 2.12), и считая, что появление «1» и «0» в потоке равновероятно

.

Результаты расчета приведены в табл. 2.3.

Таблица 2.3

Результаты расчета

Зависимость r1 (мс) от b иr1приТ= 250 мс
	b
r1	1	2	3	5	7
1	0,5	0,333	0,286	0,258	0,252
2	1,5	0,778	0,612	0,525	0,505
3	3,5	1,37	0,985	0,799	0,762
4	7,5	2,16	1,41	1,08	1,02

Среднее время заполнения накопителя по выходу из синхронизма растет пропорционально увеличению числа ячеек в нем. С ростом числа символов в синхрогруппеубывает, но относительно медленно (снижениепроисходит гораздо быстрее).

Воспользовавшись формулой (2.4), несложно показать, что r2 ≈ r2(в системе ИКМ-30 r2 = 1). Действительно, здесь вероятность события — прием истинной синхрогруппы (появление единицы в точке d (рис. 2.12):

Поэтому

.

Среднее время восстановления сверхциклового синхронизма сцс равно полусумме наименьшего и наибольшего времен поиска сверхциклового синхросигнала. Для системы передачи ИКМ-30, например, наименьшее время соответствует случаю, когда сверхцикловой сигнал находится в данном (нулевом) цикле. Поскольку он расположен в середине цикла, а длительность цикла равна 125 мкс, наименьшее время будет 125/2 ~ 62,5 мкс. Наибольшее время будет, если сверхцикловой сигнал находится в последнем (15-м) цикле, и составит

Таким образом, для ИКМ-30

Расчет среднего времени поиска циклового синхронизма пцс оказывается довольно сложным, поскольку при этом приходится учитывать также и структуру синхрогруппы. Дело в том, что кодовые слова различной структуры по-разному группируются в цифровом потоке. Так, комбинации вида 111 ...1 или 000...0, накладываясь друг на друга образуют пакеты максимальной длительности. Действительно, если использовать в качестве синхросигнала кодовое слово 111...1, то вероятность появления второго такого же вслед за первым при сдвиге на один тактовый интервал равна 1/2(если вероятности появления «1» и «0» одинаковы). Кодовые слова вида 011...1 или 100...0 длиной b символов образуют пакеты наименьшей длительности, так как второе такое же слово может появиться не ранее, чем через b символов с вероятностью (1/2)b. Кодовые слова вида 111 ...1 и длиной b символов называют словами с b критическими точками, а слова, которые не могут перекрываться - с одной критической точкой.

Среднее количество b-разрядных кодовых слов различной структуры в случайном цифровом сигнале одинаково, поэтому в процессе поиска синхросигнала слова с b критическими точками будут встречаться реже других из-за тенденции образовывать пакеты. Следовательно, поиск таких синхросигналов в зоне случайного сигнала будет происходить довольно быстро, так как вероятность появления ложного сигнала такого вида невелика. Однако в зоне перекрытия, когда проверяемая группа содержит часть символов синхросигнала, скорость поиска резко уменьшается.

Пусть синхросигнал имеет вид 1111, а испытываемая группа содержит три символа синхросигнала и один символ, принадлежащий случайному сигналу (рис. 2.13, а). С вероятностью 0,5 этот символ соответствует «1». С этой же вероятностью будет опознан ложный синхросигнал и начнется проверка его на истинность, которая требует времени, равного периоду посылки синхросигнала. Если же синхросигнал имеет вид 0111 (рис. 2.13, б), то вне зависимости от того, каким будет символ, принадлежащий случайному сигналу, формирования ложного синхросигнала не произойдет. Однако поиск комбинаций такого вида в зоне случайного сигнала относительно замедлен, поскольку они появляются относительно часто при случайном сочетании символов цифрового потока.

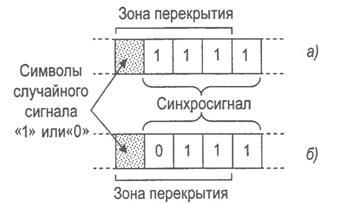
Рис. 2.13. Поиск синхросигнала в зоне перекрытия:

а — синхросигнал с 4-мя критическими точками; б — синхросигнал с одной критической точкой

Суммарное время поиска синхросигнала складывается из времени поиска в зоне случайного сигнала и времени поиска в области перекрытия. Следовательно, для минимизации среднего времени поиска циклового синхросигнала пцс надо оптимизировать структуру его кодового слова.

Для этого можно воспользоваться формулами для определения полного среднего времени поиска синхрогруппы с одной и b критическими точками, полученными на основе анализа вероятности появления этих групп в зоне случайного сигнала и в зоне перекрытия. Для синхрогруппы с одной критической точкой это время составит

 (2.6)

здесь а — число символов в потоке между соседними синхросигналами; b — число символов в синхрогруппе; Т — период повторения синхросигнала.

Для синхрогруппы с b критическими точками среднее время поиска составит

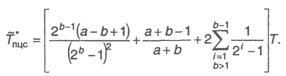 (2.7)

В формуле (2.7) приняты те же обозначения, что и в (2.6).

На рис. 2.14 приведены графики, полученные с помощью формул (2.6) и (2.7). Время поиска на графике выражено в количестве периодов передачи синхросигнала, т.е.

Для первичной ЦСП, где длительность цикла 125 мкс, синхросигнал передается через цикл (Т= 250 мкс), а цикловой синхросигнал состоит из 7 символов (b = 7), число а = 256·2 - 7 = 505, поскольку число символов в цикле равно 256. Из рисунка видно, что в этом случае относительное время поиска для структуры с одной критической точкой составит около 5 (точное значение 4,93), а для структуры с b критическими точками — около 6,1 (точное значение 6,14). Поэтому в первичной ЦСП выбран синхросигнал вида 0011011, т.е. со структурой с одной критической точкой, а абсолютное среднее время поиска составляет

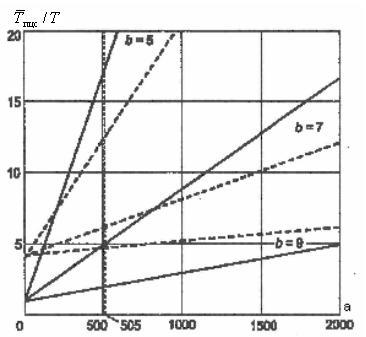
Рис. 2.14. Среднее время поиска циклового синхросигнала: - - - одна критическая точка; - - b критических точек

Подставляя результаты расчетов для ИКМ-30 в формулу (2.5), получаем

При потере синхронизма плезиохронной цифровой системой, находящейся на более высокой иерархической ступени, может произойти потеря синхронизма и во всех подчиненных системах. Таким образом, время вхождения в синхронизм низшей (первичной) системы увеличится на время последовательного вхождения в синхронизм всех систем высшего порядка, а так как при этом связь будет прервана, потери информации могут оказаться значительными. Заметим, что время удержания синхронизма для систем низших ступеней будет снижаться за счет конечного времени удержания синхронизма в системах высших ступеней. Эти зависимости являются одним из неустранимых недостатков плезиохронной цифровой иерархии.