Метод электра.

Рассмотрим теперь пример метода многокритериальной оптимизации, относящегося к другой группе - обозначенной нами на классификационной схеме как «апостериорное выявление предпочтений на эффективном множестве». Это - так называемые методы ЭЛЕКТРА, предложенные известным специалистом по ТПР профессором Б. Руа (Франция).

Цель применения методов ЭЛЕКТРА - сужение паретовского множества альтернатив. Делается это так. Для каждого из критериев (предполагается, что они - числовые) определяется по результатам опроса ЛПР «вес» - число, характеризующее важность соответствующего критерия. Во всех модификациях метода ЭЛЕКТРА делается попытка получения от ЛПР информации качественного характера об относительной важности критериев (высказывания типа «критерии 3 и 4 имеют одинаковую важность и рассматриваемые совместно имеют большую важность, чем критерий 1») и преобразования ее в количественную, числовую. Проблема здесь состоит в том, что сделать это можно в общем случае множеством способов.

Далее, для каждой пары сравниваемых альтернатив x=(x₁,.....,x_n) и y=(y₁,.......,y_n) (где n - число критериев, а для дальнейшего мы через I обозначим множество критериев, т.е. I= n) выполняются такие действия. Множество I разбивается на 3 подмножества:

I⁺(x,y) - множество критериев, по которым х превосходит у: x>y.

I^- (x,y) - множество критериев, по которым у превосходит х: у>х.

I⁼(x,y) - множество критериев, по которым х и у имеют одинаковые оценки: у=х.

Определяется относительная важность PPP каждого из этих подмножеств:

( ,  ,)

P_i. - коэффицент относительной важности i-го критерия. Теперь мы готовы сформировать правило сравнения альтернатив х и у:

- в методе ЭЛЕКТРА-I оно таково:

, .

- в методе ЭЛЕКТРА-II оно модифицировано:

, (c ₂1).

Всё рассмотренное до сих пор весьма традиционно, и содержит традиционную погрешность в логических рассуждениях: получается, что очень маленький выигрыш по одному критерию может компенсировать очень большой проигрыш по другому. Для того чтобы эту трудность (погрешность) исключить, в методе «Электра» пытаются НЕ сравнивать очень сильно различающиеся альтернативы. Они просто объявляются несравнимыми. Вводится так называемый «индекс несогласия»:

х и у несравнимы, если d_xy d,

где d_xy - расстояние между х и у определяется как max_ix_i - y_i, a d - т.н. порог индекса несогласия. Теперь введённые нами раньше соотношения модифицируются так:

в ЭЛЕКТРА-I

.

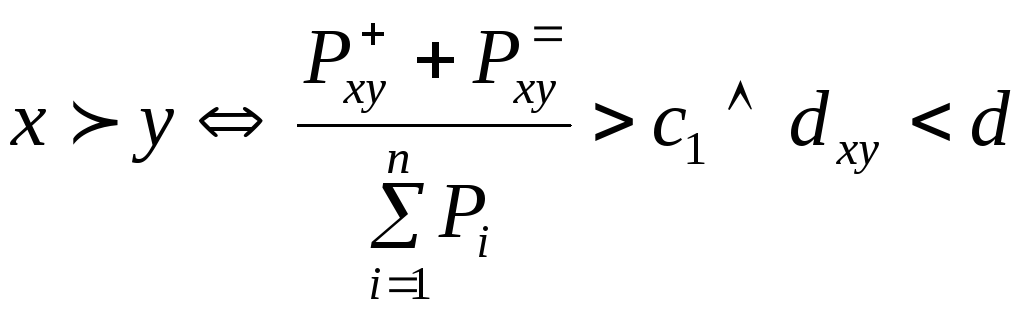в ЭЛЕКТРА-II

.

Получаемое бинарное отношение, очевидно, уже не будет обладать свойством полноты. Это учитывается и в окончательном результате ЭЛЕКТРА. Он таков. В исходном паретовском множестве выделяется т.н. ядро, состоящее из недоминируемых по новому (описанному нами) бинарному отношению элементов и всех, несравнимых с ними (т.е. любой элемент, не вошедший в ядро, доминируется хотя бы одним элементом ядра). Отметим, что, к сожалению, нельзя гарантировать цикличность отношения, получаемого описанным способом.

Принятие решений на основе метода анализа иерархий (МАИ).

Метод анализа иерархий так же относится к многокритериальным методам принятия решений. Его преимущество заключается в простоте используемой экспертизы, которая предполагает декомпозицию существующей проблемы на все более простые составляющие части. В результате такой процедуры определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии, выражаемая численно в виде векторов приоритетов. Следует отметить, что получаемые таким образом оценки являются жесткими, поскольку измеряются в шкале отношений.

Существует ряд модификаций МАИ, которые определяются характером связей между критериями и альтернативами, расположенными на нижнем уровне иерархии, а также методами сравнения альтернатив. В настоящем учебном пособии рассматривается наиболее общий и несколько упрощенный вариант метода анализа иерархий.

Построение иерархии начинается с исследования проблемы. Далее строится собственно иерархия, включающая цель, расположенную в вершине, промежуточные уровни (например, критерии), и альтернативы, расположенные на нижнем уровне. На рис. приведены три типовых варианта отображения одной иерархии.

E¹₁

E¹₁

E¹₁

E²₁

E²₂

E²₁

E²₁

E²₁

E²₂

E³₁

E³₁

E³₁

E³₂

E³₃

E³₁

E³₂

E³₃

E³₂

E³₂

E³₃

E³₃

А.- декомпозиция; Б. – синтез В – упорядочение Рис. Виды иерархии.

Для установления относительной важности элементов иерархии используется шкала отношений (табл. ), позволяющая численно оценить степень предпочтения одного сравниваемого объекта перед другим.

Таблица .

Степень значимости vij	Определение	Объяснение
1	Одинаковая значимость	Два действия вносят одинаковый вклад в достижение цели
3	Некоторое преобладание значимости одного действия над другими (слабая значимость)	Имеются некоторые соображения в пользу предпочтения одного из действий, но недостаточно убедительные
5	Существенная или сильная значимость	Имеются надежные суждения или логические выводы для предпочтительности одного из действий
7	Очень сильная значимость	Существуют убедительные свидетельства в пользу одного действия перед другим
9	Абсолютная значимость	Степень предпочтительности устанавливается абсолютно
2,4,6,8	Промежуточные значения между двумя соседними суждениями	Для ситуации, когда необходимо компромиссное суждение
Обратные величины 1/vij	Если действие i при сравнении с действием j получило некоторую оценку степени значимости, то действию j при сравнении с i приписывается обратное значение	При сопоставлении двух действий в обратном порядке значение шкалы vij приобретает обратную величину 1/vij

При сравнении двух действий следует задавать следующие вопросы:

• Какой критерий важнее или имеет большее воздействие?

• Какая альтернатива является предпочтительнее?

После построения иерархии устанавливается метод сравнения ее элементов. Наиболее распространенным является метод попарного сравнения. При его использовании сравнения проводятся в терминах доминирования одного элемента над другим и оцениваются с помощью девяти бальной шкалы (табл. ) В результате строится множество матриц парных сравнений. Каждая матрица Е имеет следующий вид :

где a_ij = v_i/v_j и a_ji = 1/a_ij, n – порядок матрицы парных сравнений.

Исходя из этих условий вполне очевидно, что ЛПР выносит n(n-1)/2 суждений.

Для каждой матрицы парных сравнений рассчитываются собственные вектора (W^E)- вектора приоритетов по следующему алгоритму:

• Вначале находим оценки компонент собственного вектора по строкам

• Д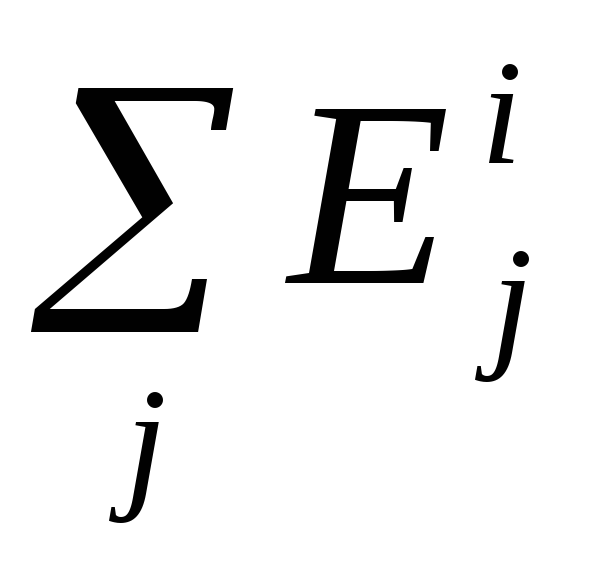алее находим сумму всех компонент столбца

• Полученный результат нормализуем

Соответственно, для каждой полученной матрицы следует оценить:

• максимальное собственное значение _max по формуле

где e^T – единичный транспонированный вектор;

W^E – собственный вектор матрицы парных сравнений.

• Однородность суждений путем расчета

• индекса однородности (ИО) = (_max – n)/(n-1)

• отношения однородности (ОО) = ИО/M(ИО), где М(ИО) – среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений. Имеет табличное значение [ c.39]. Величина ОО должна быть порядка 10% или менее, чтобы быть приемлемой. В противном случае следует перепроверить предоставленные суждения.

Матрицы парных сравнений строятся для

• сравнения относительной важности критериев на втором уровне (s=2) по отношению к общей цели на первом уровне (s=1);

• сравнения относительной важности критериев – “потомков” уровня s (s=3m, где m – номер уровня иерархии) по отношению к критерию – «родителю» уровня s-1)

• сравнения относительной важности каждой альтернативы по отношению к критериям предпоследнего уровня иерархии.

Поскольку мы можем иметь в иерархии несколько уровней, то к собственным векторам следует применять принцип иерархического синтеза, который заключается в последовательном определении векторов приоритетов альтернатив относительно элементов Eⁱ_j,находящихся на всех иерархических уровнях, кроме предпоследнего. Здесьi– уровень иерархии,j – порядковый номер элемента на уровне. Вычисление векторов приоритетов осуществляется по направлении от нижних уровней к верхним с учетом конкретных связей между элементами, принадлежащих различным уровням.