МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИИ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ

ИНСТИТУТ ИНФОРМАЦИОННЫХ СИСТЕМ УПРАВЛЕНИЯ

Домашняя работа № 3

По дисциплине

ПРОГНОЗИРОВАНИЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ

Студента: Голуба А.А.

Специальность: Математические методы и исследование операций в экономике

Курс: IV

Группа: I

Преподаватель: Писарева О.М.

Москва 2001

По данным условиям составим прямую задачу производственного планирования:

Двойственная задача будет иметь следующий вид:

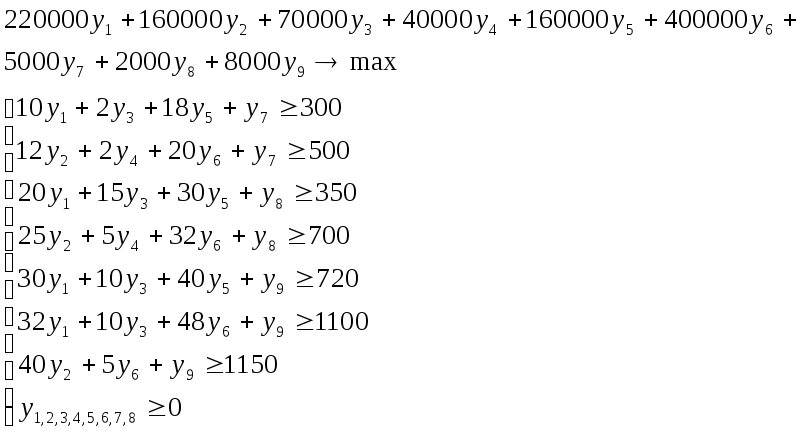
Прямую задачу будем решать с помощью пакета решения задач линейного программирования BLP. Результаты решения следующие ( Приложение 1): получили оптимальное и единственное решение –

X_опт=( х₄, s₂, х₆, s₄, х₅, s₆, х₁, x₃, х₇)=(1302, 5566, 3726, 33491, 1226, 164236, 5000, 698, 3047).

Теперь найдем обращенный базис B^-1

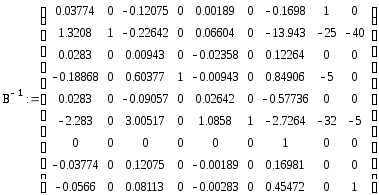
Анализ влияния изменения вектора правых частей ограничений (b)

Допустим, что предприятие увеличивается количество стандартного сырья на 100000, и s2 на 40000. Пусть b(w)=b+w*d, где

w- масштаб изменений,

d - заданный приростной вектор – структура изменений.

Cформируем приростной вектор d, имеющий следующий вид:

Следовательно, вектор правых частей ограничений приобретет вид:

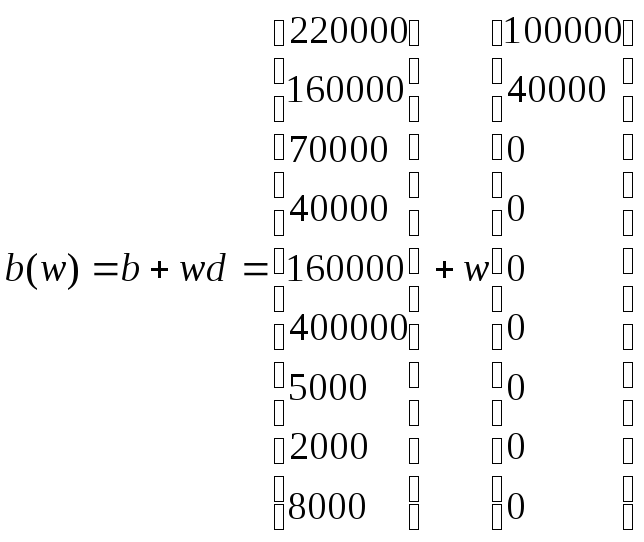
Найдем вектор  равный :

Определим зависимость компонент оптимального плана от w, используя следующую формулу для базисных и небазисных переменных:

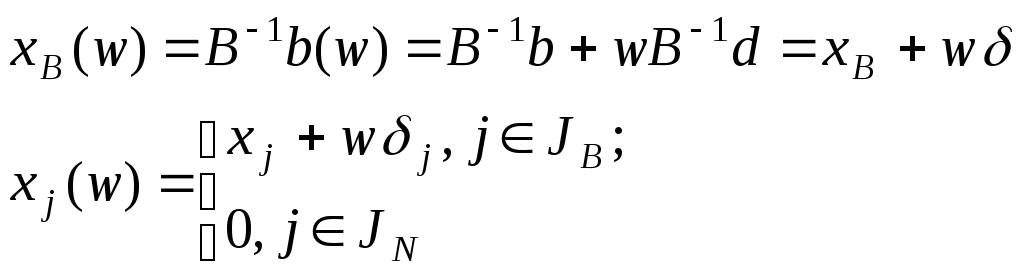
Таким образом, получаем:

Двойственные переменные не зависят от вектора b, т.к. y_i=c^T_B(B^-1), поэтому теперь найдем зависимость оптимального значения (минимума) целевой функции от w:

L (w) =c^T_BX_B(w)=L + w* c^T_B* = L+ w y^T d = 11141981+1143000000w

Допустимые границы изменения w определяются условиями допустимости и оптимальности базиса. Определим границы изменения w, в которых истинны выше найденные зависимости. По следующей формуле определим подмножества базисных индексов:

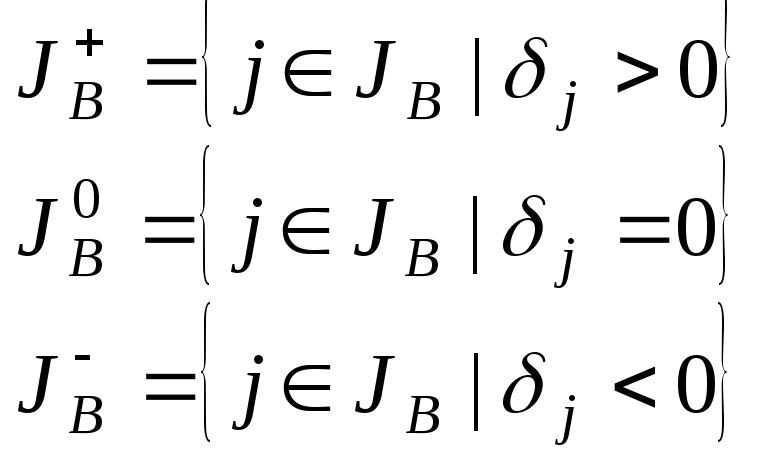
Получим:

Найдем границы по следующим формулам:

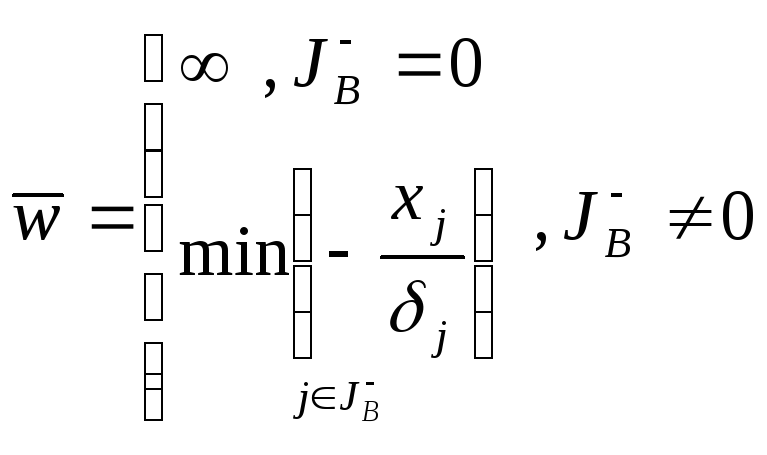
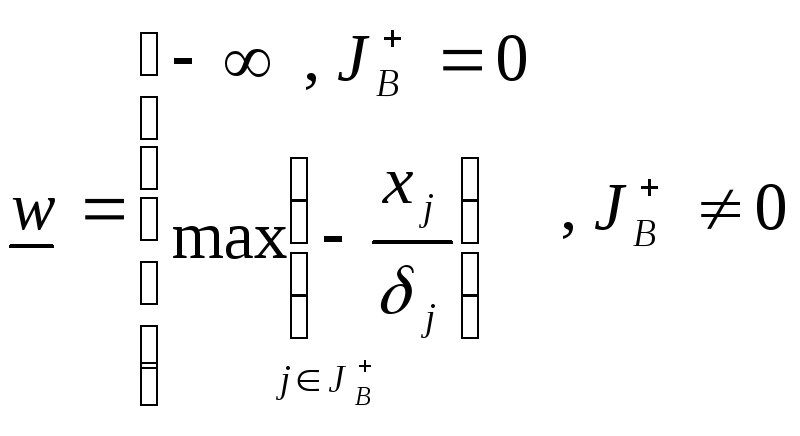(1.1)

В результате получаем, что

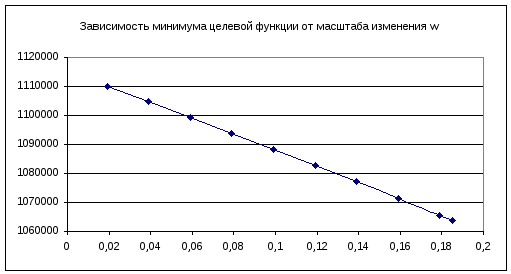
Проанализируем влияние масштаба изменений на оптимальный план и на минимум целевой функции:

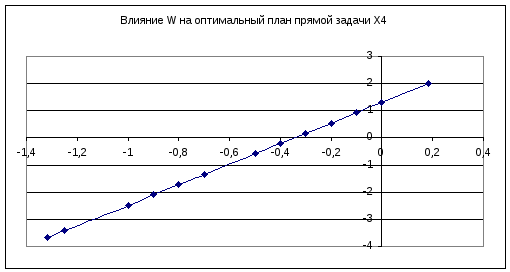
Анализ влияния изменения целевой функции

Предположим, что цена на продукцию А увеличилась на w руб, значит, должны увеличиться и удельные затраты – увеличится общие затраты (целевая функция). Необходимо проследить влияние изменения цены на выпуск продукции работы.

Пусть c (w) = c + wg , где g – приростной вектор-столбец. Приростной вектор в данном случае будет иметь вид:

g = (-10, 0, -20, 0, -30, -32, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)^T,

причем

g^Т_В = (x4, s2, x6, s4, x5, s6, x1, x3, x7) = (0, 0, -32, 0, -30, 0, -10, -20, 0), где

g^Т_В – часть вектора g , соответствующая базисным переменным

С учетом изменения цены сборочно-наладочных работ целевая функция принимает следующий вид:

L= (300-10w)x₁ + 500 x₂ + (350-20w) x₃ + 700 x₄+ (720-30w)x₅ + (1100-32w)x₆+ 1150 x₇

Вычислим вектор  :

^Т = g^Т_В B^-1

^T = (-1 0 0,00034 0 -0,00024 0 0,00012 0 0)

Необходимо найти зависимость компонент оптимального плана от изменения цены на сборочно-наладочные работы. Для оптимального плана прямой задачи справедлива формула:

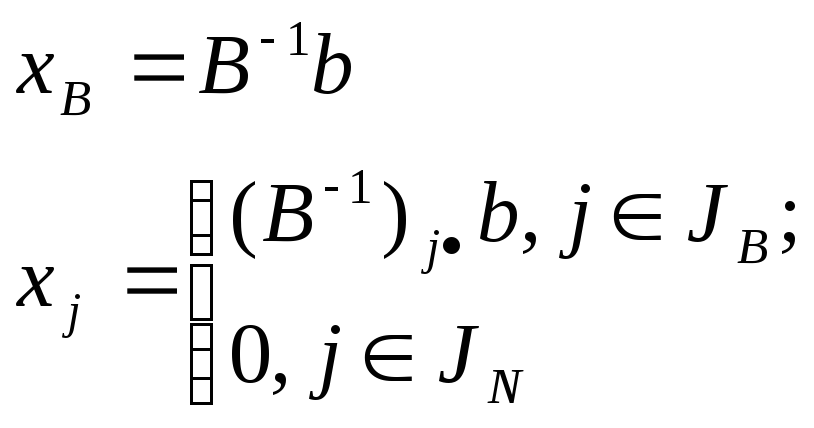
следовательно, оптимальный план прямой задачи не изменится при изменении целевой функции, значит не изменится и выпуск изделий.

Воспользуемся формулой для оптимального значения (минимума) целевой функции:

и найдем зависимость максимума прибыли от w:

L(w) = 1114981 – 39870w

По следующей формуле найдем зависимость двойственных переменных от масштаба изменений:

y2=y4=y6=0

y1=-0,3774 - w

y3=-3,792+0,00034w

y5=-9,519-0,00024w

y7=482,7+0,00012w

y8=700

y9=1150

Теперь определим границы w, в которых справедливы полученные зависимости. Границы изменения w определяются в этом случае условием, оптимальности плана (базиса). Вычислим:

Получаем условие:

Разобъем множество J_N на три непересекающихся подмножества по формуле:

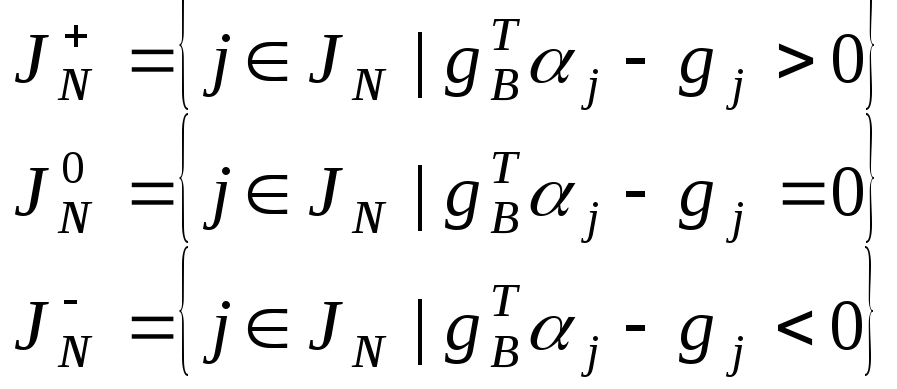
значение выражений для этой формулы сведем в таблицу:

	j
X2	2	0*0,00012-0=0
S1	8	-20*(-1)-0=20
S3	10	0*0,00034-0=0
S5	12	0*(-0,00024)-0=0
S7	14	0*(-0,00012)-0=0
S8	15	0-0=0
S9	16	0-0=0

И получим, что:

По формулам

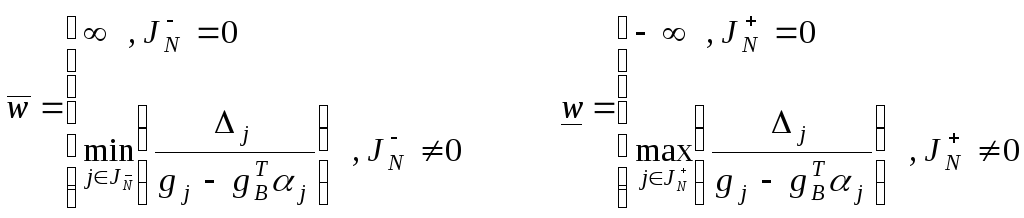
Для данных условий получаем следующие границы:

Итак : w  [0,01887 ; ]

Проанализируем влияние границ масштаба изменения на оптимальный план двойственной задачи и минимум целевой функции:

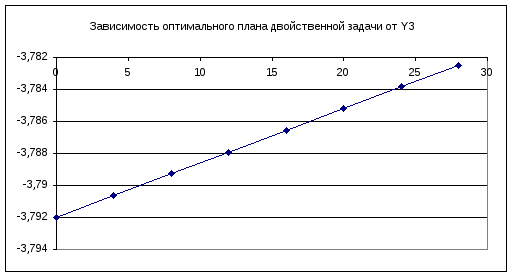
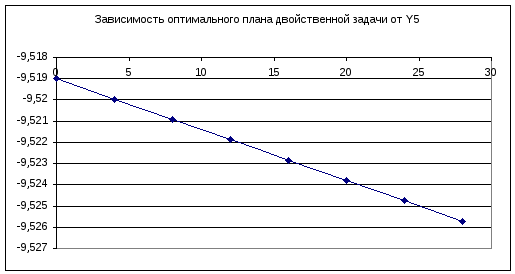
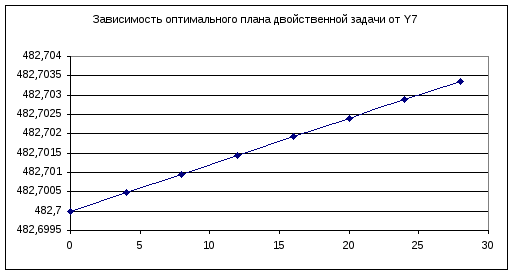
Анализ влияния одновременного изменения столбца правых частей

ограничений и целевой функции

Пусть c (w) = c + wg и b (w) = b + wd

Зависимость x (w) определяется по формуле:

Зависимость y (w) определяется по формуле:

Найдем зависимость L(w) оптимального значения целевой функции:

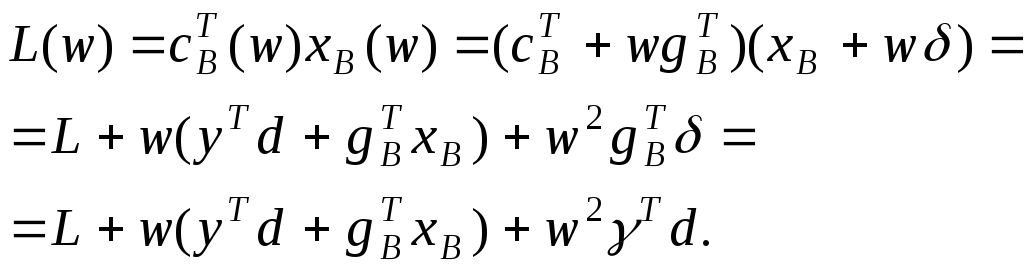
Так как:

g^Т_В = (0, 0, -32, 0, -30, 0, -10, -20, 0)

^T = (-1, 0, 0.00034, 0, -0.00024, 0, 0.00012, 0, 0)

d^T = (100000, 40000, 0, 0, 0, 0, 0, 0, 0)

y^T = (-0.3774, 0, -3.792, 0, -9.519, 0, 482.7, 1.144, 700, 1150)

следовательно, получим следующую зависимость L (w):

L (w) = 1114981 - 257700w -99980w²

Ввиду того, что в данном случае при изменении w могут быть нарушены и допустимость, и оптимальность плана, поэтому при определении границ w надо учитывать оба условия:

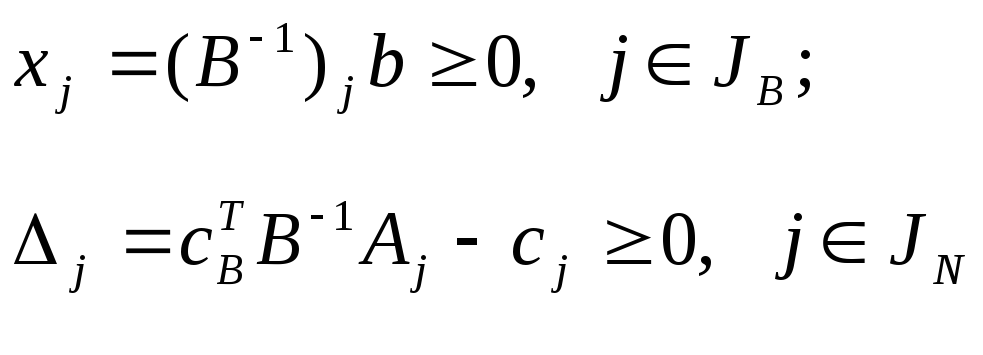
Д ля соблюдения данных условий необходимо, чтобы выполнялись сразу два условия оптимальности и допустимости, т.е. надо найти пересечение множеств, которые представлены формулами (1.1. и 1.2.).

Для данного случая получаем, что:

Анализ влияния изменения строки ограничений

Пусть A_r(w) = A_r + w l^T и b(w)=b+w*d,

где l^T – приростной вектор-столбец.

l^T=(0,0,10,0,0,0,0,0,0,0,0,0,0,0,0,0)

A_r(w)=(10,0,20,0,30,32,0,0,0,0,0,0,0,0,0,0)+w(5,0,10,0,0,0,0,0,0,0,0,0,0,0,0,0)

^T = l_B^T B^-1 , где l_B = (l₁ ,…., l_m)^T – часть вектора l, соответствующая базисным переменным

l_B^T = (0, 0, 0, 0, 0, 0, 0, 10, 0)

^T = l_B^T B^-1 = ( -0.377, 1.208, 0, -0.019, 0, 6.698, 0, 0)

После определенных вычислений получаем следующие формулы:

1. для оптимального плана прямой задачи

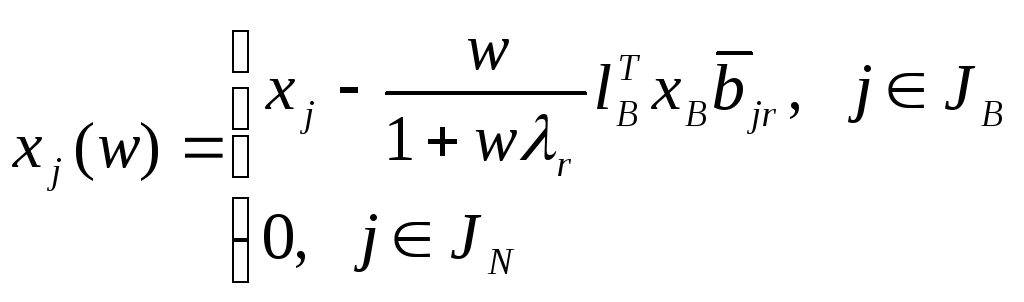
2. для оптимального плана двойственной задачи получаем:

3. для оптимального значения целевой функции после вычислений получаем:

L=1114981-2634*w/(1-0.377w)

_r = -0,377 , значит, w > 2,65 y_r = -0,3774

Найдем множество допустимых значений w.

Разобьем множество базисных индексов на 3 непересекающихся подмножества:

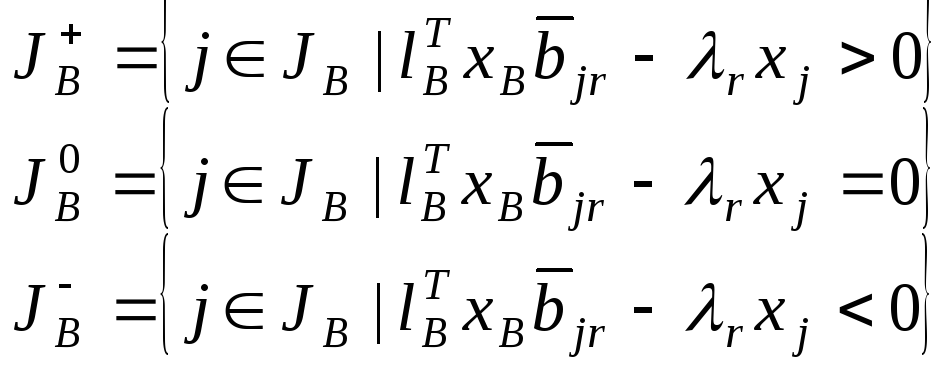
	J
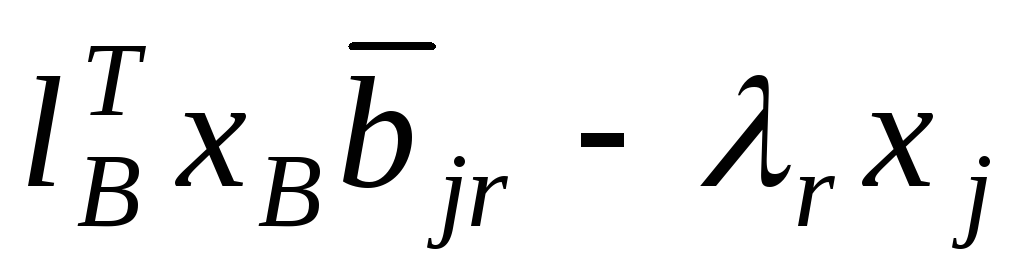
X4	1	1697
S2	2	44340
X6	3	2310
S4	4	6592
X5	5	1367
S6	6	-11090
X1	7	1885
X3	8	-942.854
X7	9	-611.281

Найдем границы w:

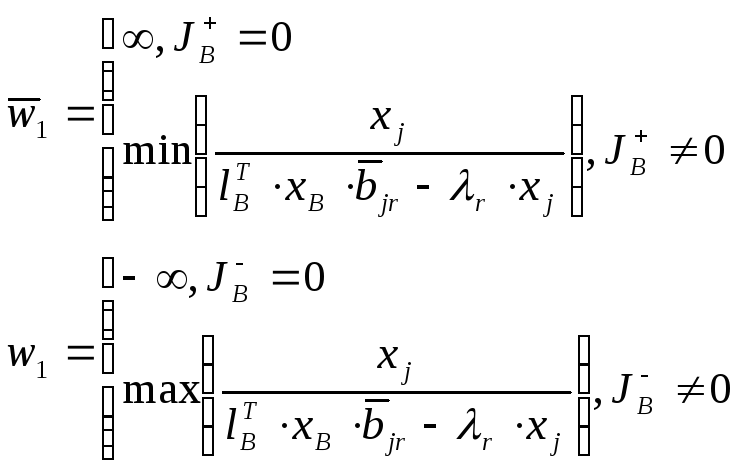
Разобьем множество небазисных индексов на 3 непересекающихся подмножества:

	j
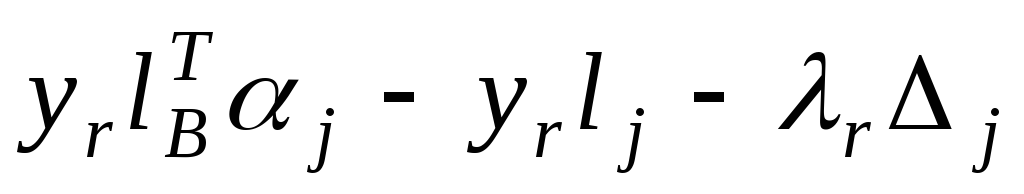
X2	1	-6.522
S1	2	-0.142
S3	3	-1.43
S5	4	-3.588
S7	5	-181.974
S8	6	-263.9
S9	7	-433.55

Найдем границы w:

В итоге получаем: