Представление древовидных н сетевых структур в памяти эвм

Древовидные структуры. При физической организации древо­видных структур данных в памяти ЭВМ необходимо решить два вопроса :

1) как организовать данные, представленные вершинами (узла­ми древовидной структуры) ;

2) как организовать связи между данными, представленные в схеме БД дугами древовидной структуры.

Для упрощения считаем, что данные в узле структуры можно представить последовательным списком элементов фиксированного размера, т. е. записями фиксированной длины. Поэтому рассмот­рим способы организации связи между узлами в древовидной структуре данных.

Древовидная структура - это связный неориентированный граф, который не содержит циклов. Рассмотрим еще два вспомогательных определения. Разбиением 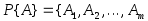} множества называется множество подмножеств(причем, ) та­ких, что их объединение есть множество А и они являются попарно непересекающимися:

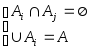для любых i не равных j

Вложенным множеством называется непустой набор } непустых множеств таких, что для любых двух множеств выполняется одно из следующих трех условий:

Таким образом, разбиение исходного множества и возможные последующие уточнения этого разбиения могут образовывать вло­женное множество.

Деревья, эквивалентные набору вложенных множеств, назы­вают ориентированными деревьями. Если линейно упорядочить элементы, то произойдет линейное упорядочение всех классов эквивалентности. В этом случае получают упорядоченное де­рево. Поскольку получена линейная упорядоченность множества В, упорядоченное дерево можно представить линейным списком.

Двоичным (бинарным.) деревом называется упорядоченное де­рево, в котором:

1) каждый произвольный узел, кроме концевого, имеет не бо­лее двух исходящих узлов (потомков или сыновей);

2) каждый сын произвольного узла идентифицируется как ле­вый или правый сын.

Поддерево Т, корнем которого является левый сын узла и, называют левым поддеревом узла v. Поддерево Т, корнем кото­рого является правый сын узла v, называют правым поддеревом узла v. Все узлы в Т располагают левее всех узлов в Т, т. е. при представлении двоичного дерева считают, что множество сы­новей каждого узла упорядочено слева направо.

Обобщением двоичных деревьев является сбалансированное (или регулярное) дерево. В сбалансированном дереве количество исходящих узлов из любого произвольного узла может быть больше двух, однако обязательно из каждого произвольного узла (кроме концевого) исходит одинаковое количество порожденных узлов. Процесс включения новых узлов в сбалансированное дерево вы­полняется сверху вниз, а на каждом уровне дерева- слева на­право. Сбалансированные деревья используются для построения индексов файлов.

Сбалансированное дерево называется полным, если для неко­торого целого числа k каждый узел глубины, меньшей, k имеет r исходящих узлов и каждый узел глубины k является концевым узлом. Глубина узла v в дереве -это длина пути из корня в v. Высотой узла v в дереве называется длина самого длинного пути из v в один из концевых узлов. Уровень узла v в дереве равен разности между высотой дерева и глубиной узла v (уровень кон­цевых узлов имеет номер 0, следующий уровень- 1 и т. д.).

Количество узлов полного сбалансированного дерева высо­ты k:

где г - количество исходящих узлов. В случае двоичного дерева r=2 и формула упрощается:

Методы представления древовидных структур линейным спис­ком с последовательным распределением памяти.

Метод ис­пользования адресной арифметики. Метод хорошо применим к сбалансированным (регулярным) деревьям. В этом случае узлы представляются записями фиксированной длины. Пусть для размещения одного узла дерева требуется квант па­мяти размером т единиц.

Первый способ. В имеющемся векторе памяти А в первом кван­те А[1] с адресом помещают корень дерева. Кванты

заполняют непосредственными потомками корня дерева. После­дующие r квантов заполняют непосредственными потомками узла, размещенного в кванте А[2]. Далее г квантов заполняют непосред­ственными потомками узла, размещенного в кванте A[3], и т. д.

Адрес k-го кванта А[k] вычисляют по формуле:

В зависимости от значения г определим функциональную за­висимость между адресами квантов, в которых размещаются узел и его непосредственные потомки.

Для случая г=2. Этот вариант рассмотрен в (списковые структуры)

Для случая r=3. Непосредственные потомки кванта A[k] это кванты A[3k-1], A[3k] и A[Зk+1] с адресами

Чтобы получить адрес узла, являющегося исходным для узла, размещенного в кванте А[k], необходимо k разделить на 3 и округ­лять до целого значения по общим правилам округления. Адрес определяют по формуле

Для случая г = 4 использование данного способа несколько осложняется. Это связано с тем, что для получения адреса узла, являющегося исходным для узла, размещенного в кванте A[k], требуется разрабатывать специальный алгоритм вычисления.

Структура, полученная при данном способе представления, поз­воляет осуществлять поиск узлов в прямом (от корня) и в обрат­ном (к корню) направлениях.

Второй способ. Применим только для двоичных сбалансирован­ных деревьев. Если используется вектор памяти от кванта i до кванта j включительно, то корень дерева помещается в квант A[l] где

т. е. в середину вектора памяти. В квантах памяти от i до (l-1) включительно размещается левое относительно корня поддерева а в квантах от (l+1) до j включительно -правое относительно корня поддерево. Размещение поддеревьев выполняется аналогич­но, корень левого поддерева размещается в квант

корень правого поддерева - в квант

Адреса квантов вычис­ляются по формуле . Структура, полученная при данном способе представления, приспособлена для поис­ка узлов в прямом направ­лении.

Рассмотренная струк­тура еще называется де­ревом сравнений, посколь­ку используется для орга­низации данных при логарифмическом или бинарном поиске.

Метод использования левосписковых структур. Метод строит последовательность узлов при обходе исходной древовидной структуры сверху вниз и слева направо. Алгоритм по­строения последовательности в данном методе следующий. Выби­раются узлы, начиная от корня дерева и до концевого узла включительно по крайней левой ветви дерева, затем осуществляется подъем вверх до первой следующей ветви, и процесс повторяется. Узлы, ранее выбранные, в последовательность не включаются.

Схема обхода дерева:

7.12

В результате обхода дерева получим такую последовательность узлов: (аб1в1г1в1г2в1г3в1б1в2г4в2б1аб2в3г5в3г6в3б2в4г7в4б2аб3в5г8).

Затем удалим ранее выбранные узлы и получим левосписковую структуру: (аб1в1г1г2г3в2г4б2в3г5г6в4г7б3в5г8).

Метод левосписковых структур применим для любой древовид­ной структуры. При размещении полученной последовательности в памяти можно использовать либо специальные разделители (а(б1(в1(г1г2г3)в2(г4)б2(в3(г5г6)в4(г7))б3(в5(г8)))), либо в каждой записи резервировать поле, в котором указывается номер уровня. Метод левосписковых структур реализует последовательный дос­туп к узлам дерева в прямом и обратном направлениях.

Методы представления древовидных структур свя­занными линейными списками.

Метод указателей на порожденные записи. Метод реализует движения по дереву в прямом направ­лении. В случае исполь­зования этого метода лю­бая запись, кроме запи­сей самого нижнего уров­ня, должна иметь столько указателей, сколько имеет­ся порожденных записей.

Метод указателей на исходные записи. Указа­тели на исходные записи используются для организации прохода по дереву в обратном направлении - от концевых узлов к корню. Этот метод используется в комбинации с другими ме­тодами.

Метод указателей на порожденные и исходные записи. Данный метод обеспечивает прохождение дерева как в прямом, так и в обратном направлении, поскольку используется двунаправленный список. Недостаток метода тот же, что и у метода указателей на порожденные записи, т. е. количество указателей в узлах переменно и определяется числом порожденных записей. Только для случая сбалансированных древовидных струк­тур количество указателей становится постоянным.

Метод указателей на порожденные и подобные записи. Метод обеспечивает прохождение дерева в прямом направлении. Достоинством данного метода по сравнению с мето­дом указателей на порожденные записи является ограниченное количество указателей - по од­ному указателю в концевых узлах и по два в остальных. Однако с увеличением числа подоб­ных записей время доступа к за­писям возрастает за счет после­довательного доступа по цепочке указателей.

Метод указателей на порожденные, подобные и исходные записи. Метод обладает достоинствами и недо­статками предыдущего метода), однако реализует прохождение дерева в обратном направлении.

Метод кольцевых структур. Однонаправленные цик­лические списки позволяют представить исходную древовидную структуру, включив в каждый узел по два указателя: порожденных записей, подобных записей. Время доступа к записям в данном методе примерно такое же, как в методе указателей на порожденные и подобные записи.

Следует отметить, что чаще используются двунаправленные циклические списки. В этом случае общее количество указателей в каждом узле соответственно возрастает до четырех -для обхода в прямом и обратном направлениях как по кольцам порож­денных записей, так и по кольцам подобных записей.

Метод справочников. В данном методе указатели уда­ляются из записей и организуются в специальные файлы-спра­вочники. Достоинство метода заключается в том, что справочники, поскольку в них хранятся только указатели, обычно по размеру существенно меньше основных файлов, в которых хранятся записи исходных данных. Поэтому справочник можно считывать в оперативную память ЭВМ и всю обработку связей выполнять с использованием только оперативной памяти, а затем уже требуемые ис­ходные записи считывать из внешней памяти. Ис­пользование справочников существенно повы­шает скорость поиска данных. Кроме того, справочники можно ор­ганизовать с ориентацией на определенные типы запросов.

Для представления де­ревьев применяют раз­личные комбинации. Для конкретных типов древовидных структур методы их физического представления выбираются исходя из условий использования дан­ных в информационной системе и имеющихся технических уст­ройств памяти.

Сетевые структуры. Для представления сетевых структур ис­пользуют рассмотренные выше методы, но в определенной комби­нации, позволяющей реализовать сетевую структуру. Например, используют комбинацию методов с указателями на порожден­ные, подобные и исходные записи. Наиболее часто используют кольцевые структуры.

В случае, если количество указателей в записях ограничено, то реализуют только относительно несложные сетевые структуры. Для сложных сетевых структур необходимо вводить для каждой записи переменный список указателей. Однако использование встроенных (в записи) списков указателей переменной длины вызывает серьезные проблемы при создании соответствующих обслуживающих программ. Например, для решения задачи об­новления файла должна быть возможность сжатия и расширения списков указателей (одни связи между записями добавляются, другие устраняются). Поскольку эти указатели встроены в запись, меняются размеры памяти. Поэтому необходимо либо заранее отводить для хранения каждой записи поле памяти, рассчитан­ное на определенное увеличение числа указателей (при этом не­обходимо реализовать возможность добавления участков перепол­нения, если поле заполняется), либо выполнять реорганизацию файла при выполнении изменений в записях. Но в последнем случае выполняется физическое перемещение записей в памяти, что приводит к необходимости изменять значения полей указателей в записях. Задача упрощается, если использовать символические указатели, но при этом возрастает время обработки.

Сложность и трудоемкость организации и использования запи­сей со встроенными указателями переменной длины приводит к целесообразности использования метода справочника (как и для древовидных структур).

Указатели изымаются из записей в сетевых структурах, раз­мещаются в отдельном файле -справочнике. Справочник можно организовать оптимальным образом, чтобы поиск данных в соответствующем разделе выполняется быстрее. Чем сложнее структура данных, тем более целесообразно применять справочник.

Методы организации и обработки файлов

Данные хранятся во внешней памяти на магнитных дисках, маг­нитных лентах и т. д., а их обработка выполняется в оператив­ной памяти ЭВМ. Поэтому при обработке некоторые порции дан­ных пересылаются из внешней памяти в оперативную либо наобо­рот.

Модель внешней памяти. При больших объемах данных в БД порядка байт может потребоваться несколько томов внешней памяти (несколько пакетов дисков, бобин магнитных лент). Однако обмен между внешней н оперативной памятью вы­полняется небольшими порциями данных -обычно объемом не более нескольких сотен байт. С этой целью внешняя память раз­бивается на части, называемые блоками или страницами. Данные пересылаются блоками. Операцию пересылки еще называют об­меном данными между внешней и оперативной памятью. Обмен между внешней и оперативной памятью называется чтением бло­ка, а в обратном направлении -записью блока.

При чтении блока, последний помещается в оперативной па­мяти в специально отведенный (буферный участок памяти). Может отводиться участок под несколько буферов (буферный пул). Чем больше буферный пул, тем эффективнее обработка данных. При считывании другого блока из внешней памяти в тот же самый буфер предыдущее содержимое буфера теряется. При внесении изменений в блок вначале блок считывается в буфер, затем вы­полняются изменения и далее блок записывается во внешнюю память.

Для организации каждого файла в зависимости от его размера во внешней памяти ему выделяется от одного до n блоков, где размещаются записи файла. Предположим, что в одном блоке размещаются записи только одного файла. В зависимости от соот­ношения объемов записей и блоков может оказаться, что в одном блоке размещается либо одна, либо несколько записей файла, либо одна запись размещается в нескольких блоках. Обычно запись занимает несколько десятков байт.

Каждый байт в блоке пронумерован: 0, 1, 2, 3, ..., Х. Номер байта блока, с которого начинается запись, определяет относи­тельный адрес записи файла в блоке.

В качестве адресов записей файла во внешней памяти исполь­зуют: машинный адрес; относительный адрес; ключ записи.

В качестве относительного адреса записи файла используют ее номер по порядку (внутрисистемный номер) в файле либо ком­бинацию таких составляющих адреса, как номер блока и относи­тельный адрес в блоке, либо номер блока и значение ключа. В последнем случае, после считывания блока в буфер оператив­ной памяти, доступ к записи в буфере осуществляется с помощью какого-либо метода поиска записей в файле по значению ключа.

При чтении записи из блока, который уже находится в буфере, обмен с внешней памятью не выполняется. Во многих системах при вводе записи ей присваивается уникальный системный иден­тификатор-ключ базы данных.

Запись обычно состоит из служебных полей, в которых хра­нятся указатели, реализующие связи с другими записями, и другая информация, необходимая для организации управления файлом, и полей хранимых данных. Записи могут быть фиксированной и переменной длины. Записи размещаются в блоках плотно, без промежутков, последовательно одна за другой. В блоке часть памяти отводится также для служебной информации о блоке: относительные адреса свободных участков памяти, указатели на следующий блок и т. д. Если файл состоит из записей фиксированной длины, то в одном блоке можно разместить k записей:

где обозначает целую часть числа;-соответственно объем блока и записи в байтах.

Однако обычно блоки заполняют не полностью, например на­половину. Оставшаяся область блока остается некоторое время при работе системы незаполненной (зарезервированной). В даль­нейшем эта область заполняется при расширении (увеличении) записей, хранящихся в блоке, или при поступлении в систему новых записей, которые в соответствии со значениями их ключей или по другим условиям необходимо поместить в одном блоке с уже хранящимися записями. По истечении некоторого времени блок заполняют полностью. Для хранения поступающих данных, которые должны были бы попасть в этот блок, выделяется до­полнительный блок памяти в области переполнения. Записи, ко­торые должны были размещаться в одном блоке, связываются специальными указателями в одну цепь. Процесс выделения до­полнительных блоков в области переполнения можно было бы не ограничивать, если бы при этом не снижалась эффективность (по временному критерию) обработки хранимых данных. Сниже­ние эффективности обработки данных связано с тем, что система непроизводительно затрачивает время на поиск записей в области переполнения, что сказывается на увеличении общего времени поиска требуемых записей (по сравнению со случаем, когда об­ласть переполнения еще не была использована и все записи были размещены в основной области). Поэтому периодически файл реорганизуется: при необходимости файлу добавляется тре­буемое количество блоков в основной области памяти и выпол­няется требуемая перекомпоновка записей. При этом исходят из расчета, чтобы можно было освободить область переполнения, а все записи разместить в блоках основной области, причем в каж­дом блоке разместить записи последовательно и в таком количе­стве, чтобы r-я часть блока осталась незаполненной. В этом случае требуемое количество блоков

где r<1 незаполненная часть блока; - количество записей в файле

Считаем, что все блоки каждого файла пронумерованы и система определяет требуемый блок по имени фай­ла и номеру блока. Если файл состоит из записей фиксированной длины, записи организованы последовательно и имеют внутри файла системный номер, то по этому номеру вычисляют номер блока, в котором находится запись:

Среднее время выполнения операции обмена зависит от типа устройства внешней памяти (от его характеристик) и от размера блока:

где - среднее время выполнения операции обмена;- время считывания, приведенное к одному байту (т. е. время считывания одного байта);-время подготовки устройства к выполнению операции обмена. Время поиска данных в файле

где - время выполнения операции поиска;- среднее время выполнения (в процессоре) одной операции сравнения;-ко­личество операций обмена;- количество операций сравнения (в оперативной памяти).

Еслито время поиска в основном определяется време­нем, затрачиваемым на обмен с внешней памятью. Поэтому при составлении алгоритмов поиска данных в файле стремятся к сокращению количества операций обмена.

На скорость поиска данных в файле наибольшее влияние оказывают следующие характеристики файла и технических уст­ройств внешней памяти, использованных для его организации: объем блока (в байтах); объем файла (в байтах); количество записей в блоке файла ; количество записей в блоке индекса; количество блоков в файле данных; доля резервируемой ча­сти блока (при начальной организации данных в файле)r, длина поля, отведенного для указателя; количество записей в файле ; число полей в записи; размер записи (в байтах), - длина ключевого поля в записи; число записей файла, удовлетворяющих условию поиска Q; среднее число блоков переполнения на один блок файла; среднее время .

Последовательный поиск. Последовательный поиск за­ключается в последователь­ной проверке всех записей файла на их соответствие условию поиска Q. Записи, значения полей которых удовлетворяют условию Q, выдаются в качестве резуль­тата поиска.

Поиск по равенству К=а, где К- значение ключевого поля. Алгоритм поиска заключается в по­следовательном просмотре записей файла и проверке выполнения условия К=а. Если запись найдена, то алгоритм заканчивает свою работу (удачный поиск). В противном случае поиск заканчивается просмотром последней записи файла (неудачей поиск).

Если ключ К с равной вероятностью может прини­мать любое из заданных значений, то в среднем для время .

Поиск по интервалу значений ключа . Алгоритм поиска заключается в последовательном просмотре всех записей файла (т. е. и всех блоков), так как заранее неизвестно, какие записи удовлетворяют условию Q, а какие не удовлетво­ряют. Требуемое время на поиск

Поиск по множеству значений , где а, принимает значения из множества. Алго­ритм поиска заключается в последовательном просмотре всех записей файла, причем для каждой записи осуществляетсяn проверок по равенству . Требуемое время на поиск

Основным достоинством последовательного поиска данных при последовательной организации файла является простота его реа­лизации.

Бинарный поиск. Записи в файле можно упорядочить, напри­мер, по возрастанию или убыванию значения первичного ключа соответственно:

ф

В этом случае можно построить более эффективные алгоритмы поиска, поскольку после сравнения значения а (условие поиска Q: К=а) со значением ключа i-й записи файла ясно, в какой части файла продолжать поиск.

Методы поиска записей в упорядоченном файле различаются друг от друга стратегией выбора очередной записи из файла для выполнения операций сравнения ключа в соответствии с за­данным условием Q. Метод бинарного поиска основан на делении интервала поиска пополам.

Поиск по равенству К= а. Алгоритм поиска заключается в следующем. Файл считают упорядоченным по возрастанию ключа. Сравнивают значение ключа средней записисо значением а. Если, то поиск удачный и алго­ритм заканчивает свою работу. Если , то для продолжения поиска выбирается средняя запись правой половины файла:

ф

Если , то для продолжения поиска выбирали-» средняя запись левой половины файла:

ф

Процесс деления интервала пополам продолжается до тех пор, пока не будет найдена искомая запись (), либо пока в ин­тервале не останется всего одна запись. Если значение ее ключа не удовлетворяет условию поиска, то поиск неудачный и искомой записи в файле нет.

Бинарный поиск можно выполнять, работая с блоками файла, а не с записями. При считывании блока в оперативную память поиск записи в блоке может быть последовательным. В этом слу­чае в качестве характеристик блока используются граничные зна­чения ключей записей, находящихся в блоке.

Поиск по интервалу значений . Алгоритм поиска следующий. Вначале выполняется бинарный поиск записи, значение ключа которой удовлетво­ряет условию, либо, если такой записи нет в файле, то значение клю­ча которой является наиболее близ­ким к а по условию. Далее по­следовательно читаются записи в блоках файла до тех пор, пока не бу­дет нарушено условие:

Поиск по бинарному дереву. Лю­бой бинарный алгоритм поиска в упорядоченном файле можно предста­вить с помощью соответствующего бинарного дерева. В вершинах дерева проставлены номера записей, подлежащих проверке на соответствие условию поиска Это бинарное дерево можно реализовать в виде самостоятельного файла. При этом операции поиска будут освобождены от необходимости каждый раз вычислять адреса записей (они будут сформированы один раз при начальной загрузке файла и при последующих добавлениях в файл новых записей).

Запись бинарного дерева состоит из поля ключа записи и двух полей для указателей. Один указатель для левого поддерева, другой -для правого поддерева. Листовые записи бинарного дерева содержат указатели: на блоки файла ос­новных записей (файла данных). Для уменьшения количества операций обмена с внешней памятью при выполнении поиска соседние записи в бинарном дереве объединяются в блоки.

Записи бинарного дерева обычно меньше по объему па­мяти записей основного файла так как содержат только одно поле данных (поле ключа) и два служебных поля для хра­нения индексов, то при одинаковых размерах блоков количество записей в блоке бинарного дерева больше, чем в блоке основного файла. Это позволяет еще больше сократить количество обраще­ний к внешней памяти.

Реализация бинарного дерева позволяет сократить время по­иска данных по сравнению с бинарным поиском, однако возрас­тает требуемый объем внешней памяти.

Неплотный индекс. Пусть основной файл F упорядочен по полю ключа К. Построим дополнительный файл FD по правилу:

1. записи файла РС имеют формат FD (К, Р), где K-поле, принимающее значение ключа первой записи блока основного файла F, P-указатель на этот блок; 2) записи файла FD упо­рядочены по полю К.

Полученный файл FD называется неплотным индексом . Количество записей файла FD равно количеству блоков основного файла F. Для организации файла FD требуется дополнительная внешняя память.

Поиск вначале выполняется в индексе для нахождения адреса блока основного файла, а затем этот блок считывается в опера­тивную память и в нем, например, с помощью последовательного поиска, определяется требуемая запись.

В -дерево. Так как неплотный индекс упорядочен по клю­чевому полю, то над ним можно построить еще один неплотный индекс (неплотный индекс неплотного индекса) и т. д., пока на самом последнем, верхнем уровне не останется всего один блок. Полученная структура называется В -деревом порядка m, где m-количество записей в блоке индекса. Такое дерево должно иметь в каждом узле не менее m/2 зависимых узлов и все листья должны располагаться на одном уровне.

Для осуществления последовательного поиска блоки первого уровня могут быть связаны в цепь по возрастанию значения ключа. Поиск в В- дереве выполняется так же, как и в неплотном индексе. Удачный и неудачный поиск записи в В -дереве требует h-обменов, где h - число уровней В -дерева.

При поиске по интервалу значений вначале выпол­няется поиск по К.=а в В -дереве, а затем -последовательный поиск по условию в блоках 1-го уровня В -дерева.

Плотный индекс. Пусть по каким-либо причинам невоз­можно упорядочить основной файл F по ключу К. Построим дополнительный файл FD по правилу: 1) записи файла FD имеют формат FD(К, Р), где K -поле, принимающее зна­чение ключа записи основно­го файла; P - указатель на эту запись; 2) записи файла FD упорядочены по полю К.

Полученный файл назы­вается плотным индексом. Он строится почти так же, как и неплотный индекс. Различие заключается в том, что для каждого значения ключа К. в файле FD имеется отдельная запись, а в неплотном индек­се -только для значения клю­ча первой записи блока. Над плотным индексом также можно построить В -дерево.

Перемешанный файл. Размещение и поиск записей в файле выполняется с использованием хеш-адресации. Равномерность рас­пределения записей по блокам файла зависит от равномерности значений ключей в записях файла, от свойств хеш-функции и схемы разрешения коллизий.

При организации хешированного файла во внешней памяти выделяется две области: основная и область переполнения.

Перемешанная организация файла очень эффективна при поиске записей по отдельному значению ключа, однако не позво­ляет производить поиск по интервалу значений ключа.

Поиск по вторичным ключам. Вторичные ключи записи -это любые ее поля, по значениям которых требуется выполнить поиск записей в файле. Поиск по нескольким вторичным ключам называют многоаспектным или многоключевым поиском. Многоаспектный поиск представляет собой сложную проблему.

К настоящему времени разработаны методы поиска ответ;) лишь на конъюнктивные запросы вида

по файлу со схемой записи

Последовательный поиск. Для выполнения многоаспектного поиска можно применять последовательный поиск. В этом случае записи файла перебираются последовательно и проверяются на удовлетворение условию поиска.

Достоинство метода-просто­та, а недостаток - низкая эффек­тивность поиска для запросов, требующих просмотра только ча­сти файла, и которая тем ниже, чем меньшая часть записей фай­ла подлежит выборке.

Инвертированный файл. Ши­роко распространены на практи­ке методы многоаспектного пои­ска по инвертированным файлам. Пусть имеется основной файл F, упорядоченный либо не упорядо­ченный по значениям вторичного ключа . Построим дополни­тельный файлпо правилу: 1) записи файлаимеют формат, где-по­ле, принимающее значение вторичного ключазаписи основного файла;P-указатели на за­писи основного файла F, имеющие данное значение вторичного ключа , 2) записи файла, упорядочены по полю.

Построенный дополнительный файл называется инвертиро­ванным. В этом случае об основном файлеF говорят, что он ин­вертирован по полю . Количество записей в инвертированном файлеопределяется количеством значений вторичного ключав записях основного файлаF.

Рассмотренный способ организации инвертированного файла предполагает использование записей переменной длины. Инвер­тированный файл можно организовать и с помощью записей фик­сированной длины, если в каждой записи инвертированного файла выделять фиксированное число полей для указателей Р. Если фиксированного числа полей для некоторых записей окажется недостаточно, то организуется еще дополнительный служебный файл для хранения неуместившихся цепочек указателей.

Поскольку записи инвертированного файла упорядочены, но значению ключа , то для поиска записей можно использовать любой из рассмотренных выше методов поиска в упорядоченном файле (например, бинарный поиск или В -дерево). Чтобы выпол­нить многоаспектный поиск поn ключам, необходимо построить n инвертированных файлов.