Федеральное государственное бюджетное образовательное учреждения высшего профессионального образования Калининградский государственный технический университет

Кафедра автоматизированного машиностроения

Методические указание

к практической работе №7 по дисциплине «Методы научных исследований» Вычисление выборочных характеристик. Числовые характеристики выборки.

Для студентов очного и запоночного обучения направления 150700.62 «Машиностроение». Методические указание разработал к.т.н., доцент кафедры автоматизированного машиностроения Александров Ю.П.

Методические указания утверждены кафедрой автоматизированного машиностроения

Протокол №___________ от «___» __________ 20____г

Калининград 2013

Оглавление

Цель и задачи работы 3

1Порядок выполнения работы 3

2Структура отчета по работе 6

10

Приложение А. Варианты индивидуального задания по теме «Вычисление выборочных характеристик. Числовые характеристики выборки»………………………………………………………….………………….9

Цель и задачи работы

Цель работы: определить характеристики эмпирического и теоретического распределения частот.

Задачи работы:

1 Освоить методику вычисления числовых характеристик заданной выборки полученных размеров при обработке партии деталей типа «вал». 2 Построить гистограмму и полигон эмпирического и теоритического распределения частот по интервалам полученных размеров. 3 Провести проверку гипотезы о нормальном распределении размеров вала в заданной выборке по критерию Хи-квадрат χ² .

1. Порядок выполнения работы

1 По заданному варианту работы выписать разброс размеров, полученных при обработке партии деталей типа «вал» на токарно-винторезном станке типа 16К20.

Вся совокупность размеров называется выборкой.

2 Отыскать максимальное X_max и минимальное X_min значения выборки. Найти размах или зону рассеяния результатов измерений как разность между наибольшим и наименьшим значениями:

W = X_max – X_min (1)

Построить вариационный ряд массива выборочных значений в порядке возрастания.

3 Определить число интервалов при объёме выборки N ≤ 100 по формуле:

h = 1+3,322lgN, (2)

где N – количество деталей в выборке.

Округлить до целого числа.

4 Определить ширину интервала α, как отношение размаха к числу интервалов:

(3)

5 Подсчитать число n_j выборочных значений, которые попали в j-й интервал, называемое частотой.

6 Каждый интервал представить границами (от и до) и срединным значением и определить относительную частоту попадания размера в j-й интервал. Все полученные исходные данные свести в таблицу 1.

Таблица 1 – Исходные данные для построения гистограммы и полигона распределения частот по интервалам

№ Интервала	Границы интервалов		Срединное значение j-го интервала j	Частота nj	Относительная частота nj / n	Плотность частоты nj /h
	от	до

7 По данным табл. 1 построить гистограмму т.е. график функции n_j=f(j) (см. рис. 1) и полигон распределения частот по интервалам (см. рис. 2)

Рис 2- Полигон частот 1-эмпирическое распределение 2-теоретическое распределение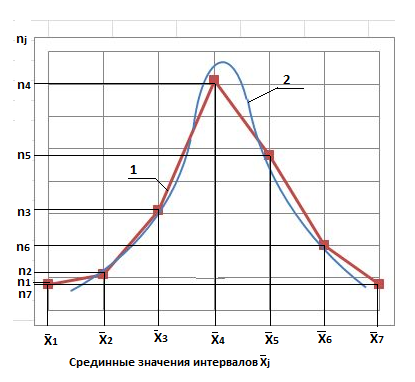

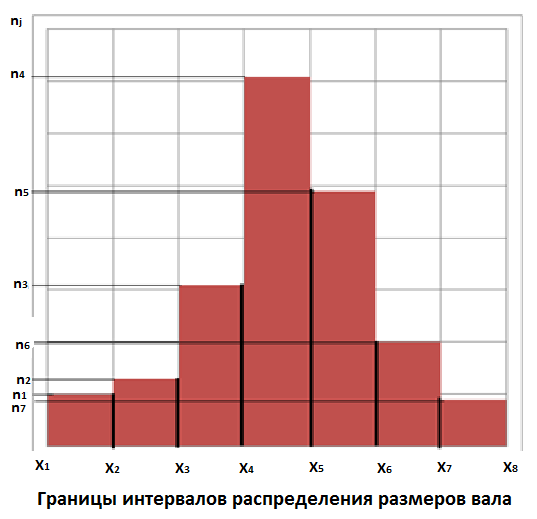
Рис 1- Гистограмма распределения частот

Рис 2-Полигон частот 1-эмпирическое распределение 2-теоретическое распределение

Полигоном частот называют ломанную линию, отрезки которой соединяют точки (₁, n₁), (₂, n₂).... …… (_j, n_j). Для построения полигона частот на оси абсцисс откладывают срединные значения интервалов j, а на оси ординат- соответствующие им частоты n_j. Точки (j, n_j) соединяют отрезками прямых и получают полигон частот. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются ширина интервалов длиною , а высоты равны частотам размеров в каждом j-ом интервале. Для построения гистограммы частот на оси абсцисс откладывают границы интервалов распределения размеров валов. 8 Провести выравнивание эмпирического распределения по нормальному закону и проверку гипотезы о нормальном распределении размеров валов в заданной выборке по критерию согласия Пирсона т. е. по критерию Хи-квадрат –χ². Проверка гипотезы проводится путём сравнения эмпирических частот с теоретическими частотами. Критерий Пирсона позволяет установить на принятом уровне значимости согласие или несогласие эмпирической кривой по нормальному закону распределения. Теоретическую частоту (n_j) в каждом интервале определяем по формуле:

, (4)

где N- объем выборки (количество измерений валов); α- ширина интервала;

f(xj)- функция нормированного отклонения в j-ом интервале, находится по таблице 5 ;

σ - среднее квадратическое отклонение, сигма.

Среднее квадратическое отклонение определяется по формуле:

, (5)

, (6)

где nj - эмпирическая частота в j-ом интервале;

n - сумма эмпирических частот (объем измерений N);

– срединное значение интервала; j- порядковый номер интервала;

Нормированное отклонение средин интервалов x_j находится по формуле:

(7)

где , (8)

Данные для выравнивания эмпирического распределения частот по нормальному закону свести в табл. 3.

9 Определить расчётные значения критерия Пирсона- критерия χ² («Хи-квадрат») в каждом j-ом интервале по формуле:

(9)

где h- число интервалов; n_j- эмпирическая частота в j-ом интервале; _{j –} теоритическая частота в j-ом интервале, определяется по формуле 4.

Число степенной свободы (ⱴ) определяется по формуле:

ⱴ = h-3 (10)

Примечание. Крайние интервалы размеров валов с теоретической частотой n_j < n_min объединяется с соседними интервалами (см. табл. 2) .

Таблица 2- Минимальные значения теоретических частот _min в зависимости от числа степеней свободы

Число степеней свободы ⱴ	1	2	3 ÷ 6	>6
Минимальное значение теоретической частоты min	4	2	1	0,5

После проверки согласно примечания число степеней свободы уточняется с учётом возможного сокращения числа интервалов по формуле 10.

Полученные расчётные значения критерия χ² («Хи-квадрат») по формуле 9сравниваются с табличным значением критерия χ₃² при 5-ти процентном уровне значимости. (см. табл. 6) для окончательно определенного числа степеней свободы. Для оценки различия эмпирического распределения частот от теоретического по критерию χ² («Хи-квадрат») все выполненные расчёты свести в табл.4.

Если расчётное значение критерия χ_р² меньше табличного значения χ_табл², то различие эмпирического распределения частот от теоретического не достоверно. Эмпирическое распределения можно считать нормальным.