Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Калининградский государственный технический университет

Кафедра автоматизированного машиностроения

Методические указания

к практической работе №6

по дисциплине “Методы научных исследований”

Оценка погрешности экспериментального определения физической величины

Для студентов очного и заочного обучения направления 150700.62

“Машиностроение”

Методические указания разработал к.т.н.,

доцент кафедры автоматизированного машиностроения

Александров Ю.П

Методические указания утверждены на заседаний кафедры автоматизированного машиностроения

Протокол № от_

Калининград

2013

Содержание

Введение……………………………………………………………………...3

1 Цель и задачи работы………………………………………………………4

2 Структура отчёта по работе………………………………………………..8

Список использованных источников………………………………………..9

Приложение А. Варианты индивидуального задания по теме практической работы “Оценка погрешности экспериментального определения физической величины”...............................................................................................10

Введение

Методика обработки прямых измерений изложена в работах [1,2,3].

Наилучшей оценкой истинного значения величины Х является выборочное среднее значение

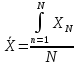, (1)

где 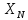- отчёт величины Х;

N- число отчётов;

n- порядковый номер измерения физической величины.

Для оценки разброса отсчётов при измерении используется выборочное среднее квадратическое отклонение отсчётов

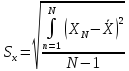(2)

Выборочное среднее является случайной величиной и его разброс относительного истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения

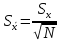(3)

Доверительным интервалом называется интервал [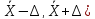, который с заданной степенью достоверности включает в себя истинное значения измеряемой величины. В выражение [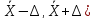входят: выборочное среднее значение 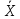и полная погрешность многократных измерений ∆.

Доверительной вероятностью (надёжностью) результата серии наблюдений называется вероятность а, с которой доверительный интервал включает истинное значение измеряемой величины.

Случайную составляющую погрешность принято выражать как полуширину доверительного интервала.

Размер доверительного интервала обычно задают в виде кратного 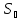значения.

Тогда случайная составляющая погрешности многократных измерений определяется как:

∆Х= 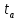*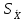, (4)

где 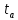– безразмерный коэффициент доверия ( коэффициентCтьюдента).

Коэффициент 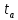показывает, во сколько раз нужно увеличить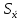, чтобы при заданном числе измерений получить заданную надёжность их результата.

Коэффициент 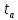определяют по таблице 1.

Полная погрешность ∆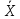прямых измерений равна квадратичной сумме её составляющих: инструментальной 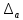и случайной.

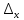Обработку прямых измерений рекомендуется начинать с проверки отчётов на наличие промахов. Из полученного ряда, содержащего N отсчётов, выбирается аномальный отсчёт 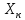и вычисляется модуль его отклонения от среднего значения в долях выборочного среднего квадратического отклонения:

Z=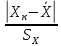(5)

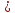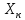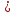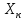Затем вычисляется вероятность этого отклонения, а также ожидаемое число n измерений, которые дадут отсчёты, имеющие отклонение Z не меньше, чем испытуемый. Если получено n 0,5 (при округлении до целого n=0), то отсчёт считается промахом. Эту процедуру можно изменить и вычислить ожидаемое числоM отсчётов, среди которых будет хотя бы один аномальный. Если MN, то отсчёт считается промахом. Связь междуM и Z приведена в таблице 2.