Анал_Геом / Транспонирование матрицы

Транспонирование матрицы

Над матрицами определена еще одна операция, называемая транспонированием.

        Определение 14.5   Пусть -- матрица размеров . Тогда транспонированной матрицей называется такая матрица размеров , что , , .         

Транспонированная матрица обозначается или . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

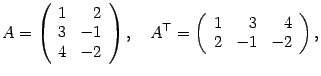
Читатель легко проверит, что

где -- число.

        Предложение 14.5   Если произведение определено, то

(14.8)

        Доказательство.     Пусть -- матрица размеров ,  -- матрица размеров . Тогда имеет размеры ,  -- размеры . Число столбцов в совпадает с числом строк в , поэтому произведение на определено. Размеры этого произведения . Матрица имеет размеры , поэтому  -- матрица размеров . Итак, матрицы в правой и левой части равенства (14.8) существуют и имеют одинаковые размеры.

Пусть , , , , . Нам нужно показать, что , , .

По определению транспонирования . По определению умножения матриц

(14.9)

С другой стороны,

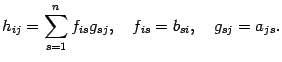
Поэтому

Сравнивая полученный результат с (14.9), получаем .