Анал_Геом / Матрица и действия над ними

Матрица и действия над ними

Матрица – размером m на n, называется прямоугольная таблица, состоящая из m n чисел расположенных в m строках и n столбцах.

Квадратная матрица – m=n

Диагональная матрица – все не диагональные элементы равны 0

Скалярная матрица – все диагональные элементы равны между собой.

Согласованная матрица с другой матрицей – когда чисто столбцов первой матрицы = чисту строк второй.

Комутативная или перестановочная матрица - AB = BA

Транспонирование – замена строк на столбцы

Перестановки и подстановки

Число перестановок – n! (число элементов)

Инверсией в перестановке называется такое расположение ее элементов, при котором элемент с большим порядквым номером предшествует элементу с меньшим.

Перестановка называется четной(нечетной), если общее чисто инверсий образуемых ее элементыми четно(нечетно) n!/2

Транспозиция – Преобразование перестановки, при котором меняются местами какие-либо два ее элемента.

Подстановка n-го порядка(степени) – взаимно однозначное отображение множества n-первых натуральных чисел на себя

Подстановка называется четной(нечетной), если количество инверсий во второй строке ее канонической формы (вида) четна (нечетна)

Определители n-го порядка. Свойства

Определитель n-го порядка кв. м. – алгебраическая сумма n! слагаемых.

Детерминантным отображением множества – когда каждой матрице ставится в соответствие число.

Свойства:

1. При транспонировании матрицы ее определитель не изменяется.

2. Если в определителе содержится одна 0-я строка, то определитель равен 0.

3. Если в определителе поменять две строки местами, то его значение поменяется на противоположное.

4. Определитель, содержащий две одинаковые строки будет равен 0

5. Общий множитель какой-либо строки можно вынести за знак определителя.

6. Определитель, содержащий две пропорциональные строки равен 0

7. Если элементы i-й строки представить в виде суммы 2-х слагаемых, то такой определитель равенн сумме двух определителей.

8. Если обна из строк определителя является линейной комбинацией других его строй, то такой определитель равен 0.

9. Определитель не измениться, если к элементам одной из его строк прибавить соответствующие элементы другой строки, умноженные на некоторое число.

Разложение определителя по элементам строки.

Минором элемента определителя n-го порядка – определитель n-1 порядка, полученный из данного, вычеркиванием i-й строки и j-го столбца.

Алгебраическое дополнение – минор этого элемента, взятый со знаком (-1)^i+j

Теорема: если все элементы i-й строки (столбца) определителя D, кроме 1-го равны 0, то определитель D равен произведению элементов на его алгебраическое дополнение.

…

Теорема: определитель равен сумме произведений элементов какой-либо строки на их алгебраическое дополнение.

…

Теорема Лаппласа: Пусть в определителе D порядка n произвольно выбраны k строк (столбцов), где , тогда сумма произведений всех миноров k-го порядка, содержащегося в выбранных строках, на их алгебраическое дополнение равна определителю D

Правило Крамера.

Если определитель системы и линейной системы с неизвестным отличен от 0, то система имеет единственное решение, которое находится по формуле

Обратная матрица. Матричные уравнения.

Обратной матрицей по отношению к А – матрица А^-1, что А А^-1= А^-1 А=Е

Квадратная матрица называется невырожденной –

Квадратная матрица называется вырожденной –

Свойства:

(A^-1) ^-1=A (AB) ^-1=B^-1A^-1

1. AX=B; А^-1AX= А^-1B; EX= А^-1B; X= А^-1B

2. XA=B; XA А^-1=B А^-1; X=B А^-1;

3. AXB=C; А^-1AXBB^-1= А^-1C B^-1; X= A^-1C B^-1

Метод Гаусса решения систем линейных уравнений.

Метод исключения переменных. Привод системы к ступенчатому виду, получим k-уравнений. k=n – треугольный вид. k<n – трапецевидный вид. k>n – недоконца преобразовано

Совместная система – если система уравнений имеет хотя бы одно решение.

Несовместная система – если система уравнений не имеет хотя ни одно решения.

Определенная система – если есть одно решение.

Неопределенная система – если более одного решения.

Теорема: Произвольную невырожденную м.А с помощью элементарных преобразований можно привести к единичной.

Теорема: Если к единичной м. порядка n применить теже элементарные преобразования только над строками и в том же порядке, с помощью которых невырожденная м. А порядка n приводится к единичной, то полученная м. M будет обратной м. A

Понятие вектора. Линейные операции над вектором.

Скаляр – величина, характеризующиеся количественным значением, задается действительным числом.

Вектор – величина, характеризующаяся не только количественным значением, но и направлением.

Геометрический вектор (направленный отрезок) – пара точек, соединенных между собой, начало и конец.

Модуль или Длина – длина отрезка, соединяющая его начало и конец.

Ортом – называется , направление которого совпадает с направлением

Колинеарные вектора – вектора, лежащие на одной прямой, или на ||

Компланарные вектора – вектора, лежащие в одной плоскости.

Пр_i=||

Линейная зависимость векторов. Свойства линейно зависимых векторов.

Выражение вида , где , называется Лиенйной комбинацией векторов .

Базис на прямой – любой этой прямой

Базис на плоскости – 2 неколинеарных вектора на этой плоскости, взятые в определенном порядке.

Базис в пространстве – 3 некомпланарных вектора, взятые в определенном порядке.

Теорема:

Каждый вектор || какой-либо прямой(плоскости)(3D), может быть разложен по базису на этой прямой(плоскости)(3D).

Тривиальная линейная комбинация – если все ее коэфф = 0

Нетривиальная линейная комбинация – если хотябы один ее коэфф 0

Линейно зависимые вектора - , если нетривиальная линейная комбинация этих векторов = .

Линейно независимые вектора – если только тривиальная линейная комбинация =0

Свойства линейно зависимых векторов:

1. Для того, чтобы были линейно зависимы, Н и Д, чтобы хотябы один из них являлся линейной комбинацией остальных.

2. Если среди n-векторов есть , то вся система линейно независима.

3. Если подсистема данной системы векторов линейно зависима, то и вся система линейно зависима.

4. Если вся система векторов линейно независима, то и любая ее подсистема незасисима.

Система координат.

Д.с.к. в пространстве - совокупность точки и базиса.

Орто нормированный базис – если его вектора попарно ортонормированы и имеют единичную длину.

П.с.к. – считается определена, если на плоскости задана некоторая точка О(полюс), и исходящей из нее луч(полярная ось).

Связ:

Деление отрезка в заданном отношении.

Скалярное произведение векторов.

С.п.в. -

Угол между векторами – угол, между равными им векторами, и имеющими общее начало.

Свойства:

1. Коммутативно

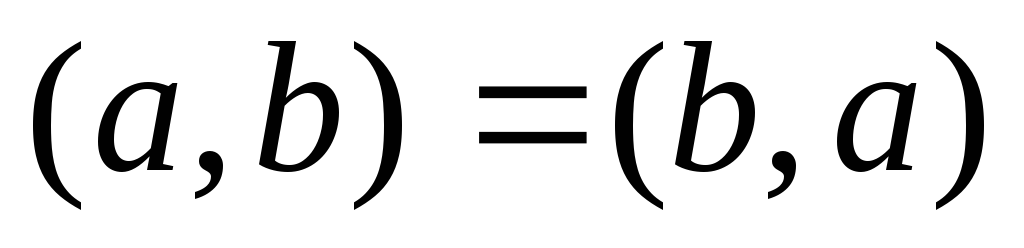
2. Множитель можно выносить за скобки

3. (,)=||²

4. Если , то (,)=0

5. (,)=|| орт.пр_ab

6. Дистрибудивность

Теорема: скалярное произведение 2-х векторов, заданных ортонормированном базисе = сумме произведений их соответствующих координат.

Проекция векторов на ось.

Векторное произведение векторов.

В.п.в. - , удовлетворяющий следующим условиям.

1. || = ||=||||

2.

3. {,,} образуют правую ориентацию

Свойства:

1. || численно равен S параллелограмма, построенного на этих векторах

2. В.п. антикоммутативно = -

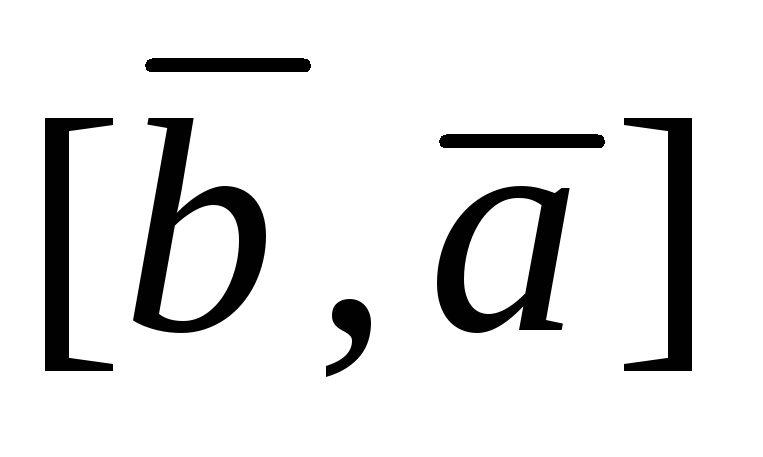
3. Скалярный множитель можно выносить

4. Закон дистрибутивности

Теорема: Если и заданы своими координатами, относительно ортонормированного базиса, то =

Некоторые приложение скалярного и векторного произведения.

1. Работа постоянной силы

2. Пр вектора на заданное направление

3. Момент силы относительно точки

4. Нахождение S параллилепипеда и

5. Нахождение линейной скорости вращения

Смешанное произведение трех векторов.

С.п.3.в. – называется произведение , на и (,])

Теорема: с.м.3.в, заданных в своих координатах в ортонормированном базисе, есть определитель 3-го порядка, составленных из координат данных векторов.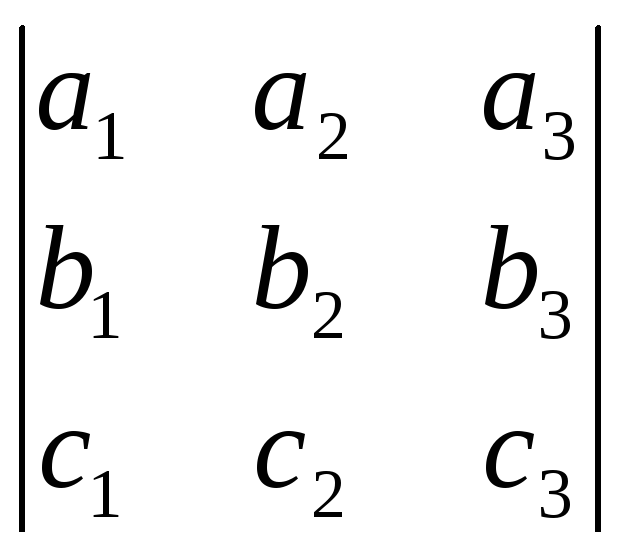

Свойства:

1.Скобки можно переставлять

2.Для того, чтобы векторы были компланарны, Н и Д, чтобы определитель 3-го порядка, составленный из их координат, был равен нулю.

3.С.п.3.в. = V параллилепипеда, построенного на этих векторах

Формула преобразования координат на плоскости.

Стр 40

Понятие линии на плоскости. Различные способы задания прямой на плоскости.

Линия – множество всех точек плоскости, координаты которых удовлетворяют уравнению f(x,y)=0.

Способы:

1. Задание прямой начальной точкой и направляющим вектором

2. Уравнение прямой, проходящей через две точки

3. Уравнение прямой в отрезках

4. Задание прямой по начальной точке и угловому коэффициенту.

5. Параметрическое уравнение прямой

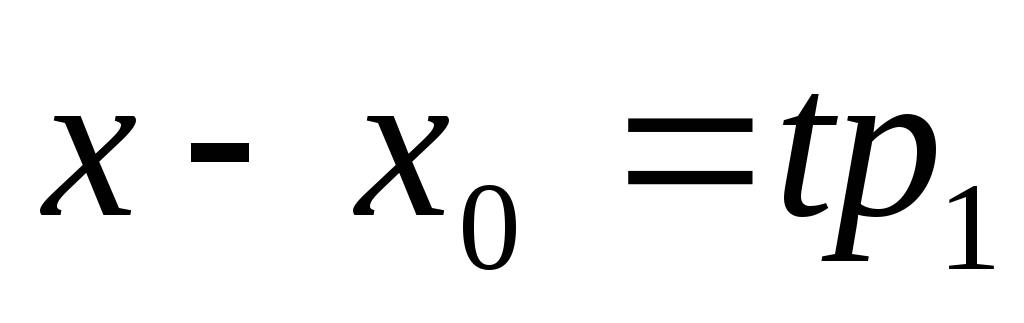
6. Уравнение прямой линии, проходящей через данныую точку, данному вектору.

7. Общее уравнение прямой

8. Полярное уравнение прямой

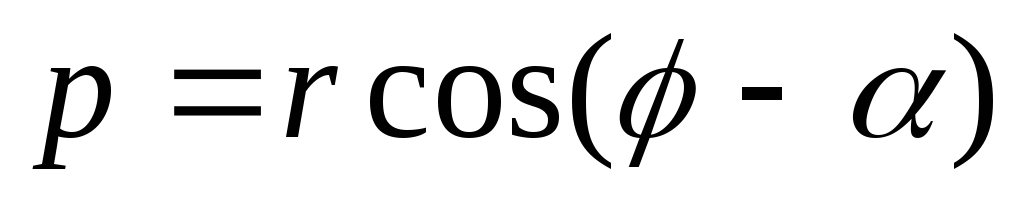
9. Нормальное уравнение прямой

Расстояние от точки до прямой на плоскости. Угол между двумя прямыми

Стр 48

Пучок прямых на плоскости.

Стр 49-50

Пучок прямых – Совокупность всех прямых, лежащих в данной плоскости и проходящих черех фиксированную точку.

Различные способы задания плоскости в пространстве.

1. Задание плоскости относительно прямоугольной д.с.к. точкой и вектором нормалей.

2. По точке и 2-м некомпланарным направляющимввекторам.

3. По 3-м точкам не лежащих на одной прямой.

4. Параметрическое уравнение плоскости

5. Задание плоскости в отрезках

Различные способы задания прямой в пространстве.

1. Направляющий вектор прямой

2. Задание прямой по точке и направляющему вектору

3. По 2-м точкам

4. Параметрическое уравнение прямой

Расстояние от точки до прямой и плоскости в пространстве.

Расстояние между скрещивающимися прямыми. Угол между прямой и плоскостью.

Уравнение окружности.

Эллипс.

Пусть на плоскости заданы фиксированные точки F₁ и F₂, расстояние между которыми равно 2C (F₁ F₂=2С)

Множество всех точек плоскости, сумма расстояний которой до двух фиксированных точек F₁ и F₂ называется фокусами = 2а

Гипербола.

Г – геометрическое место точек плоскости, модуль разности расстояний которых от 2-х фиксированных точек F₁ и F₂ плоскости есть постоянное число, меньшее, чем расстояние между F₁ и F_2.

Парабола.

П – геометрическое место точек плоскости, для которых расстояние от некоторой фиксированной точки F плоскости равно расстоянию до некоторой фиксированной прямой d, не проходящей через точку .

Уравнение линии 2-го порядка в полярноых координатах.

Классификация кривых 2-го порядка.

Эллипс

Гипербола

Парабола

Мнимый эллипс

Уравнение 2-х прямых

Пара комплексных прямых

Пара параллельных действительных прямых

Пара мнимых параллельных прямых

Здвоинная прямая