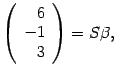Анал_Геом / Изменение координат вектора при изменении базиса

Изменение координат вектора при изменении базиса

Пусть в -мерном линейном пространстве выбран базис , который мы будем для удобства называть "старый" и другой базис , который мы будем называть "новый". Возьмем призвольный вектор из . Его координатный столбец в старом базисе обозначим , а в новом -- . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.

        Замечание 18.1   Матрица перехода всегда невырождена, то есть .         

        Предложение 18.5   Координатные столбцы в старом базисе и в новом базисе связаны формулой

(18.1)

где справа стоит произведение матрицы перехода на матрицу-столбец.

        Доказательство.     Так как  -- координатный столбец вектора в новом базисе, то

Заменив векторы их разложениями по старому базису, получим

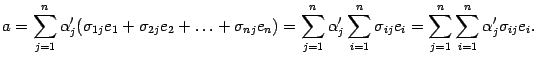
В силу предложения 14.3 изменим порядок суммирования

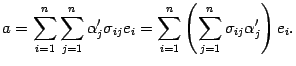
Здесь мы получили разложение вектора по старому базису, причем координата вектора с номером равна . Элемент с номером столбца будет иметь такой же вид. Следовательно, формула  (18.1) доказана.     

        Пример 18.4   Пусть , то есть  -- трехмерное векторное пространство. Пусть задан ортонормированный базис i, j, k. Выберем другой (новый) базис

Возьмем вектор . Найдем его координаты в новом базисе.

Выпишем матрицу перехода, ее столбцы -- это координаты новых базисных векторов

Пусть 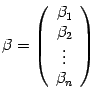 -- координатный столбец вектора в новом базисе. Тогда

(18.2)

откуда

Найдем матрицу по формуле (14.14). Находим определитель

Находим алгебраические дополнения

Следовательно,

Находим координаты вектора

Таким образом, новые координаты вектора : , , , .

Тот же самый результат можно было получить, записав формулу (18.2) в виде системы уравнений

Решив эту систему, например, методом Гаусса, найдем новые координаты , , .