Анал_Геом / Базис и размерность пространства

Базис и размерность пространства

Так как в линейном пространстве векторы можно складывать и умножать на числа, то из них можно составлять линейные комбинации и можно ввести понятия линейной зависимости и линейной независимости системы векторов так же, как это было сделано в разделе "Линейная зависимость векторов". На случай произвольного линейного пространства определения 10.14 и 10.15 переносятся дословно. Предложения 10.6, 10.7, 10.8 переносятся дословно вместе с доказательствами.

На основе линейной зависимости в линейном пространстве вводится определение базиса. Оно почти дословно совпадает с определением 10.16.

        Определение 18.2   Базисом линейного пространства называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства является линейной комбинацией этих векторов.         

В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

        Пример 18.2   Пусть -- линейное пространство всех многочленов с веществеными коэффициентами. Покажем, что в этом пространстве базис не существует.

Предположим противное. Пусть векторы образуют в этом пространстве базис.

Каждый вектор пространства  -- это многочлен. Пусть

Из степеней многочленов выберем наибольшую и обозначим ее буквой . Возьмем многочлен . Так как и векторы образуют базис, то , где  -- вещественные числа. Следовательно, является суммой многочленов степеней меньших, чем , и поэтому его степень должна быть меньше, чем . С другой стороны, по определению, многочлен имеет степень . Получили противоречие. Значит, предположение о существовании базиса неверно.         

        Теорема 18.1   В линейном пространстве любые два базиса содержат одинаковое число векторов.     

Доказательство теоремы мы приводить не будем. Желающие могут найти его в любом учебнике по линейной алгебре, например в [1].

        Определение 18.3   Линейное пространство , в котором существует базис, состоящий из векторов, называется -мерным линейным или векторным пространством. Число называется размерностью пространства и обозначается . Линейное пространство, в котором не существует базис, называется бесконечномерным.         

Примером бесконечномерного пространства является пространство всех многочленов с вещественными коэффициентами. Как показано в  примере 18.2 в этом пространстве базис отсутствует.

        Предложение 18.1   Пространство столбцов из элементов, являющихся вещественными числами, имеет рамерность .

        Доказательство.     Возьмем систему векторов

Покажем, что эта система линейно независима. Составим линейную комбинацию и приравняем ее к нулю:

Преобразуем левую часть:

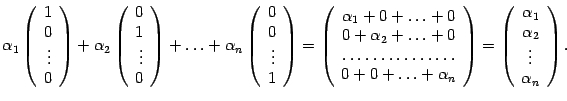
Следовательно,

откуда , , . Итак, система векторов  -- линейно независима.

Пусть -- произвольный вектор пространства, Очевидно, что

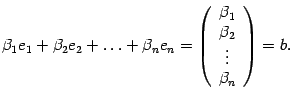
Следовательно, вектор является линейной комбинацией векторов . Тем самым доказано, что векторы образуют базис в пространстве столбцов из элементов. Размерность пространства равна числу векторов в базисе. Следовательно, пространство -- -мерное.     

Пространство столбцов из элементов, являющихся вещественными числами, обозначается .

        Предложение 18.2   Пространство столбцов из элементов, являющихся комплексными числами, имеет размерность .     

Доказательство такое же, как и в предыдущем предложении. Это пространство обозначается .

        Пример 18.3   Пространство решений однородной системы линейных уравнений имеет базис из решений, где  -- число неизвестных, а  -- ранг матрицы . Этим базисом служит фундаментальная система решений (см.  определение 15.5 и  теорему 15.3).