
Анал_Геом / Приведение уравнения второго порядка к каноническому виду
.docПриведение уравнения второго порядка к каноническому виду
В главе "Поверхности второго порядка", где рассматривались поверхности второго порядка, было выписано их общее уравнение (13.1), а дальше для каждой поверхности использовалась своя прямоугольная декартова система координат, в которой уравнение поверхности имело канонический вид. В этом разделе мы выясним, как по общему уравнению найти такую систему координат. Результаты этого раздела используются и для приведения общего уравнения кривой второго порядка к каноническому виду. Достаточно будет во всех рассуждениях отбросить третью координату.
Пусть в пространстве задана прямоугольная
декартова система координат
![]() .
Рассмотрим общее уравнение поверхности
второго порядка, коэффициенты в котором
обозначены специальным образом
.
Рассмотрим общее уравнение поверхности
второго порядка, коэффициенты в котором
обозначены специальным образом
|
|
(19.7) |
где
![]() --
числа, причем хотя бы одно из чисел
--
числа, причем хотя бы одно из чисел
![]() отлично
от нуля.
отлично
от нуля.
Выделим квадратичную часть выражения, стоящего в уравнении слева,
![]()
Такое выражение называется квадратичной формой от трех переменных. Составим матрицу

Эта матрица называется матрицей
квадратичной формы
![]() .
Она является симметричной, то есть
.
Она является симметричной, то есть
![]() ,
или, другими словами,
,
или, другими словами,
![]() .
Следует обратить внимание на то, как
эта матрица составлена. На диагонали у
нее стоят коэффициенты при квадратах
переменных, а в остальных местах --
половины коэффициентов при произведениях
переменных.
.
Следует обратить внимание на то, как
эта матрица составлена. На диагонали у
нее стоят коэффициенты при квадратах
переменных, а в остальных местах --
половины коэффициентов при произведениях
переменных.
Исходная система координат является
прямоугольной, поэтому скалярное
произведение векторов с координатными
столбцами
 ,
,
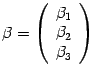 задается
формулой
задается
формулой
![]() .
Сформулируем две теоремы, позволяющие
пользоваться приведенным ниже алгоритмом.
.
Сформулируем две теоремы, позволяющие
пользоваться приведенным ниже алгоритмом.
Теорема
19.4 Если матрица
![]() --
симметричная, то ее собственные числа
являются вещественными числами и
существует ортонормированный базис из
собственных векторов.
--
симметричная, то ее собственные числа
являются вещественными числами и
существует ортонормированный базис из
собственных векторов.
Пусть
![]() --
матрица квадратичной формы
--
матрица квадратичной формы
![]() .
По сформулированной теореме у нее
существует ортонормированный базис из
собственных векторов. Обозначим их
.
По сформулированной теореме у нее
существует ортонормированный базис из
собственных векторов. Обозначим их
![]() ,
,
![]() ,
,
![]() ,
и пусть эти векторы имеют координаты
,
и пусть эти векторы имеют координаты

Базис i, j, k назовем старым,
а базис
![]() --
новым. Тогда матрица перехода 19.1.4.а
будет иметь вид
--
новым. Тогда матрица перехода 19.1.4.а
будет иметь вид

Выберем новую систему координат
![]() так,
что начало координат не изменяется, а
новые базисные векторы
так,
что начало координат не изменяется, а
новые базисные векторы
![]() ,
,
![]() ,
,
![]() задают
направления новых координатных осей
задают
направления новых координатных осей
![]() ,
,
![]() ,
,
![]() (рис.
19.8).
(рис.
19.8).

Рис.19.8.Система
координат
![]()
Тогда координаты
![]() точки
точки
![]() являются
координатами ее радиус-вектора
являются
координатами ее радиус-вектора
![]() и,
следовательно, при замене базиса меняются
по формуле (18.1)
и,
следовательно, при замене базиса меняются
по формуле (18.1)
|
|
(19.8) |
Теорема
19.5 Пусть собственные
векторы
![]() ,
,
![]() ,
,
![]() матрицы
квадратичной формы
матрицы
квадратичной формы
![]() ,
образующие ортонормированный базис,
соответствуют собственным числам
,
образующие ортонормированный базис,
соответствуют собственным числам
![]() ,
,
![]() ,
,
![]() .
Тогда в системе координат
.
Тогда в системе координат
![]() квадратичная
форма принимает вид
квадратичная
форма принимает вид
![]()
Если мы из равенства (19.8)
выпишем выражение
![]() ,
,
![]() ,
,
![]() через
новые переменные
через
новые переменные
![]() ,
,
![]() ,
,
![]() и
подставим в уравнение (19.7),
то обнаружим, что квадратичная его часть
и линейная часть преобразуются независимо
друг от друга. В результате уравнение
в системе координат
и
подставим в уравнение (19.7),
то обнаружим, что квадратичная его часть
и линейная часть преобразуются независимо
друг от друга. В результате уравнение
в системе координат
![]() имеет
вид
имеет
вид
|
|
(19.9) |
Хотя бы одно из чисел
![]() ,
,
![]() ,
,
![]() отлично
от нуля, иначе матрица
отлично
от нуля, иначе матрица
![]() была
бы нулевой.
была
бы нулевой.
Рассмотрим три случая.
-
Пусть все собственные числа
 ,
,
 ,
,
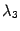 отличны
от нуля. В уравнении (19.9)
выделим полные квадраты
отличны
от нуля. В уравнении (19.9)
выделим полные квадраты
![]()
Выполним параллельный перенос системы
координат
![]() ,
взяв за новое начало системы координат
точку
,
взяв за новое начало системы координат
точку
![]() (см.
формулы (13.21)).
Тогда в новой системе координат
(см.
формулы (13.21)).
Тогда в новой системе координат
![]() уравнение
запишется в виде
уравнение
запишется в виде
![]()
Здесь возможны следующие варианты.
-
Пусть
 .
Перенесем
.
Перенесем
 в
правую часть и поделим обе части на
в
правую часть и поделим обе части на
 ,
получим
,
получим
![]()
-
Если числа
 ,
,
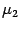 ,
,
 отрицательны,
то ни одна точка пространства не
удовлетворяет этому уравнению. Говорят,
что оно определяет мнимый эллипсоид.
отрицательны,
то ни одна точка пространства не
удовлетворяет этому уравнению. Говорят,
что оно определяет мнимый эллипсоид.
-
Если числа
 ,
,
 ,
,
 положительны,
то уравнение является каноническим
уравнением эллипсоида.
положительны,
то уравнение является каноническим
уравнением эллипсоида.
-
Если одно из чисел
 ,
,
 ,
,
 отрицательно,
а остальные положительны, то (после
переименования осей) получим каноническое
уравнение однополостного гиперболоида.
отрицательно,
а остальные положительны, то (после
переименования осей) получим каноническое
уравнение однополостного гиперболоида.
-
Если одно из чисел
 ,
,
 ,
,
 положительно,
остальные отрицательны, то (после
переименования осей) получим каноническое
уравнение двуполостного гиперболоида.
положительно,
остальные отрицательны, то (после
переименования осей) получим каноническое
уравнение двуполостного гиперболоида.
-
Пусть
 .
.
-
Если все числа
 ,
,
 ,
,
 положительны,
то только начало координат удовлетворяет
этому уравнению. Поверхность выродилась
в точку.
положительны,
то только начало координат удовлетворяет
этому уравнению. Поверхность выродилась
в точку.
-
Если одно из чисел
 ,
,
 ,
,
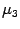 отрицательно,
а два положительны, то (после
переименования осей) получим каноническое
уравнение конуса.
отрицательно,
а два положительны, то (после
переименования осей) получим каноническое
уравнение конуса.
-
Если же два числа отрицательны или все
три отрицательны, то, умножив обе части
уравнения на
![]() ,
получим случай 2
или случай 1.
,
получим случай 2
или случай 1.
-
Пусть одно из чисел
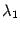 ,
,
 ,
,
 равно
нулю, а два других отличны от нуля.
Допустим, что
равно
нулю, а два других отличны от нуля.
Допустим, что
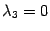 .
Тогда в уравнении (19.9)
выделим полные квадраты по переменным
.
Тогда в уравнении (19.9)
выделим полные квадраты по переменным
 ,
,

![]()
-
Пусть
 .
Преобразуем уравнение к виду
.
Преобразуем уравнение к виду

Поделим обе части уравнения на
![]() и
выполним параллельный перенос осей
координат, взяв за новое начало координат
точку
и
выполним параллельный перенос осей
координат, взяв за новое начало координат
точку
![]() .
Получим уравнение
.
Получим уравнение
![]()
-
Если числа
 и
и
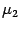 положительны,
то это -- каноническое уравнение
эллиптического параболоида.
положительны,
то это -- каноническое уравнение
эллиптического параболоида.
-
Если
 ,
,
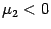 ,
получим каноническое уравнение
гиперболического параболоида.
,
получим каноническое уравнение
гиперболического параболоида.
Если числа
![]() и
и
![]() отрицательны
или
отрицательны
или
![]() ,
,
![]() ,
то сменим направление у оси
,
то сменим направление у оси
![]() на
противоположное и получим либо случай 1,
либо случай 2.
на
противоположное и получим либо случай 1,
либо случай 2.
-
Пусть
 .
Тогда поверхность является цилиндрической,
образующие которой параллельны оси
.
Тогда поверхность является цилиндрической,
образующие которой параллельны оси
 ,
а направляющей служит кривая на
плоскости
,
а направляющей служит кривая на
плоскости
 с
уравнением
с
уравнением
![]()
Анализ поверхностей с таким уравнением предоставляем читателю.
-
Пусть только одно из чисел
 ,
,
 ,
,
 отлично
от нуля. Допустим, что
отлично
от нуля. Допустим, что
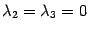 .
Тогда в уравнении (19.9)
выделим полный квадрат по переменному
.
Тогда в уравнении (19.9)
выделим полный квадрат по переменному
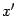
![]()
-
Пусть хотя бы одно из чисел
 ,
,
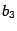 отлично
от нуля. Тогда на плоскости
отлично
от нуля. Тогда на плоскости
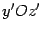 возьмем
две перпендикулярные прямые
возьмем
две перпендикулярные прямые
 и
и
 .
Возьмем новую систему координат, у
которой начало будет в точке
.
Возьмем новую систему координат, у
которой начало будет в точке
 ,
ось
,
ось
 направлена
по оси
направлена
по оси
 ,
ось
,
ось
 направлена
вдоль второй прямой, а ось
направлена
вдоль второй прямой, а ось
 направлена
вдоль первой прямой. Тогда уравнение
примет вид
направлена
вдоль первой прямой. Тогда уравнение
примет вид
![]()
Это -- уравнение цилиндрической
поверхности, образующие которой
параллельны оси
![]() ,
а направляющей служит кривая на плоскости
,
а направляющей служит кривая на плоскости
![]() с
уравнением
с
уравнением
![]()
Анализ возможных поверхностей оставляем читателю.
-
Пусть
 .
Тогда уравнение принимает вид
.
Тогда уравнение принимает вид

-
Если число справа положительно, то уравнение определяет две плоскости

-
Если число справа равно нулю, то уравнение определяет одну плоскость
![]()
-
Если число справа отрицательно, то ни одна точка пространства уравнению не удовлетворяет.
Итак, получен алгоритм, позволяющий установить, какая поверхность задается уравнением второго порядка и каково ее положение в пространстве.
Пример 19.11 Приведите уравнение поверхности
![]()
к каноническому виду.
Решение. Квадратичная форма имеет вид
![]()
Выписываем ее матрицу

Находим ее собственные числа. Для этого запишем характеристическое уравнение

После вычисления определителя получим
![]()
Подбором находим один корень
![]() .
Преобразуем уравнение, выделяя множитель
.
Преобразуем уравнение, выделяя множитель
![]()
![]()
или
![]()
откуда
![]()
Находим два других корня характеристического
уравнения
![]() и
и
![]() .
.
Находим собственные векторы. Для
собственного числа
![]() для
координат собственного вектора
для
координат собственного вектора
![]() получим
систему уравнений
получим
систему уравнений

Решая ее находим, что фундаментальная
система решений содержит только одно
решение, и в качестве собственного
вектора можно взять
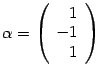 .
Для собственного числа
.
Для собственного числа
![]() для
координат собственного вектора
для
координат собственного вектора
![]() получим
систему уравнений
получим
систему уравнений

Отсюда находим собственный вектор
 .
Для собственного числа
.
Для собственного числа
![]() для
координат собственного вектора
для
координат собственного вектора
![]() получим
систему уравнений
получим
систему уравнений

Отсюда находим собственный вектор
 .
.
Легко проверить, что
![]() ,
то есть собственные векторы попарно
ортогональны. Их длины равны соответственно
,
то есть собственные векторы попарно
ортогональны. Их длины равны соответственно
![]() ,
,
![]() ,
,
![]() .
Поэтому векторы нового ортонормированного
базиса будут иметь координаты
.
Поэтому векторы нового ортонормированного
базиса будут иметь координаты

Матрица перехода имеет вид

Старые координаты связаны с новыми
уравнением
 ,
то есть
,
то есть
|
|
(19.10) |
Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа

Приводим подобные члены

Выделим полные квадраты

или

Выполняем параллельный перенос осей координат

Новое начало системы координат
![]() имеет
координаты
имеет
координаты

В исходной системе координат точка
![]() в
соответствии с формулами (19.10)
имеет координаты
в
соответствии с формулами (19.10)
имеет координаты


Рис.19.9.Система
координат
![]()
В новой системе координат
![]() (рис.
19.9) уравнение принимает канонический
вид
(рис.
19.9) уравнение принимает канонический
вид

Это уравнение является каноническим
уравнением однополостного гиперболоида.
Его центр находится в точке
![]() ,
две вещественные оси параллельны
векторам
,
две вещественные оси параллельны
векторам
![]() ,
,
![]() ,
вещественные полуоси равны
,
вещественные полуоси равны
![]() ,
,
![]() .
Мнимая ось параллельна вектору
.
Мнимая ось параллельна вектору
![]() ,
мнимая полуось равна
,
мнимая полуось равна
![]() .
Изображение гиперболоида приведено на
рисунке 19.10.
.
Изображение гиперболоида приведено на
рисунке 19.10.
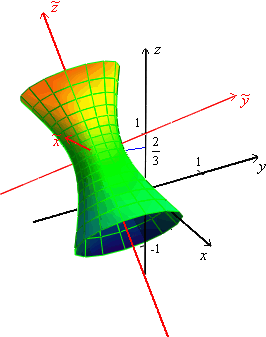
Рис.19.10.Изображение гиперболоида


