Угловая скорость вращения
векторов A1 и A2 одинакова и равна частоте колебаний, поэтому угол
между этими векторами остается неизменным и равным разности фаз 02 – 01 колебаний.
Тогда вектор A = A1 + A2 также вращается вокруг точки O с угловой скоростью , а его длина A
(амплитуда суммарного колебания) равна диагонали параллелограмма, построенного на векторах A1 и A2:
A 
A12 A22 2A1 A2 cos( 02 01 )
Как видно из рисунка, в момент времени t = 0 вектор A составляет с осью X угол0, определяемый условием
|
|
|
пр A(t 0) |
|
|
|
|
|
|
|||
tg 0 |
|
|
y |
0) |
|
|
|
|
|
|
||
|
|
|
прx A(t |
|
|
|
|
|
||||
|
|
|
|
|
|
|
(t 0) |
|
||||
|
прy A1(t 0) |
прy A2 |
|
|||||||||
|
|
|
|
|
|
(t 0) |
||||||
|
прx A1(t 0) |
прx A2 |
|
|||||||||
|
A1 sin 01 A2 sin 02 |
|
|
|
|
|||||||
|
A cos |
01 |
A cos |
02 |
|
|
|
|||||
|
1 |
|
|
|
2 |
|
|
|
|
|||
Таким образом, при сложении двух однонаправленных гармонических колебаний
x1 A1 cos( t 01 ) и x2 A2 cos( t 02 )
одинаковой частоты (такие колебания называются когерентными) получается гармоническое колебание той же частоты, амплитуда A и начальная фаза 0 которого определяются по приведенным выше формулам:
x x1 x2 A1 cos( t 01 ) A2 cos( t 02 ) Acos( t 0 )
На рисунке приведен пример сложения двух гармонических колебаний разных частот, амплитуд и начальных фаз
x1 |
|
t |
|
|
2cos |
|
; |
||
|
|
|
4 |
|
x2 |
|
|
|
|
3cos |
3 |
|
||
|
|
|
|
|
а также суммарное
колебание x1 + x2 (обозначено черным цветом)
При сложении однонаправленных гармонических колебаний с разными частотами
x1 A1 cos( 1t 01 );
x2 A2 cos( 2t 02 )
векторы A1 и A2 на векторной диаграмме вращаются вокруг точки O с разными ( 1 и 2) угловыми скоростями, поэтому вектор A = A1 + A2 деформируется со временем, т.е. движение системы не будет являться гармоническим колебанием.
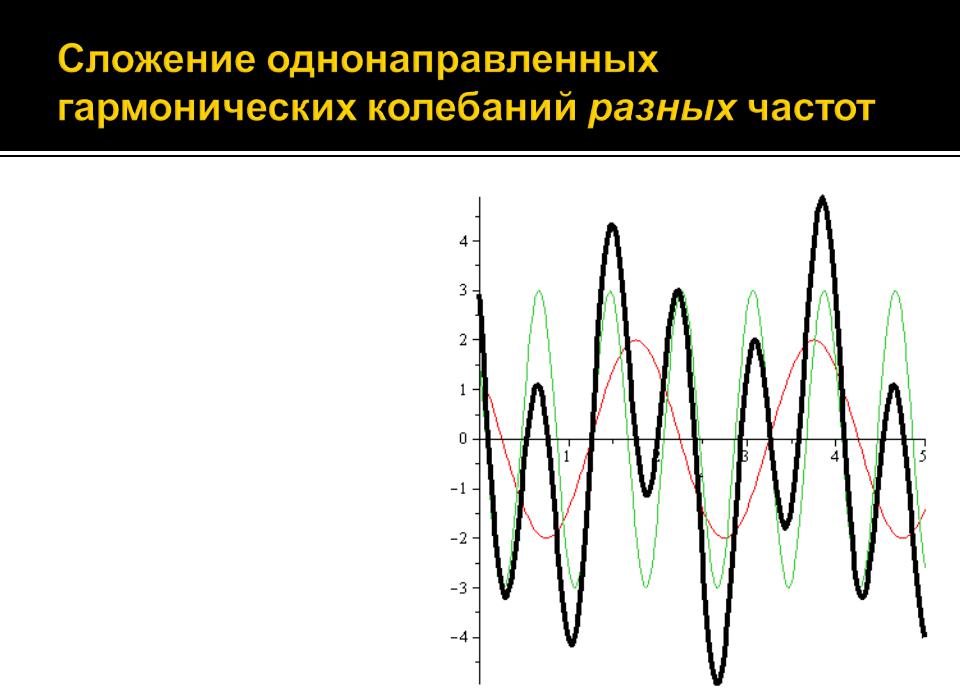
На рисунке приведен пример сложения двух гармонических колебаний разных частот, амплитуд и начальных фаз
x1 |
|
t |
|
|
|
2cos |
4 |
; |
|
||
|
|
|
|
|
|
x2 |
|
2,5 |
|
||
3cos |
3 |
|
|||
|
|
|
|
|
|
а также суммарное
колебание x1 + x2 (обозначено черным цветом)
Однако при сложении колебаний с близкими частотами
x1 A1 cos t 01 ;
x2 A2 cos ( ) 02 ;2 1 1 , 2
на промежутке времени = 2 / колебания можно считать когерентными. В результате сложения таких колебаний получается колебание, происходящее с частотой = ( 1 + 2)/2,
а их амплитуда A меняется от Amax = A1 + A2 до Amin = | A1 – A2 |. Такие колебания называют биениями, Б = –частотой
биений, а TБ = 2 / Б = 2 / – периодом биений.
Получим уравнение биений для частого случая, когда A1 = A2 =
A0:
x x1 x2 |
Acos( t 01 ) Acos(( )t 01 ) |
|
|
||||
t 01 t t 02 |
t 01 t t 02 |
|
|
||||
2Acos |
|
|
|
cos |
|
|
|
|
|
|
|||||
|
2 |
|
2 |
|
|||
|
|
|
|
|
|||
|
|
|
01 02 |
|
|
|
01 02 |
|
|
2Acos |
|
t |
|
cos |
срt |
|
. |
||
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
||||
Если при этом начальные фазы колебаний одинаковы ( 01 = 02 =0), то уравнение биений можно привести к виду:
|
|
|
|
x 2Acos |
2 |
t cos срt 0 |
|
|
|
|
|
|
|
|
|
x 2Acos |
2 |
t cos срt 0 |
|
|
|
|
|
Модуль первого множителя в формуле называется амплитудой биений.
Это медленно меняющаяся со временем величина:
Найдем период биений: |
|
|
|
|
|
||||
|
AБ |
2Acos |
2 |
t |
|
|
|
|
|
AБ |
|
|
|
|
max |
t |
n, n Z; |
|
|
|
|||||||
|
2Acos |
2 |
t |
|
2 |
|||
|
|
|
|
|
|
|
||
t 2 n TБ tmin 2
|
|
|
|
x 2Acos |
2 |
t cos срt 0 |
|
|
|
|
|