ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Если смещение консервативной механической системы из положения устойчивого равновесия описывается одним параметром x, то при малых x потенциальную энергию можно разложить в ряд:
(x) (x 0) |
x |
d |
|
1 |
x |
2 |
d 2 |
|
1 |
3 |
d 2 |
... |
|||||
|
|
|
|
|
|
|
|
x |
|
|
|
||||||
|
|
|
2 |
|
|
|
dx |
2 |
|
6 |
|
|
dx |
2 |
|
||
|
|
|
dx x 0 |
|
|
|
|
x 0 |
|
|
|
x 0 |
|
||||
Потенциальную энергию колебательной системы принято отсчитывать от положения устойчивого равновесия, в котором
(x = 0) = 0, (d /dx)x=0 = 0 (в положении устойчивого равновесия потенциальная энергия имеет минимум).
Таким образом, при малых смещения из положения устойчивого равновесия:
(x) (x 0) |
|
1 |
2 |
d 2 |
|
x2 |
||
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
dx |
2 |
|
2 |
|
|
|
|
x 0 |
|
|||
Система совершает гармонические колебания.
При этом величину –d /dx = Fx называют обобщенной силой, которая при малых x пропорциональна смещению: Fx = – x.
Если x – координата, то обобщенная сила – проекция силы F на направление X; если x – угол отклонения , то обобщенная сила – вращательный момент M.
В этом случае уравнение движения тела имеет вид:
mx x
(такой же вид, как и уравнение движения груза на пружине в отсутствие сил трения и сопротивления). Поэтому в этом случае силу Fx = – x называют квазиупругой, а коэффициент –
эффективной жесткостью.
Если сравнить уравнение движения с уравнением гармонических колебаний
x 2 x 0
то видно, что циклическая частота и период колебаний соответственно равны = ( /m)1/2 и T = 2 (m/ )1/2.
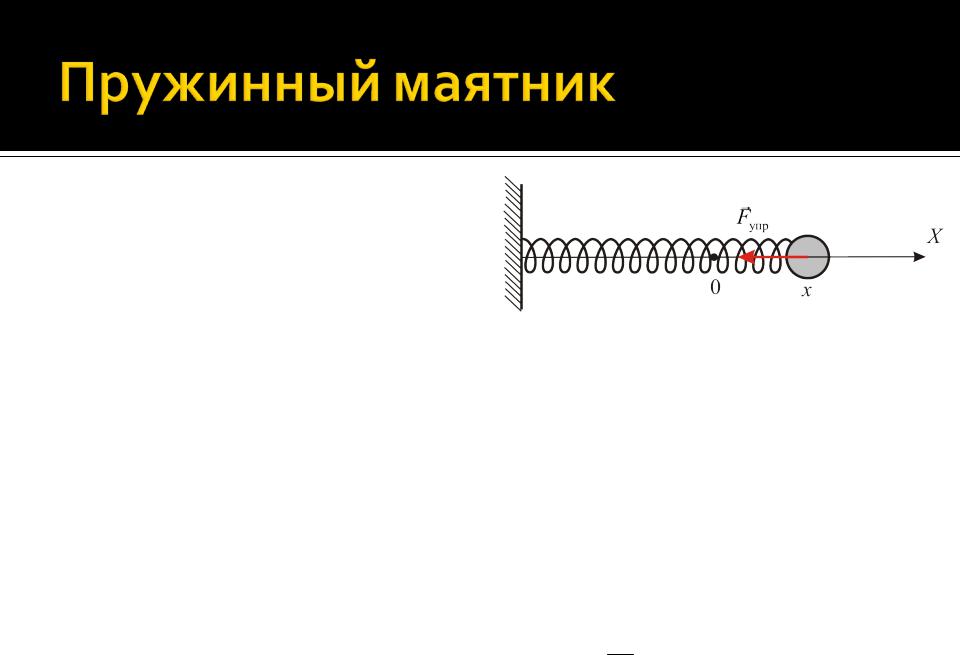
Рассмотрим спиральную пружину жесткостью k, один конец которой закреплен неподвижно, а к другому прикреплено тело (материальная точка массы m), которое может двигаться в горизонтальном направлении без трения или сопротивления.
Примем за начало координат положение тела, при котором пружина недеформирована
На тело действует сила упругости, направленная к положению равновесия. Таким образом, уравнение движения тела:
max Fупр,x mx kx
x mk x 0
x mk x 0
Сравнивая это уравнение с дифференциальным уравнением гармонических колебаний,
x 2 x 0
находим, что собственная циклическая частота и
период T гармонических колебаний пружинного маятника соответственно равны:
mk
T 2 
mk
Если точка совершает гармонические колебания по закону |
x = |
||||||||||||||||||
Acos( t + 0), то ее потенциальная и кинетическая энергии |
|
||||||||||||||||||
изменяются также по гармоническому закону с частотой 2 : |
|
||||||||||||||||||
|
x2 |
|
|
A2 |
cos2 ( t 0 ) |
A2 |
[1 cos(2 t 2 0 )] 1 |
E[1 cos(2 t 2 0 )]; |
|
||||||||||
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
mx2 |
|
|
|
m 2 |
A2 |
|
m 2 |
A2 |
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
sin2 ( t 0 ) |
|
|
|
|
[1 cos(2 t 2 |
0 )] |
|
E[1 cos(2 t 2 0 )]. |
||||
|
2 |
|
2 |
|
4 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь учтено, что = ( /m)1/2 и |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
E |
A2 |
m 2 A2 |
max max |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. при гармонических колебаниях полная механическая энергия точки сохраняется.
Математический маятник –
подвешенное на невесомой нерастяжимой нити тело (материальная точка), способное под действием приложенных к нему сил (обычно – силы тяжести) совершать колебания около положения равновесия.
Выведем маятник длиной l с телом массы m из положения равновесия, отклонив нить на малый угол .
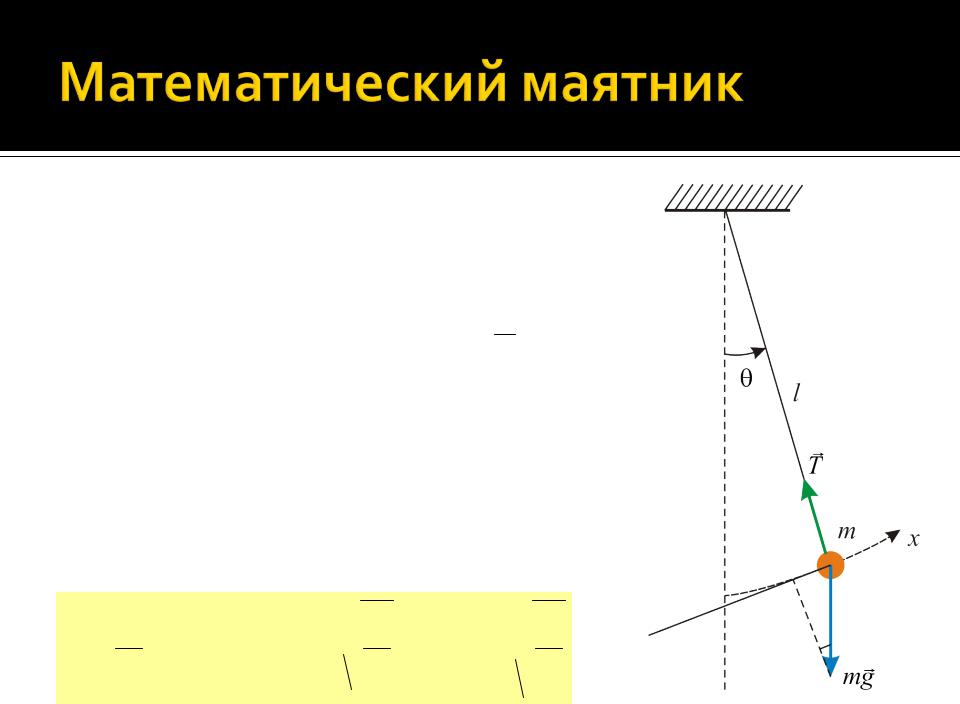
Спроецируем уравнение движения (2 закон Ньютона ma = mg + T на направление дуговой координаты x):
mx mg sin mg mg x |
|
|
l |
(угол мал, << 1). Приведем |
|
полученное уравнение к виду дифференциального уравнения гармонических колебаний, найдем циклическую частоту и период колебаний математического маятника:
x gl x 0 
gl ;T 2 
gl
Поскольку x = l , то дифференциальное
уравнение гармонических колебаний математического маятника, а также его решение (угол отклонения маятника
от положения равновесия) выглядят следующим образом:
gl 0;
g |
|
l 0
Здесь max и 0 – амплитуда и начальная
фаза колебаний, определяемые начальными условиями.tcos