ЛЕКЦИЯ 1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Колебания – это такое изменения состояния системы, при котором ее параметры меняются со временем по периодическому (или почти периодическому) закону.
Колебания называются периодическими, если значения физических величин (параметров системы) повторяются через одинаковые промежутки времени.
Период колебаний T – тот наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебательное движение.
За время, равное периоду, совершается одно полное колебание
Частотой (линейной частотой) периодических колебаний называют число колебаний, совершаемых за единицу времени:
T1
Частота колебаний измеряется в герцах (Гц): [ ] = Гц = с-1.
Колебания величины x называются гармоническими, если эта величина меняется со временем t по закону:
x Acos( t 0 )
Величина A (измеряется в тех же единицах, что и x) – амплитуда колебаний – максимальное отклонение колеблющейся величины x от положения устойчивого равновесия (A = max x).
– циклическая (круговая) частота колебаний (определяется только параметрами системы); [ ] = c-1.
2 2
T
xAcos( t 0 )
Величина = t + 0 называется фазой колебаний. Косинус (или синус) этой величины показывает, во сколько раз значение физической величины x меньше его амплитудного (максимального) значения в данный момент времени.
Величина 0 = (t = 0) называется начальной фазой колебаний.
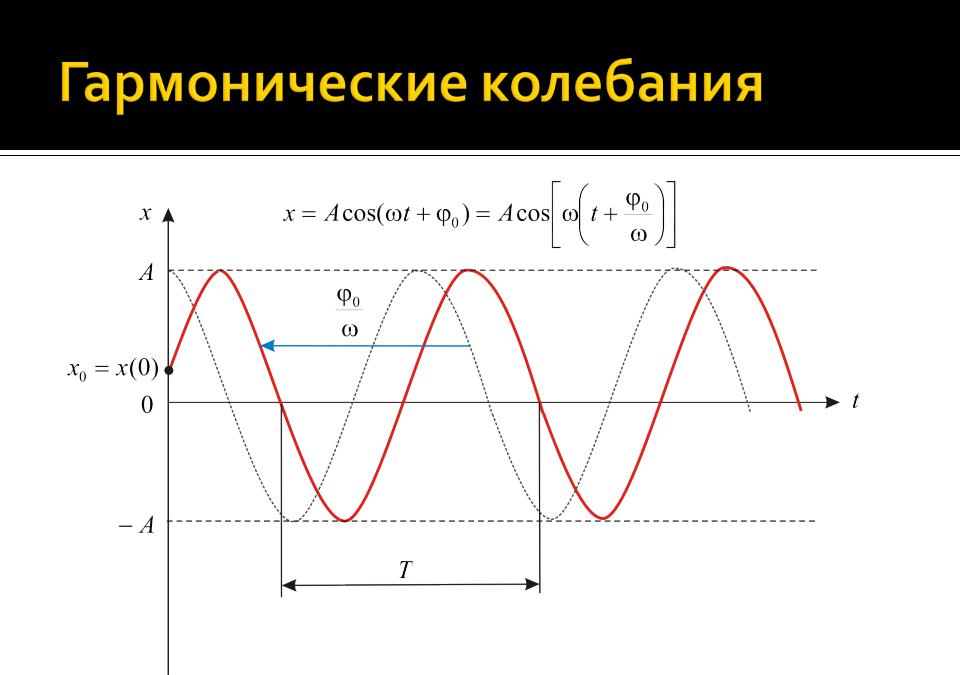
xAcos( t 0 )
Найдем первую и вторую производные по времени t от колеблющейся физической величины x:
x A sin( t |
) A cos |
t |
0 |
|
; |
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x A 2 |
cos( t |
) A 2 cos( t |
0 |
) 2 x. |
||||
|
|
0 |
|
|
|
|
|
|
Таким образом, эти величины совершают гармонические колебания с той же частотой , но с амплитудами A и 2A и со сдвигом по фазе на /2 и соответственно.
x Acos( t 0 )
x A 2 cos( t 0 ) 2 x.
Как видно из приведенного уравнения, если физическая величина x изменяется по закону гармонических колебаний, то она удовлетворяет дифференциальному уравнению гармонических колебаний:
x 2 x 0
Гармоническое колебание можно представить графически с помощью вращающегося вектора-амплитуды.
Вектор A, равный по модулю амплитуде A колебаний, равномерно вращается против часовой стрелки вокруг оси O, перпендикулярной плоскости чертежа, с угловой скоростью , равной круговой частоте
колебаний. Если в момент времени t = 0 угол между вектором A и осью OX
равен 0, то проекция этого вектора на ось OX совершает гармонические колебания по закону x = Acos( t + ).