Стоячая волна образуется при наложении двух плоских волн одинаковой частоты и амплитуды, распространяющихся навстречу друг другу:
1,2 Acos( t kx 01,2 )
При наложении двух волн любая частица среды одновременно участвует в двух колебательных движениях, описываемых этими уравнениями. Результирующее смещение частицы из
положения равновесия равно сумме смещений 1 и 2, вызванных каждой из бегущих волн:
1 2
41
Уравнение волны, образующейся в результате наложения двух плоских волн, т.е. уравнение стоячей волны:
1 2 |
A[cos( t kx 01 ) cos( t kx 02 )] |
|||||||
|
|
02 01 |
|
|
|
01 02 |
|
|
2Acos kx |
|
cos |
t |
|
|
|||
2 |
2 |
|||||||
|
|
|
|
|
|
|||
Изменим начало отсчета координаты x и момента начала времени t, заменив переменные:
x x |
02 01 |
; |
t t |
01 02 |
|
2k |
2 |
||||
|
|
|
42
Тогда уравнение бегущей волны в переменных x и t примет вид:
2Acos kx cos t
Таким образом показано, что уравнение стоячей волны всегда может быть приведено к виду
2Acos kx cos t
Из уравнения видно, что частицы упругой среды совершают гармонические колебания с циклической частотой , амплитуда которых |2Acoskx| зависит от координаты x положения равновесия колеблющейся частицы.
43
Пучности стоячей волны – это точки пространства, которые являются положениями равновесия частиц среды, совершающих колебания с максимальной амплитудой (2A)
Максимальное значение амплитуды |2Acoskx| достигается при условии: |coskx| = 1, из которого можно определить положение пучностей в пространстве:
x(пуч.) n n , n 0,1,2,...
k 2
Расстояние между двумя соседними пучностями равно половине длины волны: x(пуч.) = /2.
44
Узлами стоячей волны называются точки пространства, которые являются положения равновесия частиц упругой среды с нулевой амплитудой колебаний (0).
Амплитуда |2Acoskx| = 0 достигается при условии: |coskx| = 0, из которого можно определить положение узлов в пространстве:
x(узл.) (2n 1) n
k 2
1 , n 0,1,2,...
2 2
Расстояние между двумя соседними узлами равно половине длины волны: x(узл.) = /2.
45
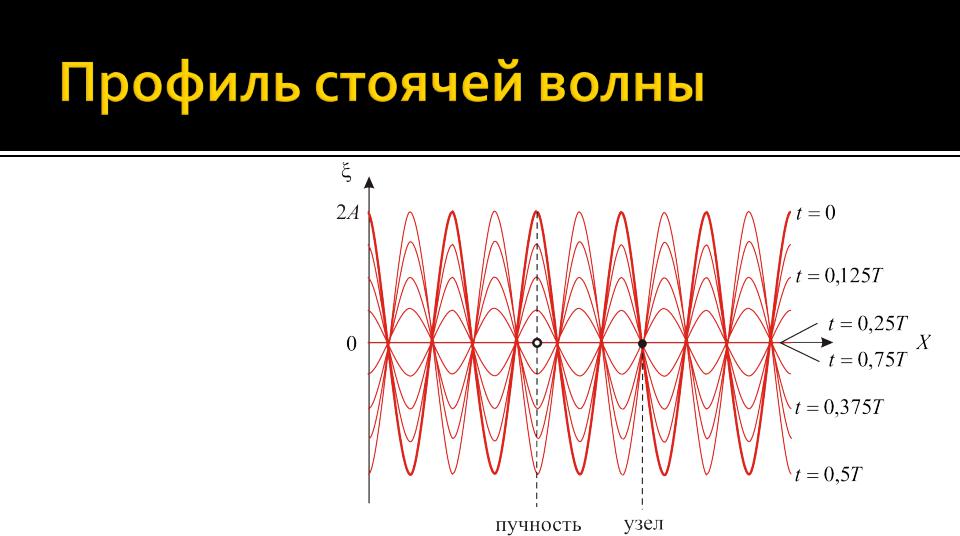
На рисунке представлен профиль стоячей волны в разные моменты времени, разделенные промежутком в 1/16 периода колебаний T.
Видно, что частицы, расположенные в узлах, не колеблются, а частицы пучностей волны – колеблются с максимальной амплитудой.
2Acos kx cos t
46
Можно показать, что за период колебаний дважды происходит превращение энергии стоячей волны из полностью потенциальной, сосредоточенной вблизи узлов волны, в полностью кинетическую, сосредоточенную в основном вблизи пучностей волны.
В результате энергия переходит от каждого узла к соседним с ним пучностям и обратно. Средний по времени поток энергии, переносимой стоячей волной, в любом перпендикулярном оси X сечении волны равен нулю (в стоячей волне нет переноса энергии)
47