
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Относительность
- •Система координат
- •Координаты тела
- •Измерение длины
- •Измерение длины
- •Измерение длины
- •Измерение времени
- •Синхронизация часов
- •Пространственно-временная система отсчета
- •Постулаты классической механики о пространстве,
- •Постулаты классической механики о пространстве,
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Кинематика. Выбор системы отсчета
- •Понятие материальной точки
- •Понятие материальной точки
- •Векторный способ задания движения
- •Траектория. Перемещение
- •Вектор средней скорости
- •Мгновенная скорость
- •Единица измерения скорости
- •Ускорение
- •Прямая и обратная задачи кинематики
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Координатный способ задания движения
- •Закон движения
- •Скорость при координатном способе описания движения
- •Модуль и направление вектора скорости
- •Ускорение при координатном способе
- •Модуль и направление вектора ускорения
- •Путь
- •Связь между путем и модулем скорости частицы
- •Связь между путем и модулем скорости частицы
- •Связь между путем и модулем скорости частицы
- •Графическое определение пути
- •Полное ускорение частицы
- •Полное ускорение частицы
- •Тангенциальное (касательное) ускорение
- •Нормальное
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Абсолютно твердое тело
- •Виды движения абсолютно твердого тела
- •Поступательное движение абсолютно твердого тела
- •Вращение абсолютно твердого тела вокруг
- •Плоское движение абсолютно твердого тела
- •Вращение абсолютно твердого тела
- •Свободное движение абсолютно твердого тела
- •Число степеней свободы
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Угловая координата
- •Угловая координата
- •Вектор элементарного поворота
- •Угловая скорость
- •Угловое ускорение
- •Угловое ускорение
- •Связь между линейными и угловыми кинематическими
- •Связь между линейными и угловыми кинематическими
- •Линейная скорость точки АТТ
- •Угловое ускорение точки АТТ
- •Угловое ускорение точки АТТ
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Плоское движение твердого тела
- •Описание плоского движения твердого тела
- •Линейная скорость точки твердого тела при его
- •Мгновенная ось вращения
- •Вращение твердого тела вокруг неподвижной точки. Свободное
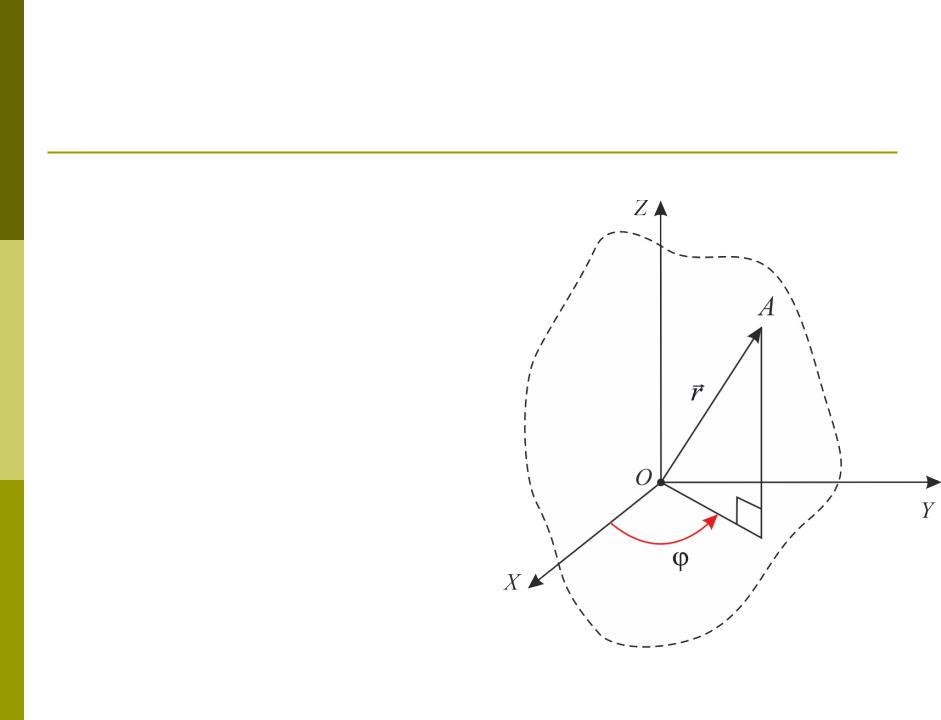
Угловая координата
Угол поворота – величина скалярная, он может быть положительным, отрицательным или равным нулю
Положительное направление угла поворота определяется по
правилу правого винта: оно образует правый винт с положительным направлением оси Z декартовой системы координат.
Угол поворота измеряется в
радианах (рад).
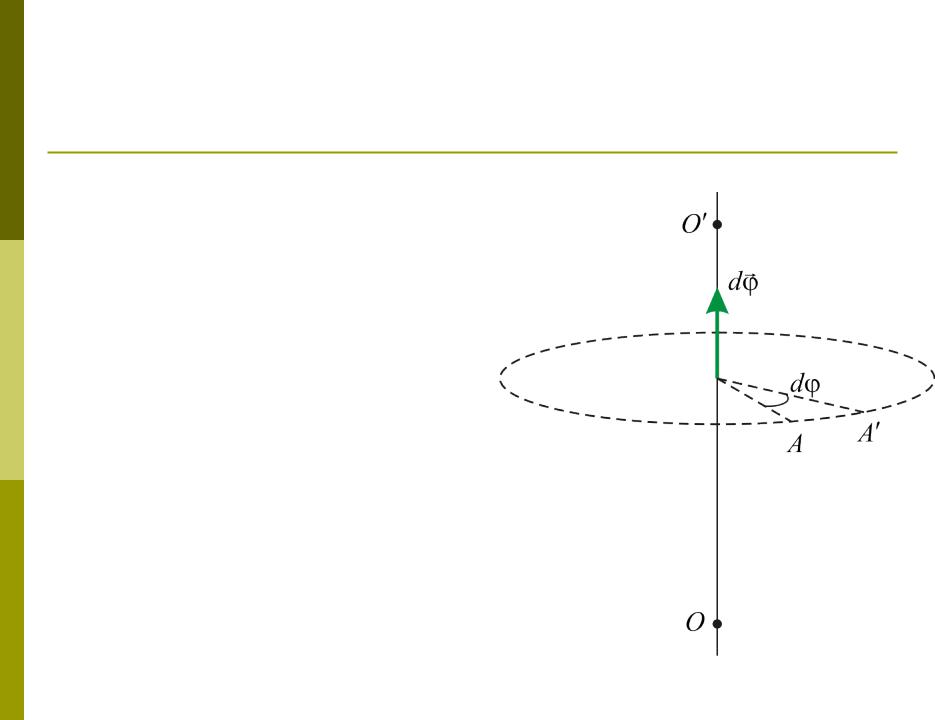
Вектор элементарного поворота
Пусть тело повернулось на бесконечно малый угол d вокруг оси Z за время dt. При этом точка A, двигаясь по
окружности, заняла положение
A .
Вектором элементарного поворота называется вектор d , модуль которого равен углу d : |d | = d ; этот вектор направлен вдоль оси вращения тела, при этом направление d связано правилом правого винта с направлением вращения тела.

Угловая скорость
Пусть тело, вращаясь вокруг оси Z, совершило за малый промежуток времени dt элементарный поворот d .
Угловой скоростью тела называется вектор
ddt
Вектор совпадает по направлению с вектором d , т.е. направлен вдоль оси вращения тела так, что образует правый винт с направлением вращения.
Проекция вектора на ось Z и его модуль:
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d |
; |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
dt |
dt |
|
|
dt |
||||||||
|
|
|
|
|
|
|
|
|
||||
Единица измерения – радиан в секунду (рад/с)

Угловое ускорение
Угловым ускорением называется вектор, равный производной угловой скорости тела по времени:
d
dt
Проекция вектора углового ускорения на ось вращения Z:
z d z d 2 2 dt dt
Единица углового ускорения в системе СИ – радиан на секунду в квадрате (рад/с2)
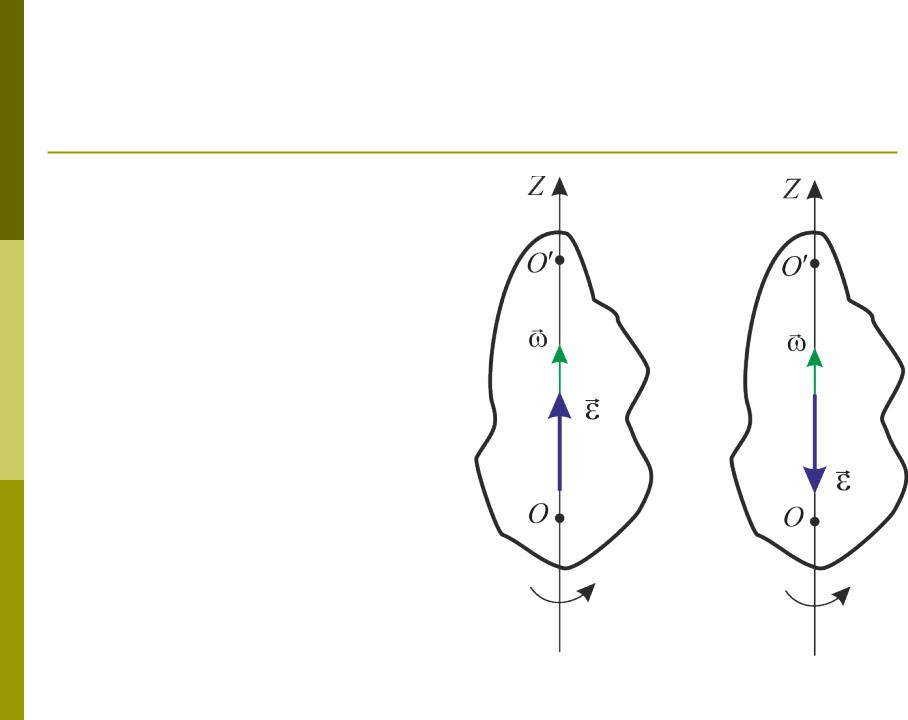
Угловое ускорение
Направление вектора совпадает с направлением вектора d приращения вектора угловой скорости за бесконечно малый промежуток времени dt.
Если с течением времени модуль вектора увеличивается (тело вращается ускоренно), то; если же модуль вектора уменьшается (тело вращается замедленно), то .

Связь между линейными и угловыми кинематическими
величинамиПостановка задачи. Пусть твердое тело вращается вокруг неподвижной оси Z с угловой
скоростью и угловым ускорением .
Найдем связь между линейными величинами – скоростью vA и ускорением aA произвольной точки A тела с угловыми величинами – угловой скоростью и угловым ускорением тела
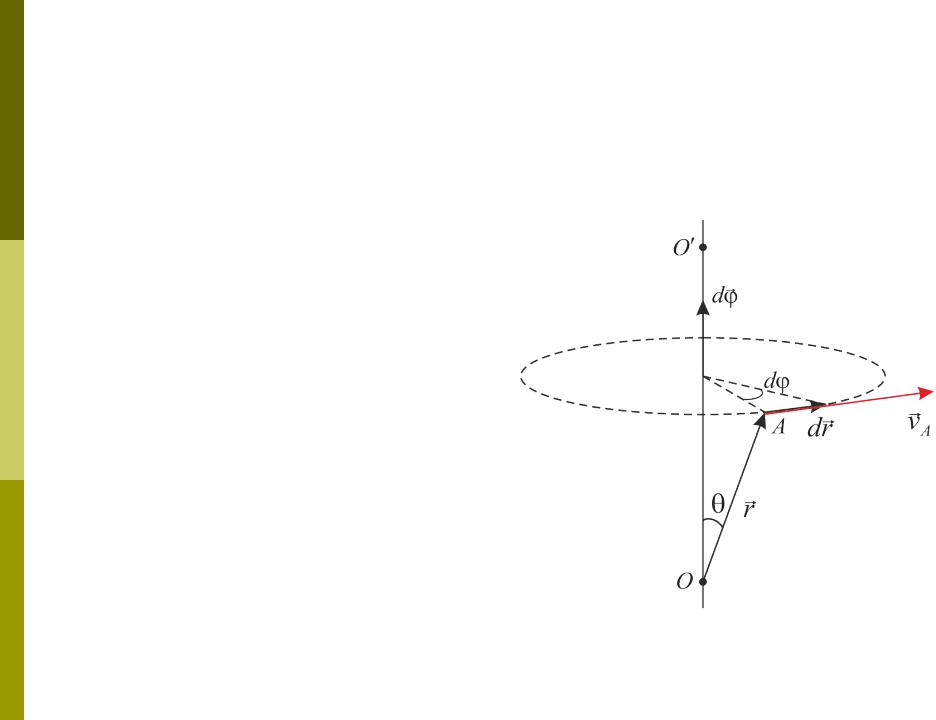
Связь между линейными и угловыми кинематическими
величинамиПоложение точки A зададим ее радиусом-вектором r,
проведенным из произвольной точки на оси вращения.
Угол между осью вращения и r |
|
обозначим . |
R |
За бесконечно малый промежуток времени dt тело совершает элементарный поворот d . При этом точка A, двигаясь по окружности радиуса R = rsin с центром на оси вращения, совершает элементарное перемещение dr.
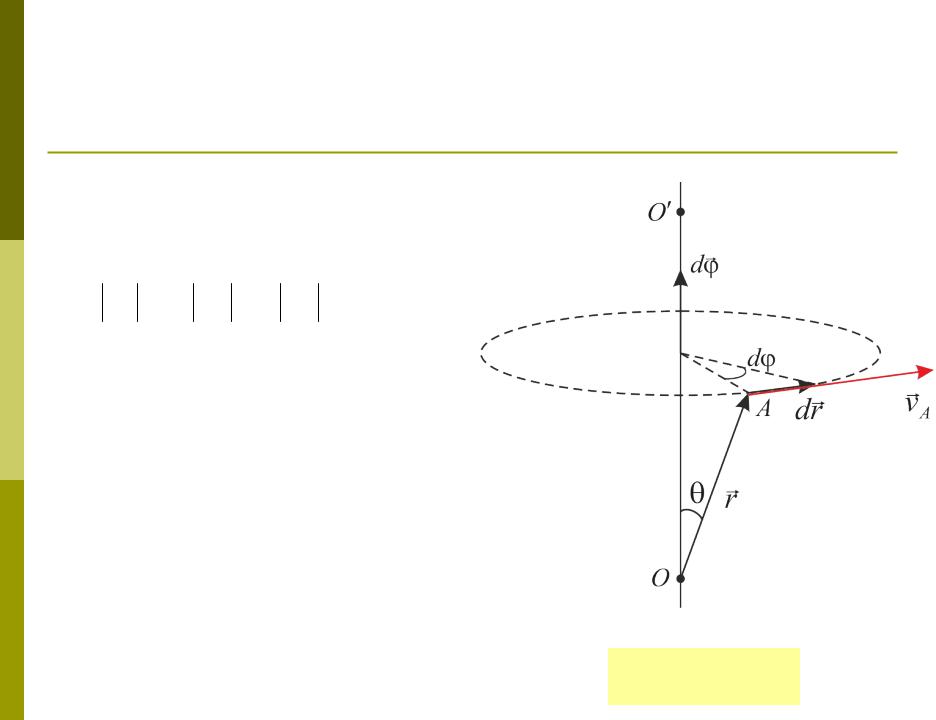
Линейная скорость точки АТТ
Модуль элементарного перемещения точки A:
dr R d r d sin
или в векторной форме: dr [d r ]
Тогда скорость точки A:
dr |
|
d |
|
|
|
vA |
|
|
|
[ r ] |
|
dt |
|
|
r |
||
|
dt |
|
|
||
vA [ r ]

Угловое ускорение точки АТТ
Найдем теперь выражение для ускорения точки A. Согласно определению ускорения,
|
dvA |
|
d |
|
d |
|
|
|
dr |
|
|
|
|
|
||
aA |
|
|
|
[ r ] |
|
r |
|
|
[ r ] [ vA ] [ r ] [ [ r ]] |
|||||||
dt |
dt |
dt |
||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||||
Первое слагаемое – это тангенциальное ускорение:
a [ r ] |
a r sin R |
Второе слагаемое – это нормальное ускорение:
an [ [ r ]] |
a 2r sin |
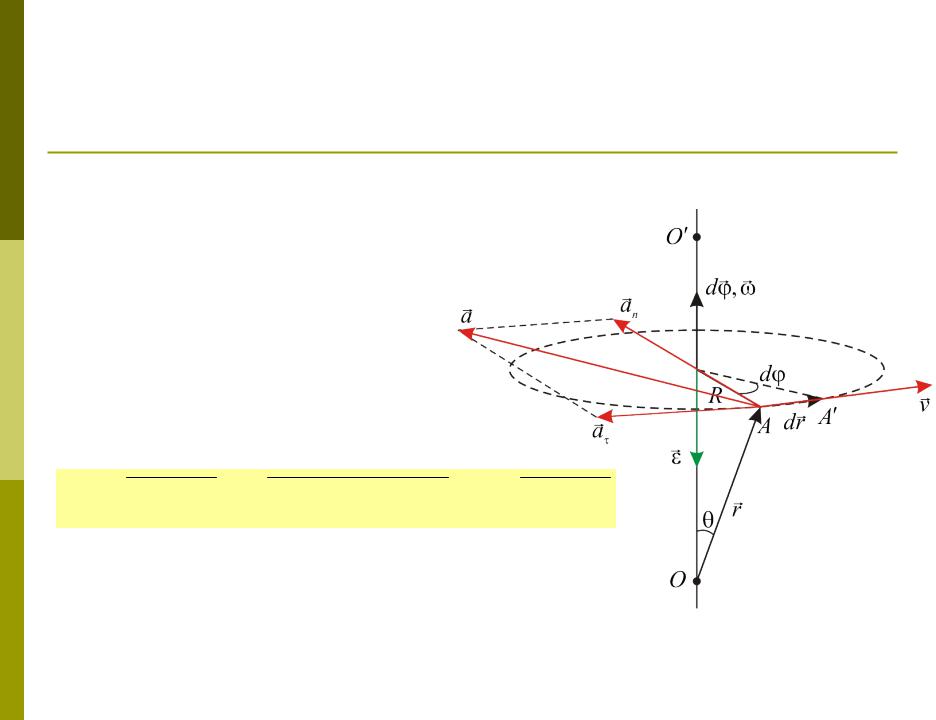
Угловое ускорение точки АТТ
Таким образом, полное ускорение точки A твердого тела:
a 
 a2 an2
a2 an2 
 ( R)2 ( 2 R)2 R
( R)2 ( 2 R)2 R
 2 4
2 4
