
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Относительность
- •Система координат
- •Координаты тела
- •Измерение длины
- •Измерение длины
- •Измерение длины
- •Измерение времени
- •Синхронизация часов
- •Пространственно-временная система отсчета
- •Постулаты классической механики о пространстве,
- •Постулаты классической механики о пространстве,
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Кинематика. Выбор системы отсчета
- •Понятие материальной точки
- •Понятие материальной точки
- •Векторный способ задания движения
- •Траектория. Перемещение
- •Вектор средней скорости
- •Мгновенная скорость
- •Единица измерения скорости
- •Ускорение
- •Прямая и обратная задачи кинематики
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Координатный способ задания движения
- •Закон движения
- •Скорость при координатном способе описания движения
- •Модуль и направление вектора скорости
- •Ускорение при координатном способе
- •Модуль и направление вектора ускорения
- •Путь
- •Связь между путем и модулем скорости частицы
- •Связь между путем и модулем скорости частицы
- •Связь между путем и модулем скорости частицы
- •Графическое определение пути
- •Полное ускорение частицы
- •Полное ускорение частицы
- •Тангенциальное (касательное) ускорение
- •Нормальное
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Абсолютно твердое тело
- •Виды движения абсолютно твердого тела
- •Поступательное движение абсолютно твердого тела
- •Вращение абсолютно твердого тела вокруг
- •Плоское движение абсолютно твердого тела
- •Вращение абсолютно твердого тела
- •Свободное движение абсолютно твердого тела
- •Число степеней свободы
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Угловая координата
- •Угловая координата
- •Вектор элементарного поворота
- •Угловая скорость
- •Угловое ускорение
- •Угловое ускорение
- •Связь между линейными и угловыми кинематическими
- •Связь между линейными и угловыми кинематическими
- •Линейная скорость точки АТТ
- •Угловое ускорение точки АТТ
- •Угловое ускорение точки АТТ
- •ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
- •Плоское движение твердого тела
- •Описание плоского движения твердого тела
- •Линейная скорость точки твердого тела при его
- •Мгновенная ось вращения
- •Вращение твердого тела вокруг неподвижной точки. Свободное

Единица измерения скорости
В СИ скорость измеряется в метрах в секунду (м/с).
1 км/ч = 1000 м/3600 с = 0,36 м/с
21

Ускорение
Ускорением называется вектор, равный производной по времени скорости v частицы:
|
|
|
dv |
d 2 r |
|
a |
dt |
dt 2 |
22

Прямая и обратная задачи кинематики
Если зависимость радиуса-вектора от времени r(t) известна, то можно решить т.н. прямую задачу кинематики – определить скорость v и ускорение a частицы в любой момент времени t.
Обратная задача кинематики состоит в том, чтобы зная зависимость от времени ускорения a(t) и
начальные условия движения (скорость v0 и радиус- вектор r0 в начальный момент времени t = 0), определить в любой момент времени скорость v и положение r частицы в пространстве.
23

ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ
1.3 Координатный способ описания движения материальной точки
24
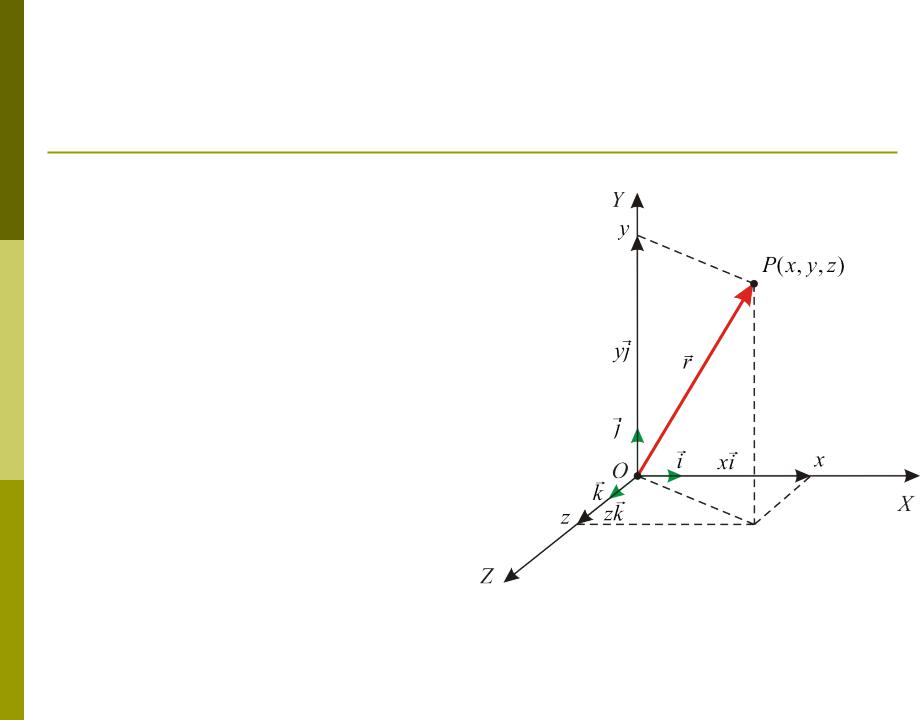
Координатный способ задания движения
Для описания движения частицы P в пространстве выберем некоторое тело отсчета, с которым свяжем декартову систему координат (далее – ДСК).
Положение частицы в пространстве при
координатном способе
описания движения задается ее координатами
x, y, z (координаты |
|
радиуса-вектора r). |
25 |

Закон движения
Законом движения называется зависимость от времени координат частицы:
x x(t), y y(t), z z(t)
Между векторным и координатным способами описания движения существует простая связь. Любой вектор можно задать его проекциями на оси координат. Например, радиус-вектор частицы:
r xi yj zk
где i, j, k – орты координатных осей.
26

Скорость при координатном способе описания движения
Скорость v, как и любой вектор, может быть представлена через проекции на оси ДСК:
v vx i vy j vz k
Т.о., скорость v частицы можно представить в следующем виде:
|
dr |
|
d |
|
|
|
dx |
dy |
dz |
v(t) dt |
|
|
(xi |
yj |
zk ) dt i |
dt j |
dt k |
||
dt |
|||||||||
Видно, что компоненты скорости, выраженные через функции x(t), y(t), z(t), равны
vx dx |
, vy dy |
, vz dz |
27 |
dt |
dt |
dt |
|
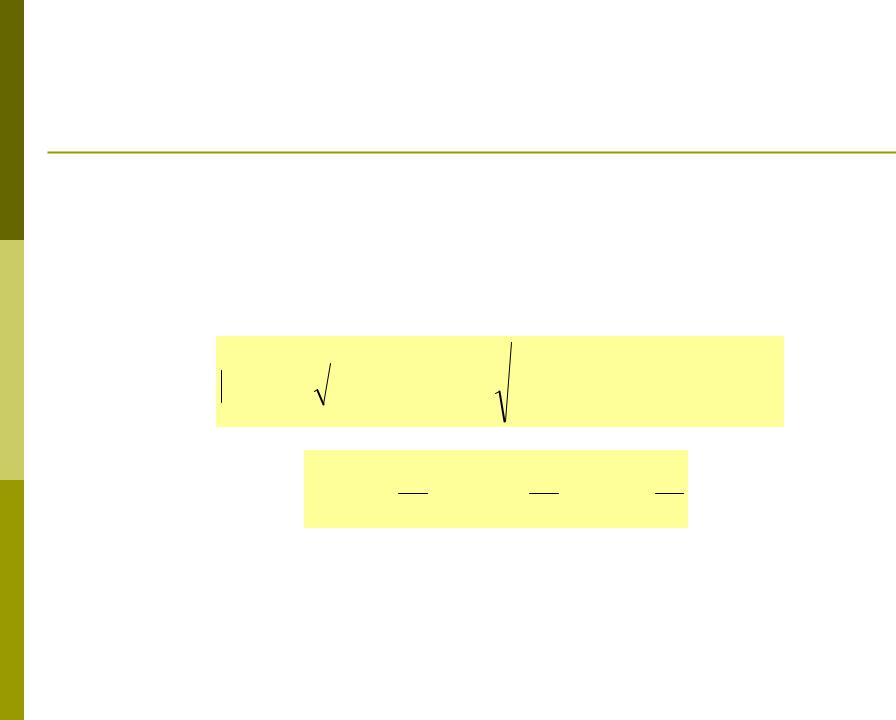
Модуль и направление вектора скорости
Для каждого момента времени t можно определить модуль и направление (с помощью
направляющих косинусов) вектора скорости v:
|
|
|
|
|
|
|
dx 2 |
dy 2 |
dz 2 |
|||
|
v |
2 |
2 |
2 |
|
|||||||
|
||||||||||||
v |
|
vx |
vy |
vz |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dt |
|
dt |
dt |
|
|
|
|
|
|
|
|
||||||
cos vvx , cos vvy , cos vvz
Здесь , , – углы, образованные вектором v с осями X, Y и Z соответственно
28

Ускорение при координатном способе
заданияУскорение a, какдвиженияи любой вектор, может быть представлен через проекции на оси ДСК:
a ax i ay j az k
Т.о., скорость v частицы можно представить в следующем виде:
|
|
|
d |
|
|
|
dv |
|
|
dvy |
|
dv |
|
|
dv |
|
x |
z |
|||||||||||
a(t) |
|
|
|
(vx i |
vy j |
vz k ) |
|
i |
|
j |
|
k |
||
dt |
dt |
|
|
dt |
|
|
||||||||
|
|
|
|
|
dt |
|
dt |
|||||||
Видно, что компоненты скорости, выраженные через функции x(t), y(t), z(t), равны
ax |
dv |
x |
d 2 x |
, ay |
dvy |
|
d 2 y |
, az |
dv |
z |
d 2 z |
|
|
dt 2 |
dt |
dt |
2 |
|
dt 2 |
||||||
|
dt |
|
|
|
dt |
|||||||
29
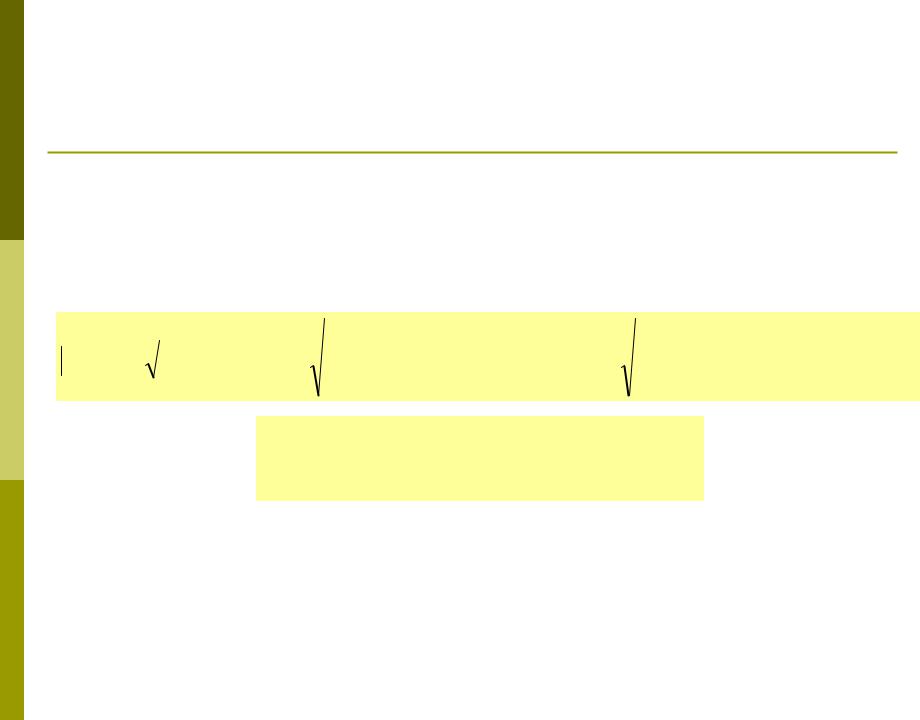
Модуль и направление вектора ускорения
Для каждого момента времени t можно определить модуль и направление (с помощью направляющих косинусов)
вектора ускорения a:
|
|
|
|
|
|
|
|
|
|
dvx 2 |
dvy |
2 |
dvz |
2 |
|
d |
2 x |
2 |
d 2 y 2 |
d 2 z 2 |
||||||||||||||||
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
a |
|
a |
a |
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
x |
|
y |
|
z |
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
2 |
|
|
|
dt |
2 |
|
dt |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
cos |
a |
x |
, cos |
ay |
, cos |
a |
z |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
a |
a |
|
a |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь , , – углы, образованные вектором a с осями X, Y и Z соответственно
30
