13.6. Расчет подводящего (всасывающего) трубопровода центробежного насоса

Всасывающий трубопровод обычно - гидравлически короткий трубопровод (рис. 13.6), в котором должны быть учтены при расчете как потери по длине, так и детально местные потери напора. В таком трубопроводе вследствие работы центробежного насоса на входе в него (в сечении 2-2) возникает разрежение (вакуум), благодаря чему жидкость течет по трубопроводу к насосу.

Рис. 13.6

Цель расчета рассматриваемого трубопровода состоит в определении высоты установки насоса или вакуумметрической высоты во всасывающем патрубке центробежного насоса.

Запишем уравнение Бернулли для сечений 1-1 и 2-2, причем первое сечение выбрано на поверхности воды в водоеме (питателе), а второе -непосредственно перед входом в насос во всасывающем патрубке. Плоскость сравнения совмещена с сечением 1-1. Расход , подаваемый насосом, известен. Диаметр всасывающего трубопровода определяется при заданном расходе с учетом рекомендуемой СНиП средней скорости движения воды в трубопроводах насосных станций (табл. 13.2).

Таблица 13 2

Зная и выбрав значение, найдем

.

Далее, приняв ближайший стандартный диаметр трубопровода, вновь находим среднюю скорость в трубопроводе и ее вводим в расчет.

Рассмотрим горизонтальный центробежный насос. Уравнение Бернулли имеет в данном случае вид

.

Отсюда высота установки насоса (геометрическая высота всасывания) при

.

Геометрическая высота всасывания для горизонтального центробежного насоса определяется от уровня в водоеме (от минимального уровня при изменениях этого уровня), до оси насоса.

Вакуумметрическая высота всасывания

.

Тогда

.

Допустимое значение приводится заводом-изготовителем, обычно м.

Следовательно, допустимая высота установки насоса должна быть меньше на, где.

С помощью уравнения Бернулли, естественно, можно решить и другую задачу: определить во всасывающем патрубке центробежного насоса при известной высоте установки насоса.

Допустимое значение зависит от конструкции насоса, рода и температуры перекачиваемой жидкости. Для нормальных условий работы насоса необходимо, чтобыпри данной температуре. Иначе может начаться интенсивное выделение паров жидкости и газов, нормальный режим работы насоса нарушится и подача уменьшится.

13.7. Расчет экономически наивыгоднейшего диаметра нагнетательного трубопровода

Центробежный насос создает напор, благодаря которому жидкость подается на более высокие отметки (рис. 13.7), например, в водонапорную башню, откуда вода поступает самотеком в распределительную сеть и раздается потребителям. Могут быть и другие схемы.

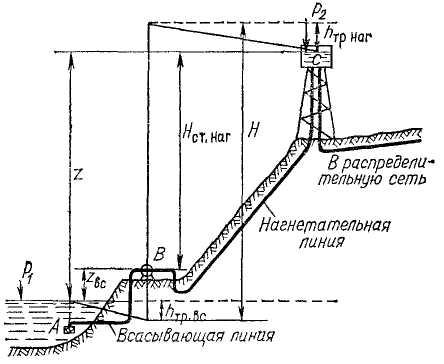
Рис. 13.7

Благодаря работе насоса каждая единица веса жидкости, пройдя через насос, получает дополнительно к той удельной энергии, которой эта единица веса обладала на входе в насос, определенную удельную энергию . Эта дополнительная удельная энергия называется напором насоса и обычно выражается в метрах столба перекачиваемой жидкости.

При подаче жидкости на высоту из питателя с давлениемна поверхности в резервуар-приемник с давлениемна поверхности напор равен (если)

,

где - скорость в резервуаре-приемнике.

Если , а скоростным напоромможно пренебречь, то для подъема жидкости должен быть создан напор

,

где - сумма геометрических высот всасывания и нагнетания; а- сумма потерь напора на преодоление гидравлических сопротивлений во всасывающем и нагнетательном трубопроводах.

Величину называют геодезической (нивелирной, статической) высотой подъема.

Таким образом, каждой единице веса жидкости насосом должна быть сообщена дополнительная удельная энергия, равная

.

Заданный расход жидкости может быть подан на требуемый уровень нагнетания (т. е. при заданной геодезической высоте подъема) по трубам различного диаметра.

При рассмотрении задачи выбора диаметра нагнетательного трубопровода неизвестны и диаметр , и напор. В выражении для напора можно отделить величины, не зависящие от диаметра нагнетательного трубопровода (), от потерь напора на преодоление гидравлических сопротивлений в нагнетательном трубопроводе.

При расходе жидкости (подаче насоса) и напореподводимая к двигателю насоса мощность

, (13.24)

где - расход (подача), м³/с; -напор, м;-коэффициенты полезного действия насоса и двигателя.

Обозначив , получим для воды, кВт,

. (13.25)

Часть этой мощности расходуется на подъем жидкости на геометрическую (геодезическую) высотуи на преодоление гидравлических сопротивлений во всасывающем трубопроводе. Все эти величины от диаметра нагнетательной линии не зависят.

Часть мощности, равная , предназначена для преодоления сопротивлений в нагнетательном трубопроводе и, понятно, существенно зависит от диаметра этого трубопровода. Рассчитываемые нагнетательные трубопроводы систем водоснабжения обычно относятся к гидравлически длинным и.

Оптимальный (экономически наивыгоднейший) диаметр нагнетательного трубопровода определяют на основе технико-экономических расчетов.

Потери напора по длине трубопровода обратно пропорциональны диаметру трубы в степени, близкой к пятой. Увеличивая диаметр трубы, можно заметно уменьшить потери напора, следовательно, уменьшить мощность и затраты на электроэнергию, предназначенную для создания этой части мощности.

Но увеличение диаметра труб приводит к увеличению строительной стоимости трубопровода (капиталовложений в строительство трубопровода) и ежегодных амортизационных (и других) отчислений.

И, наоборот, с уменьшением диаметра трубы резко возрастает стоимость электроэнергии, затрачиваемой на преодоление гидравлических сопротивлений, но уменьшаются строительная стоимость и ежегодные отчисления.

Отсюда ясно, что экономически наивыгоднейшим диаметром следует считать такой, при котором приведенные годовые затраты будут минимальными.

Приведенные годовые затраты на 1 м трубопровода определяются следующим образом:

(13.26)

Здесь - приведенные годовые затраты;- затраты на оплату электроэнергии, затрачиваемой на преодоление гидравлических сопротивлений (в нагнетательном трубопроводе) на длине 1 м:

,

где индекс штрих соответствует 1 м; - коэффициент полезного действия насосного агрегата (насосной установки);- число часов работы насосной станции (установки) в год, определяется с учетом изменения режима водопотребления и режима работы с изменением водоподачи;- тариф на электроэнергию для данного района (нормативная величина), р/(кВтч).

Выражение для строительной стоимости единицы длины трубопровода, найденное из анализа сметной стоимости строительства, имеет вид

,

где - постоянная (не зависящая от диаметра) часть строительной стоимости (табл. 13.3);- нормированный коэффициент, зависящий от вида труб и от условий строительства;- показатель степени, зависящий от вида труб и не зависящий от условий строительства.

Доля строительной стоимости 1 м трубопровода, отнесенная к одному году, равна

,

где - нормативный срок окупаемости капиталовложений в строительство; для водоснабжения принимается равным 7-10 годам.

Сумма амортизационных отчислений (в том числе отчислений на капитальный ремонт) и отчислений на текущий ремонт, отнесенная к одному году, равна

,

где - сумма нормированных отчислений в процентах (табл. 13.3).

Обозначим

.

Значения (при различных) по нормативным данным для труб из различных материалов приводятся в табл. 13.3.

Таблица 13.3

Трубы			при
Стальные Чугунные Асбоцементные Полиэтиленовые	4,6 3,3 7,3 4,6	6,9 8,4 11,0 9,0	0,189 0,176 0,216 0,189	0,146 0,133 0,173 0,146

Приведенные годовые затраты на строительство 1 м трубопровода составляют

.

Найдя первую производную от пои приравняв ее нулю, получим общее выражение для, удовлетворяющего минимуму приведенных годовых затрат,

.

Отсюда

. (13.27)

Рис.13.8

Здесь был показан принципиальный гидравлический подход к определению экономически наивыгоднейшего диаметра одиночного нагнетательного трубопровода.

Задача об определении может быть решена либо аналитически, либо подбором. Задаваясь различными значениями диаметра нагнетательной линии, находят соответствующие значенияи строят график (рис. 13.8). Экономически наивыгоднейший диаметр соответствует минимуму приведенных годовых затрат.