Глава 13

ГИДРАВЛИЧЕСКИЕ РАСЧЕТЫ ТРУБОПРОВОДОВ ПРИ УСТАНОВИВШЕМСЯ НАПОРНОМ ДВИЖЕНИИ ЖИДКОСТИ

13.1. Расчет простых трубопроводов

Простой трубопровод - трубопровод, не имеющий ответвлений, состоящий из труб одинакового диаметра, выполненных из одного материала. Движение жидкости в трубопроводе обусловлено напором, равным разности напоров в резервуарах - питателе и приемнике (рис. 13.1) или разности напоров в резервуаре-питателе и в струе на выходе из трубы (рис. 13.2), если резервуар-приемник отсутствует. Если указанная разность напоров не будет изменяться во времени, то движение установившееся.

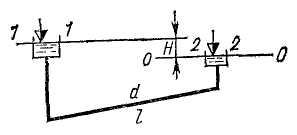
Рис. 13.1 Рис. 13.2

На различных участках трубопровода движение жидкости может быть равномерным и неравномерным (участки вблизи конструктивных элементов, обусловливающих появление местных сопротивлений, и участки стабилизации). На каждом из участков происходит потеря части напора.

По соотношению напоров, потерянных (затраченных на преодоление сопротивлений движению жидкости) на участках равномерного и неравномерного движения, простые трубопроводы делятся на длинные и короткие.

В гидравлически длинном (или просто длинном) трубопроводе потери напора по длине настолько превышают местные потери и скоростной напор, что сумму не вычисляют, а принимают как некоторую часть потерь по длине.

При расчетах длинных трубопроводов находят потери напора по длине , а затем суммарные местные потери напора учитывают, увеличивая найденные значенияна 5-10 %.

В коротком трубопроводе потери напора по длине и местные потери сопоставимы по значению. При гидравлическом расчете коротких трубопроводов учитываются как местные потери напора, так и потери напора по длине, а в балансе напоров учитываются скоростные напоры в сечениях потока.

По определяемым величинам и методике расчета простых трубопроводов задачи делятся на три группы:

1) определение расхода при заданном напоре, известной длине трубыи шероховатости стенок трубы, а также плотностии вязкости жидкости;

2) определение напора при заданном расходеи при известных длине, диаметре и шероховатости трубы, а также плотности и вязкости жидкости;

3) определение необходимого диаметра трубы при заданных расходе и напореи известных длине и шероховатости трубы, а также плотности и вязкости жидкости.

Каждая задача решается с помощью уравнения Бернулли и уравнения неразрывности.

13.2. Расчет длинного трубопровода постоянного диаметра

Для решения любой из поставленных выше задач составляется уравнение Бернулли для сечений 1-1 и 2-2 (рис. 13.1 и 13.2). Пренебрегая местными потерями и скоростными напорами, получаем

.

Выразим потери напора через гидравлический уклон , откуда

. (13.1)

Подставив (13.1) в формулу Шези , получим

. (13.2)

Решая уравнение относительно , имеем

. (13.3)

Расход жидкости при равномерном движении равен

. (13.4)

Объединив величины, зависящие от размеров (диаметра) трубы, представим их в виде так называемой расходной характеристики (модуля расхода)

. (13.5)

Расходная характеристика представляет собой расход в данной трубе при гидравлическом уклоне, равном единице. Получим

; (13.6)

. (13.7)

Напомним, что при равномерном движении гидравлический и пьезометрический уклоны равны.

Пренебрегая скоростным напором, получим, что линия удельной энергии (напорная линия) и пьезометрическая линия совпадают.

Ясно, что расход и расходная характеристикадолжны быть выражены в одних и тех же единицах.

Для вычисления напора запишем следующую формулу:

, (13 8)

где

(13.9)

- удельное сопротивление трубопровода.

Удельное сопротивление трубопровода численно равно напору, затрачиваемому на единице длины трубопровода при расходе, равном единице. Раскрывая значение в (13 9), с учетом того, что, получим

при =9,81 м/с².

По выведенным формулам решаются основные задачи при расчетах простого трубопровода.

Неновые стальные и чугунные трубы, т. е. бывшие в эксплуатации при нормальных условиях («нормальные» трубы), имеют повышенную шероховатость стенок, оценивавмую в среднем высотой выступа условной равнозернистой («эквивалентной») шероховатости 1,0-1,5 мм.

Новые чугунные трубы характеризуются средним значением 0,5 мм; новые стальные трубы имеют средние значения0,45 мм. При защитных покрытиях внутренней поверхности новых труб (битумизация, покрытие лаками и т.п.) шероховатость оценивается другими значениями.

Таблица 13.1

Вид труб	Скорость , м/с, при диаметре труб, мм
	50	100	200	300	400	500	600	1000	1400
Новые стальные	2,8	3,2	3,5	3,7	3,8	3,9	4,0	4,2	4,4
Новые чугунные	2,5	2,8	3,1	3,3	3,4	3,5	3,6	3,8	4,0
«Нормальные» (бывшие в эксплуатации)	0,8	0,9	1,0	1,1	1,1	1,2	1,2	1,3	1,3

С использованием значения для начала квадратичной области по (8.46) и указанных значенийнайдены значения, при превышении которых наступает квадратичная область (табл. 13.1); для «нормальных» труб здесь принято1,35 мм.

При турбулентном режиме движения отношение коэффициента Шези в квадратичной области к коэффициенту Шезив переходной области, обозначенное, согласно исследованиям Ф. А. Шевелева для каждого вида труб зависит только от средней скорости (при условии, если принять кинематическую вязкость жидкости=const).

Исходя из того что

,

имеем

.

Коэффициент .

Значения коэффициентов идля новых стальных и чугунных труб, а также для «нормальных» труб приводятся в справочниках.

Так как , ато

,

где - расходная характеристика в квадратичной области сопротивления;- расходная характеристика, в том числе и в переходной области.

Отсюда расход жидкости определится по формуле

. (13.10)

Из (13.7) с учетом (13.10) получим

. (13.11)

При расчете трубопроводов достаточно большой протяженности часто формулу (13.11) применяют в виде

, (13.12)

где - длина трубопровода, км. Следует помнить, что при расчетах дляинеобходимо применять одинаковые единицы величин.

Расходные характеристики подсчитаны И. И. Агроскиным с учетом предложенной им формулы (8.50) для коэффициента Шези.

В квадратичной области сопротивления . В переходной области сопротивления, а.

В соответствии с (13.10) получаем, что при движении жидкости в переходной области сопротивления при неизменных ирасходбудет меньше, чем в квадратичной области сопротивления.

Рассмотрим зависимость потерь напора в квадратичной области от диаметра трубопровода. Так как расходная характеристика , то, принявполучим из (13.11) при. Припотери напора обратно пропорциональны.

Это обязательно следует учитывать при проектировании трубопроводов. При неизменных остальных величинах в квадратичной области уменьшение диаметра в 1,5 раза приведет к увеличению потерь примерно в 8,7 раза, а уменьшение диаметра труб в 2 раза вызовет увеличение потерь напора уже примерно в 40 раз.