Глава 4

ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ

4.1. Напряженное состояние

ДВИЖУЩЕЙСЯ НЕВЯЗКОЙ ЖИДКОСТИ

Динамика жидкости - раздел гидромеханики, который изучает законы движения жидкостей в зависимости от приложенных к ним сил.

При заданных внешних силах задача динамики жидкости сводится к определению напряжений и кинематических параметров движения в каждой точке жидкости в любой момент времени, а также к определению гидродинамических сил воздействия потока на тела.

При движении невязкой жидкости не возникают силы внутреннего трения, а значит, в потоке нет касательных напряжений.

Нормальные напряжения в движущейся невязкой жидкости обладают теми же свойствами, что и в покоящейся жидкости, т. е. в данной точке их значения не зависят от направления действия. Таким образом, напряженное состояние движущейся невязкой жидкости может быть охарактеризовано в каждой точке значением нормального напряжения. Поскольку это значение не зависит от направления действия, его, как и при равновесии жидкости, называют давлением.

Невязкая жидкость - это модель жидкости, т. е. идеализированная среда, не встречающаяся в природе и технике. Однако изучение законов динамики этой идеализированной среды имеет большое значение. При решении некоторых задач применение законов движения невязкой жидкости для расчета реальных явлений дает результаты, достаточно точно описывающие реальное явление (например, при обтекании тел вытянутой плавной формы - крыла, лопасти рабочего колеса турбины). Кроме того, уравнения динамики невязкой жидкости в некоторых случаях служат исходными для получения уравнений движения вязкой жидкости.

4.2. Дифференциальные уравнения движения

НЕВЯЗКОЙ ЖИДКОСТИ (УРАВНЕНИЯ ЭЙЛЕРА)

Рассмотрим движущуюся невязкую жидкость, у которой плотность . Выделим в ней элементарный параллелепипед с ребрамипараллельными координатным осям (рис. 4.1). На массу жидкости в объеме параллелепипеда, равную, действуют массовые силы, пропорциональные массе, и поверхностные силы давления окружающей жидкости, распределенные по граням параллелепипеда, направленные по внутренним нормалям к граням и пропорциональные площадям соответствующих граней.

Рис. 4.1

Составим уравнения движения выделенной массы в проекциях на координатные оси.

Произведение массы жидкости в параллелепипеде на проекцию ускорения движения его центра масс (полюса) на направление ОХ равно

,

где - скорость центра масс в направленииX.

Проекция на направление ОХ массовых сил, действующих на выделенную массу жидкости, равна

,

где - проекция на ось ОХ плотности распределения массовой силы.

Чтобы записать проекцию сил давления на ось ОХ, вспомним, что в сплошной жидкой среде давление есть непрерывная функция координат точек жидкости и времени .

Обозначим давление в произвольной точке с координатамина левой вертикальной грани. В силу сплошности жидкости и непрерывности функции давленияна правой грани в точке с координатамидавление равноточностью до бесконечно малых второго порядка.

Разность давлений будет одинаковой для любой пары выбранных на гранях точек с одинаковыми координатамии, при этом проекция на осьОХ результирующей силы давления равна

.

Записав уравнение движения в направлении ОХ, получим

или после деления на массу

Аналогично можно получить уравнения движения в проекциях на направления осей OY и OZ:

Таким образом, система дифференциальных уравнений движения невязкой жидкости имеет вид

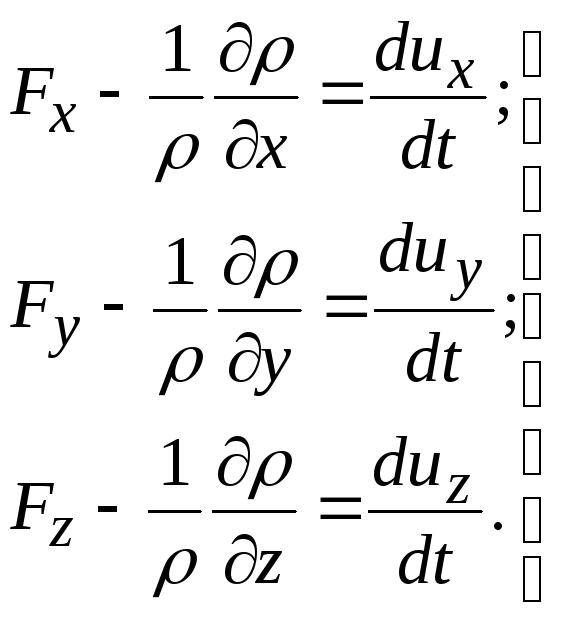(4.1)

Эти дифференциальные уравнения были впервые получены действительным членом Петербургской Академии наук Л. Эйлером в 1755 г.

Учитывая, что для неустановившегося движения компоненты (проекции) скорости и являются функциями времени, можно записать ускорения выделенной массы в развернутом виде:

Так как

уравнения Эйлера (4.1) можно переписать в виде

(4.2)

Для случая покоящейся жидкости уравнения (4.1) совпадут с дифференциальными уравнениями равновесия жидкости (2.4).

Уравнение движения невязкой жидкости вдоль линии тока имеет вид

, (4.3)

где - проекция плотности распределения массовых сил на направление касательной к линии тока;- ускорение частицы.

Уравнение (4.3) после преобразований имеет вид

или

. (4.4)

В задачах динамики жидкости массовые силы обычно считаются заданными (известными). Неизвестными являются функции давления , проекции скоростии плотность- всего пять неизвестных функций.

Для определения неизвестных переменных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений, к системе Эйлера добавляют уравнение неразрывности и уравнение состояния среды.

Для несжимаемой жидкости уравнение состояния const и уравнение неразрывности