2.3. Силы давления покоящейся жидкости на цилиндрические стенки

Рассмотрим некоторую ограниченную часть твердой цилиндрической поверхности, которую назовем цилиндрической стенкой. Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости, которое сводится к тому, что в каждой точке на стенку действует давление жидкости. Разобьем стенку на элементарные площадки. В силу малости площадок будем считать их плоскими и выразим элементарную силу давления на них в общем виде . Силыуже не будут направлены параллельно друг другу, их линии действия могут не пересекаться в одной точке, и их сумма может не сводиться к одной равнодействующей.

Рис. 2 13

Для шаровой или круговой цилиндрической стенки элементарные силы давления, будучи нормальными к элементарным площадкам на этих поверхностях, направлены по радиусам и, следовательно, пересекутся в центре сферы или в центре круга (поперечного сечения цилиндра).

Определение сил давления на цилиндрические и шаровые поверхности имеет важное значение, так как в гидротехнических сооружениях обычно применяются конструкции с такими поверхностями (секторные, сегментные, вальцовые и шаровые затворы, водонапорные баки и т. п.).

Рассмотрим цилиндрические стенки, находящиеся под односторонним воздействием покоящейся жидкости. Определим силу избыточного давления. При этом условимся одну из осей координат направлять вдоль образующей цилиндрической поверхности.

Цилиндрическая поверхность с горизонтальной образующей. Направим ось OY параллельно образующей (рис. 2.13), а ось OZ - вертикально вверх.

Значение силы давления на цилиндрическую поверхность в данном случае определяется следующим образом:

, (2.40)

где и- горизонтальная и вертикальная составляющие силы давления.

Выделим на цилиндрической поверхности элементарную площадку на которую действует направленная по нормали элементарная сила. Найдем горизонтальнуюи вертикальнуюсоставляющие силы:

;

.

Учитывая, что

и

имеем

;

,

где - проекция элементарной площадкина плоскость, перпендикулярную осиOX; - проекция элементарной площадкина плоскость, перпендикулярную осиOZ.

Проинтегрировав, получим для горизонтальной составляющей силы

, (2.41)

где - проекция всей цилиндрической поверхности на плоскость, нормальную к осиOX; - глубина центра тяжести проекциипод пьезометрической плоскостью.

Для вертикальной составляющей получим

.

Интеграл представляет собой объем призмы, ограниченной снизу цилиндрической поверхностью, а сверху - ее проекциейна пьезометрическую плоскость. Направляющие этой призмы - вертикальные прямые. Полученное таким образом тело называется телом давления.

Вертикальная составляющая численно равна весу жидкости в объеме тела давления:

, (2.42)

где объем тела давления. На рис. 2.13 тело давления заштриховано вертикальными линиями.

Горизонтальная составляющая проходит через центр давления проекции, а вертикальная составляющаяпроходит через центр тяжести тела давления.

Направление вертикальной составляющей для схемы, изображенной на рис. 2.13, а, - вниз, а на рис. 2.13, б - вверх.

Из рис. 2.13, а видно, что при построении тела давления криволинейная (в данном случае цилиндрическая) поверхность проектируется на свободную поверхность (рис. 2.13, а) или на ее продолжение (рис. 2.13, б). В первом случае жидкость заполняет тело давления, вертикальная составляющая направлена вниз; во втором случае жидкость не заполняет тело давления, и вертикальная составляющая силы давления направлена вверх.

Направление линии действия силы определяется направляющими косинусами

; (2.43)

. (2.44)

Цилиндрическая стенка с вертикальной образующей.

Направим ось OZ параллельно образующей цилиндра, а оси ОХ и OY расположим в горизонтальной плоскости. На плоскость, нормальную оси OZ, цилиндрическая поверхность проектируется в виде линии, т. е. =0. Тогда

(2.45)

Направление линии действия силы определятся направляющими косинусами

;

.

Рис.2.14

Для цилиндрической поверхности в виде четверти боковой поверхности цилиндра радиусом г и высотой h с вертикальной образующей (рис. 2.14)

Прямолинейная труба круглого поперечного сечения с вертикальной осью заполнена покоящейся жидкостью под постоянным давлением. Пусть ось трубы расположена вертикально. Найдем силу, действующую на стенки трубы (рис. 2.15).

Рис.2.15

Горизонтальная сила , стремящаяся разорвать трубу по вертикальному диаметральному сечению, при давлениибудет равна

,

где - длина трубы.

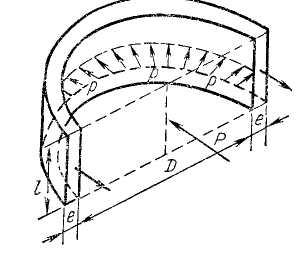
Рис.2.16

Эта сила действует на трубу как растягивающая. Она уравновешивается силами сопротивления, возникающими в материале, из которого изготовлена труба. Сила сопротивления распределена по площади осевого сечения трубы где- толщина стенки. Нормальное напряжение в материале стенок трубы определится при этом по формуле Мариотта

(2.46)

Произвольная криволинейная стенка abcd (рис. 2.16). В этом случае составляющие силы по направлениям горизонтальных осейОХ и OY (и) и вертикальной осиOZ () не равны нулю:

(2.47)

Если линии действия составляющих пересекаются, то воздействие жидкости сводится к одной силе . Линия действия силыопределяется углами, образованными направлениеми направлениями координатных осей. Косинусы этих углов вычисляются по соотношениям

;

.