2.4. Равновесие однородной несжимаемой жидкости относительно земли

Основное уравнение гидростатики. Рассмотрим жидкость, покоящуюся в сосуде, неподвижном относительно Земли. Для рассматриваемого случая действующей на жидкость массовой силой является только сила тяжести . Тогда.

Направив ось OZ вертикально вверх, получим

,

а подставив полученные величины в (2.5), будем иметь

. (2.12)

Интегрируя (2.12) в предположении =const и принимая, что в пределах рассматриваемого объема жидкости можно пренебречь изменением ускорения свободного падения по высоте (=const), получаем

или

, (2.13)

где - произвольная постоянная.

Разделив (2.13) на , получим

=const. (2.13а)

При делении на уравнение (2.13) примет вид

= const. (2.14)

Отметим, что члены уравнения (2.13а) отнесены к единице веса, а (2.14) - к единице массы.

Для двух точек одного и того же объема покоящейся жидкости уравнения (2.13а) и (2.14) представляются в виде

; (2.15)

. (2.16)

Уравнения (2.15) и (2.16) выражают гидростатический закон распределения давления в однородной несжимаемой жидкости, покоящейся относительно Земли. Уравнение (2.15) обычно называют основным уравнением гидростатики.

Поверхности равного давления. Для рассматриваемого случая равновесия, когда единственной массовой силой, действующей на жидкость, является сила тяжести, поверхности равного давления =const представляют собой семейство горизонтальных плоскостей.

Действительно, из (2.12) при получаем, т. е.

(2.17)

Каждому значению соответствует плоскость, в точках которой давление имеет определенное постоянное значение. Свободная поверхность жидкости в данном случае является одной из плоскостей равного давления. Здесь следует указать, что полученный вывод справедлив лишь в пределах сравнительно небольших поверхностей, для которых можно считать вектор ускорения свободного падения вертикальным.

Если рассматривать массу жидкости, имеющей большую поверхность, например поверхность моря, то становится очевидным, что необходимо учитывав действительное направление вектора ускорения свободного падения (по радиусу к центру Земли), а также то, что поверхности равного давления (и в том числе свободная поверхность) в этом случае не будут горизонтальными. Основное уравнение гидростатики можно записать иначе. Рассмотрим жидкость, покоящуюся в открытом резервуаре (рис. 2.4).

Рис.2.4

Пусть необходимо определить давление в точкеА на уровне . Применим основное уравнение гидростатики (2.15) к точке и к точкеВ, расположенной на свободной поверхности жидкости на уровне . Давление на свободной поверхности равно, его называют внешним давлением. Оно может быть равным атмосферному (), большим () или меньшим () атмосферного.

Из основного уравнения гидростатики (2.15) имеем

.

Отсюда

(2.18)

где ;- глубина погружения точки под свободной поверхностью. Тогда

. (2.19)

Величину называют весовым давлением, так как она равна весу столба жидкости при единичной площади и высоте.

Таким образом, по (2.19) давление в точке покоящейся жидкости, находящейся на глубине под свободной поверхностью, равно сумме внешнего давленияи давления.

Иногда давление называют абсолютным давлением и обозначают.

Избыточное и вакуумметрическое давление. Избыточным давлением называют разность

. (2.20)

В гидротехнических сооружениях, как правило, на свободной поверхности жидкости давление равно атмосферному .

В этих случаях

, (2.21)

где - глубина погружения рассматриваемой точки под свободной поверхностью жидкости. Таким образом, приизбыточное и весовое давления совпадают.

Если давление в жидкости меньше атмосферного, то напряженное состояние жидкости характеризуется значением разрежения (вакуума).

Вакуумметрическое давление

. (2.22)

Давление измеряется с помощью пьезометров, манометров и вакуумметров.

Эпюры давления. Закон распределения в жидкости гидростатического давления легко изобразить графически в виде эпюр давления. Для этого нужно представить давление вектором, направление которого совпадает с направлением давления, а значение пропорционально значению давления.

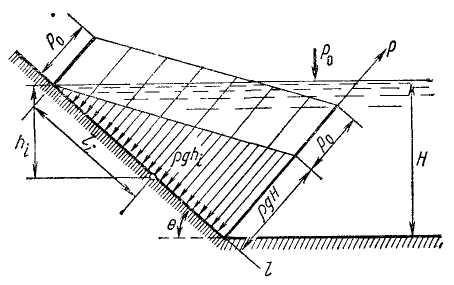
Рис. 2.5

Эпюры всегда следует строить со стороны жидкости, помня о направлении действия нормальных напряжений в покоящейся жидкости (по внутренней нормали). Так, для плоской наклонной стенки, восстановив в каждой ее точке перпендикуляры, равные для давления идля избыточного давления (при), и объединив концы этих отрезков, получим соответствующие эпюры давления (рис. 2.5);- глубина погружения рассматриваемойi-й точки под свободной поверхностью.

Закон Паскаля. Применив основное уравнение гидростатики к двум точкам покоящейся жидкости изменим давление в первой точке на, не нарушая равновесие жидкости. Тогда во второй точке давление должно измениться на некоторую величину. Из основного уравнения гидростатики следует, что

или

,

т. е. изменение давления в любой точке покоящейся жидкости передается в остальные ее точки без изменений. Это положение называется законом Паскаля.

Сообщающиеся сосуды. Допустим, что имеются два сообщающихся сосуда, содержащих жидкости с различными плотностями и(рис. 2.6). Сосуды открыты, и внешнее давление на их свободных поверхностях одинаково:. Поверхность раздела жидкостей, являясь поверхностью равного давления, будет горизонтальной плоскостью. Следовательно,. Отсюда

.

При разнородных жидкостях в открытых сообщающихся сосудах высоты уровней над плоскостью раздела жидкостей будут обратно пропорциональны плотностям жидкостей.