Глава 2

ГИДРОСТАТИКА

2.1. Напряженное состояние покоящейся жидкости. Гидростатическое давление

Рассмотрим массу жидкости, находящейся в состоянии покоя (рис.2.1) (в общем случае относительного покоя), когда жидкость в резервуаре, который движется с ускорением относительно Земли, неподвижна по отношению к резервуару.

Рис.2.1

Рассечем объем, занимаемый жидкостью, произвольной плоскостью на две части, содержащие соответственно массы и, и отбросим одну из частей объема, например правую.

Чтобы сохранить равновесие оставшейся в левой части массы жидкости необходимо к ней приложить силу, эквивалентную действию отброшенной массы. Эта сила должна быть распределенной по площади рассечения. Напряжение этой силы в произвольной точкеА площади со определяется соотношением

, (2.1)

где - элементарная площадка на площади рассечения, содержащая произвольную точкуА; - сила, действующая на площадку. При предельном переходе площадкастягивается в точкуА.

Покажем, что сила и напряжениенаправлены по внутренней нормали к площадке. Действительно, если бы силабыла направлена не по нормали к площадке, то эту силу можно было бы разложить на составляющие: нормальную и касательную к площадке. Из-за текучести жидкости касательная составляющая привела бы жидкость в движение, т. е. в этом случае равновесие жидкости было бы невозможно.

Так как жидкость не сопротивляется растягивающим усилиям, то сила может быть только сжимающей. Таким образом, по любой поверхности, проведенной внутри покоящейся жидкости, всегда действует только распределенная сжимающая сила.

Нормальное напряжение поверхностных сил в покоящейся жидкости направлено всегда по внутренней нормали к площадке действия.

Через произвольную точку A покоящейся жидкости можно провести бесчисленное множество секущих поверхностей, по-разному ориентированных в пространстве. На любой из них можно выбрать площадку , содержащую точкуА, и вычислить нормальное напряжение .

При этом всегда направлено по внутренней нормали к площадке, т. е. направлениезависит от того, на какой из секущих поверхностей выбрана площадка.

Докажем, что в покоящейся жидкости значение нормального напряжения не зависит от ориентации . Для этого выделим в покоящейся жидкости элементарную частицу в форме тетраэдра с ребрами, выбранными вдоль координатных осей, и объемом(рис. 2.2).

Три грани тетраэдра лежат в координатных плоскостях, а четвертая граньнаклонна и ориентирована нормально к направлению.

Отбросим окружающую тетраэдр жидкость и для сохранения равновесия выделенной частицы приложим к каждой грани тетраэдра поверхностные силы и.

Рис.2.2

Кроме поверхностных сил на жидкость, заключенную в тетраэдре, действует массовая сила , плотность распределения которой. Проекцияна оси координат обозначим.

Записав в проекциях на координатные оси уравнения равновесия жидкости, заключенной в тетраэдре, получим

или

Аналогично

(2.2)

и

В уравнениях (2.2) обозначения 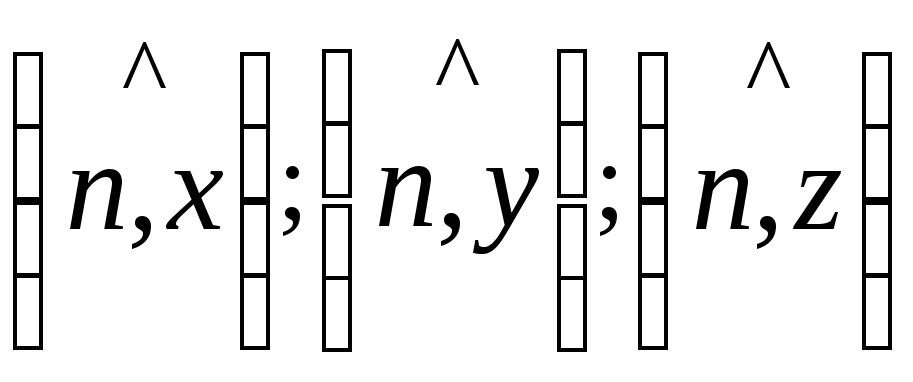относятся к углам, образуемым нормалью к гранис осями координат.

Если разделить каждый из членов первого уравнения (2.2) на площадь то получим

Но - площадь грани, перпендикулярной осиОХ, т.е. грани ABD.

Так как объем тетраэдра , а площадь грани, то можно записать

.

Стягивая тетраэдр в точку A, в пределе получаем

.

Аналогично другие два уравнения в (2.2) дадут соответственно

и ,

откуда

.

Таким образом, доказано, что нормальное напряжение в любой точке покоящейся жидкости не зависит от направления действия. Это позволяет характеризовать напряженное состояние покоящейся жидкости в каждой точке скалярной величиной, представляющей значение нормального напряжения в этой точке. Эта величина называется гидростатическим давлением.

Давление может быть неодинаковым в различных точках покоящейся жидкости:

.